Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 13 из 37

Статистические гипотезы и их виды

Нулевая гипотеза (нуль-гипотеза) и альтернатива (альтернативнаягипотеза).

В спорте часто при анализе какого-либо явления приходится по неко- торым измерениям показателя делать обобщающий вывод. Например, по- сле тренировочного занятия 15 легкоатлетов у трех наблюдается неполное восстановление. Можно ли на этом основании судить о трудности трени- ровочного процесса или это случайность? Наверное, если такой неприят- ный факт случится со всеми 15 спортсменами, сомнений в неправильном построении занятия не будет. Следовательно, в данном случае можно го- ворить о представительности (репрезентативности) выборки, на основа- нии которой можно сделать вывод. Этот же вопрос можно сформулиро- вать иначе: сколько испытуемых необходимо обследовать, чтобы полу- чить достоверные результаты измерений? Это очень важно исследовате- лям, так как является необходимостью научно решаемых задач. А так как почти во всех случаях выборочного наблюдения параметры генеральной совокупности остаются неизвестными, то о них приходится судить по вы- борочным данным, т. е. гипотетически, так как выборочные показатели яв- ляются величинами случайными. Поэтому такие вопросы, как сравнение результатов различных групп, оценка точности результатов измерений,

оценка достоверности коэффициентов взаимосвязи и другие, решаются с использованием некоторых приемов проверки статистических гипотез.

Статистическойгипотезой(илипростогипотезой)называетсяпро-веряемое математическими методами предположение о виде неизвест-ногораспределения,илиопараметрахизвестныхраспределений.

Например, статистическими являются гипотезы:

1. 
   генеральная совокупность распределена по закону Пауссона;
   
2. 
   дисперсии двух нормальных совокупностей равны между собой. Эти две различные статистические гипотезы. В первой гипотезе сде-
   

лано предположение о виде неизвестного распределения, во второй – о параметрах двух известных распределений. Гипотезы предстоит прове- рить с помощью какого-то метода – критерия.

Статистические гипотезы обычно рассматривают две генеральные со- вокупности, одна из которых может представлять собой теоретическую модель (например, нормальное распределение), а о второй судят по вы- борке из нее. В других случаях обе генеральные совокупности представ- лены выборками.

Для оценки величины генеральных параметров по выборочным пока- зателям используется нулевая(основная)гипотеза,или нуль-гипотеза, т. е. предположение о том, что генеральные параметры, о которых судят по выборочным данным, не отличаются друг от друга, и что разница, наблюдаемая между выборочными показателями, носит не систематиче- ский, а исключительно случайный характер. Обратное нуль-гипотезе утверждение о том, что в действительности между генеральными сово- купностями есть различия, называется альтернативной (противополож-ной)гипотезойили альтернативой.

Итак, вначале выдвигается нулевая гипотеза о том, что различия между генеральными совокупностями равно нулю. Затем получают вы- борку или несколько выборок, и если выборочные данные не противоре- чат нулевой гипотезе, т. е. различия можно объяснить только случайно- стью выборки, то нулевая гипотеза принимается. Если же полученные ре- зультаты не удается объяснить только воздействием случайных факторов, то нулевая гипотеза отвергается, а принимается альтернативная гипотеза. Нулевую гипотезу принято обозначать, как Н₀, а альтернативную – Н₁.

Например, при оценке эффективности применения нового метода тре- нировки юных спортсменов–спринтеров по среднему значению спортив- ного результата в контрольной и экспериментальной группах, нулевую гипотезу можно сформулировать следующим образом: средние значение результатов в группах не изменилось, т. е. x̄₁ = x̄₂. Для краткости это за- писывается так: H₀: x̄₁ = x̄₂.

Если же заранее нельзя сказать, к чему приведет применение новой методики тренировки – к увеличению или снижению результатов, то аль- тернативная гипотеза Н₁ будет состоять в том, что средние значения гене- ральных совокупностей неодинаковы: H₁: x̄₁ G x̄₂.

Ошибкиприпроверкегипотез.

При сравнении статистических характеристик почти никогда не встре- чается случая их абсолютного равенства. В силу каких-то случайных или закономерных причин значения их отличаются друг от друга. Задача при

проверке гипотез состоит в том, чтобы отличить случайные влияния от закономерных.

При проверке статистической гипотезы решение экспериментатора никогда не принимается с уверенностью, т.е. всегда существует некото- рый риск принять неправильное решение. Оценка степени этого риска и представляет собой суть проверки статистической гипотезы. Ясно, что ис- ключить на 100% этот риск невозможно. Но экспериментатор может вы- брать вероятность, или уровень значимости, который характеризует ве- роятность отклонения, признаваемого невозможным в силу лишь случай- ных причин. Самыми распространенными уровнями являются: 0,001; 0,01; 0,05. Уровень 0,05 означает, что выборочное значение может встре- титься в среднем не чаще чем 5 раз в 100 наблюдениях.

Ошибки, допускаемые при проверке гипотез, удобно разделить на два вида: 1) отклонение гипотезы Н₀, когда она верна, – ошибкапервогорода;

2. 
   принятие гипотезы Н₀, когда в действительности верна какая-то другая гипотеза, – ошибка второгорода.
   

Вероятность ошибки первого рода обозначается . Величина  назы- вается уровнем значимости критерия, по которому проверяется справед- ливость гипотезы Н₀.

Вероятность ошибки второго рода обозначается , которую принято называть доверительной вероятностью. Её величина зависит от альтер- нативной гипотеза Н₁ (при уровне значимости 0,05 доверительная вероят- ность равна 0,95 и т.п.). Отсюда, опираясь на теорему суммы вероятностей противоположных событий, вытекает, что  +  = 1.

Вероятности  и  удобно представить, как это сделано в таблице 2.2.1.

Таблица 2.2.1

Ошибки при проверке гипотез

	Решение
	Принятие Н0	Принятие Н1
Справедлива Н0	Правильное с вероятностью 1 – 	Ошибочное с вероятно- стью 
Справедлива Н1	Ошибочное с вероятно- стью 	Правильное с вероятностью 1 – 

Наглядным способом интерпретации ошибок является их графическое представление.

Предположим, что проверяется гипотеза Н₀:  = ₀ о равенстве сред- него значения генеральной совокупности и заданной величине ₀.

Для этого берется выборка объема n, находится её среднее арифмети- ческое x̄и по его величине судят о справедливости гипотезы Н₀.

Распределение среднего арифметического x̄ при условии, что верна гипотеза Н₀, буде f(x̄/μ₀). Это распределение чисто качественно пред- ставлено на рисунке 2.2.1.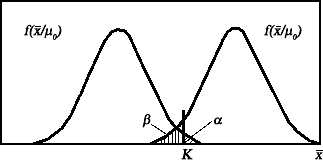


Рис. 2.2.1. Ошибки первого и второго рода

Распределение среднего арифметического x̄ при условии, что верна альтернативная гипотеза Н1:  = 1, будет уже другим – f(x̄/μ₁).

Будем считать, что гипотеза Н0 отвергается, если выборочное среднее арифметическое x̄ окажется больше некоторого значения К, т. е. x̄ > K, как показано на рисунке 2.2.1.

Область непринятия гипотезы Н₀ называется критической областьюкритерия. Она показана на рисунке 2.2.1. наклонной штриховкой. Уро- вень значимости будет соответствовать площади критической области.

Вероятность ошибки второго рода  будет равна площади под кривой распределения f(x̄/μ₁), показанной вертикальной штриховкой.

Величин 1 –  называется мощностьюкритерия,т.е. вероятность того, что не будет допущена ошибка второго рода.

При этом необходимо помнить, что единственный способ одновремен- ного уменьшения вероятностей ошибок первого и второго рода при дока- зательстве гипотез состоит в увеличении объема выборок.

Следует особо подчеркнуть, что любая гипотеза должна формулиро-ваться,ауровеньзначимости задаватьсяисследователемвсегдадопо-лучения экспериментальных данных, по которым эта гипотеза будетпроверяться.

Отсюда следует, что как принятие, так и отклонение гипотезы осу- ществляется на основе определенного критерия. Статистическим кри-терием называют правило, обеспечивающее принятие истинной или от- клонение ложной гипотезы с заранее заданной вероятностью.

Таким образом, систематизирую все сказанное, запишем основные этапы проверки гипотезы:

1. 
   Формулировка гипотезы (нуль-гипотезы), которую в дальнейшем необходимо принять или отклонить.
   
2. 
   Выбор уровня значимости.
   
3. 
   Определение выборочного значения статистических характеристик
   

(на основе измерения или наблюдения выборочной совокупности).

4. 
   Выбор критерия для проверки статистической гипотезы.
   
5. 
   Сравнение расчетного значения с критическим значением критерия для выбранного уровня значимости и принятие или отклонение гипотезы.
   

Критериизначимости.

Методы, с помощью которых для каждой выборки формально точно определяются, удовлетворяют ли выборочные данные нулевой гипотезе или нет, называются критериямизначимости.

Процедура проверки гипотез обычно сводится к тому, что по выбороч- ным данным вычисляется значение некоторой величины, называемой статистикойкритерия, или просто критерием, который имеет извест- ное стандартное распределение (нормальное, t-распределение Стьюдента и т. п.). Найденное значение критерия сравнивается с критическим (гра- ничным) значением критерия, взятым из соответствующих таблиц, и по результатам сравнения делается вывод: принять гипотезу или отвергнуть. Если вычисленное по выборке значение критерия не превосходит гра- ничного значения, то гипотеза Н₀ принимается на заданном уровне значи- мости . В этом случае наблюдаемое по экспериментальным данным раз- личие генеральных совокупностей можно объяснить только случайно- стью выборки. Однако принятие гипотезы Н₀ совсем не означает доказа- тельства равенства параметров генеральных совокупностей. Просто име- ющийся в распоряжении статистический материал не дает оснований для отклонения гипотезы о том, что эти параметры одинаковы. Возможно, по- явится другой экспериментальный материал, на основании которого эта

гипотеза будет отклонена.

Когда вычисленное значение критерия оказывается больше гранич- ного (критического) значения при заданном уровне значимости , то наблюдаемое различие генеральных совокупностей уже нельзя объяснить только случайностями. В этом случае гипотеза Н₀ отклоняется в пользу гипотезы Н₁ при данном уровне значимости , и говорят, что наблюдае- мое различие значимо(статистическизначимо) на уровне значимости .

Следует подчеркнуть разницу между статистической значимостьюи практической значимостью. Заключение о практической значимости всегда делается человеком, изучающим данное явление. И здесь истин- ным критерием является опыт и интуиция исследователя, а статистиче-ские критерии значимости – лишь формально точный инструмент, ис-пользуемый в исследовании. Чем больше исследователь знает об изучае- мом явлении, тем точнее будет сформулированная им гипотеза, и тем точ- нее будут выводы, сделанные с помощью критериев значимости.

Ранее уже подчеркивалось, что уровень значимости  должен выби- раться исследователем до получения экспериментальных данных, по ко- торым будет проверяться гипотеза. Но часто с предварительным выбором возникают затруднения. Обычно говорят, что для научных исследований (в том числе и в спорте) достаточен уровень значимости  = 0,05, но если выводы, которые предстоит сделать по результатам проверки гипотез, связаны с большой ответственностью, то рекомендуется выбирать  =0,01 или  = 0,001.

Критерии значимости подразделяются на три типа:

1. 
   Критерии значимости, которые служат для проверки гипотез о па- раметрах распределений генеральной совокупности (чаще всего нормаль- ного распределения). Эти критерии называются параметрическими.
   
2. 
   Критерии, которые для проверки гипотез не используют предполо- жений о распределении генеральной совокупности. Эти критерии не тре- буют знания параметров распределений, поэтому называются непарамет-рическими.
   
3. 
   Особую группу критериев составляют критерии согласия, служа- щие для проверки гипотез о согласии распределения генеральной сово- купности, из которой получена выборка, с ранее принятой теоретической моделью (чаще всего нормальным распределением).
   

В спортивной практике при проведении исследований необходимо также учитывать, что различия сравниваемых параметров может быть как положительным, так и отрицательным. Поэтому, выбирая критерии зна- чимости, необходимо учитывать тот факт, что ни могут быть двусторон- ними и односторонними.

Если цель исследования состоит в том, чтобы выявить различие пара- метров двух генеральных совокупностей, и при этом часто неизвестно, ка- кой из этих параметров будет больше, а какой меньше, то применяется двусторонняя гипотеза, допускающая, что различие может быть любого знака. При этом нулевая гипотеза состоит в том, что дисперсии совокуп-

ностей равны между собой (H₀: σ² = σ²), а цель – исследования доказать

^{1 2} 2 2

наличие различия между дисперсиями (H₁: σ₁ G σ₂ ).

Если же цель исследования состоит в том, чтобы доказать увеличение или уменьшение отдельного параметра (например, средний результат в экспериментальной группе выше, чем в контрольной), и при этом не до- пускается, что различие может быть другого знака, то применяются одно- сторонние гипотезы. При этом альтернативная гипотеза H₁: μ₂ > μ₁ (или H₁: μ₂ < μ₁), а обратное ей утверждение H₀: μ₂ ≤ μ₁ (илиH₀: μ₂ ≥ μ₁).

Критерии значимости, служащие для проверки двусторонних гипотез, называются двусторонними, а для односторонних – односторонними.

При этом необходимо помнить, что ни в коем случае нельзя выбиратьтот или иной критерий после проведения эксперимента на основе ана-лиза экспериментальных данных, поскольку это может привести к не-вернымвыводам. И если имеются основания для применения односторон- него критерия, его следует предпочесть двустороннему, потому что одно- сторонний критерий полнее использует информацию об изучаемом явле- нии и поэтому чаще дает правильные результаты.

Критерии, основанные на нормальном распределении.Сравнениедвухвыборочныхсредних.t-критерияСтьюдента

Из параметрических критериев при сравнении средних величин глав-

ным образом применяется t-критерий Стьюдента.


√
Английский биометрик Вильям Госсет (1908), печатающий под псев- донимом Стьюдент (Student), исследуя закон распределения малой вы- борки (n< 30), впервые установил, что выборочная случайная величина

t = ^x–μ ⋅ n имеет непрерывную функцию распределения (для - < t< +)

σ

с плотностью, под которой понимается число случаев, приходящихся на единицу ширины классового интервала непрерывно варьирующего при- знака (отношение частоты данного интервала к его ширине, выраженное в единицах измерения вариант данного ряда), равной:

f(t) = C_n–1
n

(1+ ^t2 )², (2.2.1)

n–1

где С– константа, зависящая только от числа степеней свободы n– 1.

Закон Стьюдента, в дальнейшем уточненный Р.Э. Фишером (1924), яв- ляется основой “теории малой выборки”. В соответствии с этим законом, если варианты генеральной совокупности распределены нормально, вели- чина tподчиняется так называемому t-распределению, которое не зависит от параметров генеральной совокупности  и , а определяется только числом степеней свободы f = n – 1. C увеличением числа наблюдений, t- распределение быстро приближается к нормальному.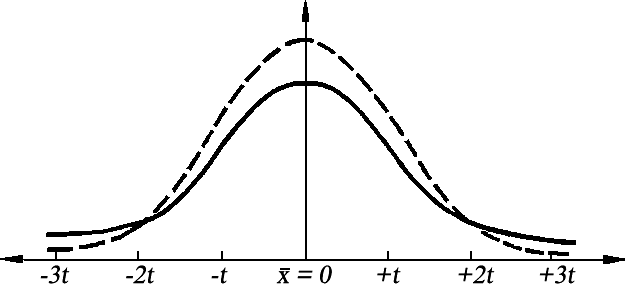

Более наглядное представление о t-распределении дает рисунок 2.2.2, где на фоне нормальной кривой нанесена (более плоская) кривая t-распре- деления при n= 3.

Рис. 2.2.2. T-критерий распределения при n = 3 (на фоне кривой нормальной кривой)

Отсюда следует, что t-распределение Стьюдента представляет част- ный случай нормального распределения, оно симметрично и отражает специфику распределения малой выборки по нормальному закону в зави- симости от ее объема n.

При сравнении данных двух выборок на основании расчета t-критерия Стьюдента могут представиться следующие случаи:

Группы по объему входящих в них данных могут быть: а) обе группы большие (n> 30);

б) обе группы малые (n 30);

в) одна – большая (n > 30), вторая – малая (n 30).

2. Группы по своему составу могут разделяться:

а) группы с зависимыми вариантами, когда i-тая варианта первой группы сравнивается с i-той вариантой второй группы (сравнение резуль- татов повторных тестирований одной и той же выборки, n_x=n_y) ;

б) группы с независимыми вариантами (можно менять варианты ме- стами внутри выборки, т.е. данные тестирования по одному и тому же по- казателю у разных групп).

Исходя из таких условий, задачи могут быть трех типов: сравнение двух больших (или одной большой, одной малой) групп с независимыми вариантами, сравнение двух малых групп с независимыми вариантами и сравнение двух малых или больших групп с зависимыми вариантами.

Здесь еще необходимо учесть, что при применении методов сравне- ния, основанных на расчете t-критерия, необходимо производить расчет числа степеней свободы. Под числом степеней свободы понимают раз-ность между числом измеряемых (наблюдаемых) значений и числом ли-нейныхотношений(связей),возникающихмеждуними. Это понятие также было более полно раскрыто Стьюдентом. Расчет степеней свободы производится по формуле:

k = n_x + n_y — 2, (2.2.2)

где n_x– объем выборки Х; n_y– объем выборки Y.

Число степеней свободы необходимо при сравнении расчетного значе- ния критерия с критическим (граничным) значением из статистических таблиц. При этом необходимо помнить, что все статистические таблицы содержат данные для различного числа степеней свободы. Поэтому при использовании каждого критерия надо правильно определять число сте- пеней свободы.

При сравнении двух больших (или одной большой, одной малой) группс независимыми вариантами применяется расчет t-критерия Стьюдента, основанный на предположении, что обе выборки, у которых наблюдаются различия в значениях средних величин, получены из одной генеральной совокупности, имеющей приближенно нормальное распределение, и, сле- довательно, значимо они не отличаются друг от друга. Сравнение прово- дится по формуле:

t = ^|x̄–ȳ|, (2.2.3),

√^m2_̄ ^+m2_̄

x y

где x̄, ȳ– величины средних выборок Хи Y;

m_x̄, m_ȳ – стандартные ошибки средних выборок Xи Y.

После того, как произведено вычисление значения t-критерия (t_фак), его необходимо сравнить с критическим значением (t_st). Для этого поль- зуются таблицей теоретического t-распределения Стьюдента (прил. 1) при заданном уровне значимости  и числе степеней свободы k. При этом если расчетное значение t-критерия меньше минимального табличного значе- ния (t_фак < t_st), то выборочные средние не различаются на уровне значи- мости . В противном случае (t_фак t_st) различие статистически значимо и необходимо отвергнуть предположение о том, что выборки взяты из од- ной генеральной совокупности.

Пример 2.2.1. При проведении тестирования школьников одной из школ крас- нодарского края необходимо было выявить, существуют ли возрастные различия в показателях ЖЕЛ у учащихся 11 и 12 лет. Предварительный расчет показал, что в группе Х(школьники 11 лет) среднегрупповой показатель ЖЕЛ был равен 2484 мл ⁽ⁿx^{= 60), а в группе Y(школьниики 12 лет) он составил 2696 мл (n}y^{= 62), а стандарт- ные ошибки средних значений были следующие: m}x^{=  37,7 мл, m}y^{=  51,7 мл.}

Решение.

1. 
   На основании данных средних величин выборок выдвигаем рабочую гипотезу. Рабочая гипотеза: т.к. x̄ = 2484 мл < ȳ = 2696 мл, то предположим, что по- казатели ЖЕЛ ниже в группе X(ученики 11 лет), чем в группе Y(ученики 12 лет).
   
2. 
   Сравнение данных выборок произведем, используя расчет t-критерия по формуле (9.3), предположив, что распределение результатов тестирования школь- ников по показателям ЖЕЛ в выборках с большими объемами (n >30) подчиняется закону нормального распределения:
   

_{Тогда t =}^|x̄–ȳ^| ₌ ^|2484–2696^|

≈ ²¹² ≈ 3,31.

√^m2_̄ ^+m2

√^{1421,29+2672,89}

63,99

x y

3. 
   Число степеней свободы в соответствии с формулой (2.2.2) равно:
   

k = n_x + n_y — 2 = 60 + 62 — 2 = 120.

4. 
   Сравниваем полученное значение t-критерия с табличным значением (при- ^{лож. 1) для k= 120. При  = 99% – t}st^{= 2,62, а при  = 99,9% – t}st^{= 3,37. Полученный} показатель выше второго порога доверительной вероятности, но ниже третьего.
   

^{Вывод:т.к. t}ф^{= 3,31 > t}st^{= 2,62, то различия в показателях ЖЕЛ у школьников}

11 и 12 лет достоверны по второму порогу доверительной вероятности ( = 99%).