Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 14 из 37

Пример 2.2.2. Данные психофизиологическое тестирование учеников одной из школ показали, что средний показатель времени ответа на каждый вопрос ком- ^{пьютерного теста в группе Х (n}x ^{= 50) составил 457 мс, а в группе Y он был равен 441 мс (n}y ^{= 54). Стандартные ошибки средних значений были следующие: m}x ^{=  6,6 мс, m}y^{=  6,8 мс. Необходимо определить достоверность различий между груп-} пами в показателях времени ответа при компьютерном тестировании.

Решение.

1. 
   На основании данных средних величин выборок выдвигаем рабочую гипотезу.
   

Рабочая гипотеза: т.к. x̄ = 457 мс > ȳ = 441 мс, то предположим, что в группе Xпоказатели времени ответа на каждый вопрос выше, чем в группе Y.

2. 
   Сравнение данных выборок произведем, используя расчет t-критерия по формуле (9.3) предположив, что распределение результатов времени ответа на каждый вопрос компьютерного тестирования в выборках с большими объемами (n >30) было нормальное:
   

_{Тогда t =}^|x̄–ȳ^| ₌ ^|457–441^|

_≈ 16

≈ 1,68.

√^m2_̄ ^+m2

√^43,56+46,24

9,48

x y

3. 
   Число степеней свободы в соответствии с формулой (2.2.2) равно:
   

k = n_x + n_y — 2 = 50 + 54 — 2 = 102.

4. 
   Сравниваем полученное значение t-критерия с табличным значением (при- лож. 1) для k= 100 . При этом полученный показатель меньше минимального таб- ^{личного значения t}st^{= 1,98 для  = 95%.}
   

^{Вывод: т.к. t}ф ^{= 1,68 < t}st ^{= 1,98 для k = 100 при  = 99%, то различия в показа-} телях у школьников 11 и 12 лет достоверны по второму порогу доверительной вероятности.

При сравнении двух малых групп с независимыми вариантами расчет t-критерия Стьюдента также основан на предположении, что обе выборки, у которых наблюдаются различия в значениях средних величин, досто- верно не различаются, если они получены из одной генеральной совокуп- ности. Сравнение проводится по формуле:

_{t =} |x̄–ȳ|⋅_√n_x⋅n_y⋅(n_x+n_y–2) _{. (2.2.4)}

⁽[ ∑(x_i–x̄)²+∑(y_i–ȳ )²]⋅(n_x+n_y)
После того как произведен расчет t-критерия Стьюдента и числа сте- пеней свободы по формуле (2.2.1), из таблицы t-критерия Стьюдента (при- лож. 1) находится критическое значение t-критерия для трех порогов до- верительной вероятности  и уровней значимости . В случае, если рас- четное значение t-критерия меньше минимального значения из таблицы (t_ф<t_st), то различия между данными двух выборок нельзя считать досто- верными, это предположение ошибочно, т. е. выборки примерно одина- ковы по избранному показателю. Если же t_ф t_st, т. е. расчетная величина t-критерия соответствует табличным данным или выше их, то говорят о достоверности различий при определенной степени доверительной веро- ятности  (или уровне значимости ) и числе степеней свободы k.

Пример 2.2.3. Проведено измерение показателей роста у двух групп исследу- емых. Определить достоверность различий методом Стьюдента в полученных ре- зультатах, если данные выборок таковы:

^xi^{, см 176; 180; 187; 172; 175; 190; 170; 191 (n}x<sup>= 8);

y</sup>i^{, см 180; 170; 162; 168; 165; 173; 175; 183; 180; 169 (n}y^{= 10).}

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и делаем необходимые расчеты.
   

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2
176	-4	16	180	8	64
180	0	0	170	-2	4
187	7	49	162	-10	100
172	-8	64	168	-4	16
175	-5	25	165	-7	49
190	10	100	173	1	1
170	-10	100	175	3	9
191	11	121	183	11	121
			180	8	64
			169	-3	9
x= 180		∑(xi — x̄)2= 475	y= 172		∑(yi — ȳ)2 = 437

На основании расчета средних величин выборок выдвигаем рабочую гипотезу.

Рабочаягипотеза:т.к. x̄ = 180см  ȳ = 172 см, то предположим, что в группе

Xисследуемые более высокорослы, чем группы Y.

3. 
   Подтвердим выдвинутое предположение расчетом величины t-критерия Стьюдента, используя формулу (2.2.4):
   

_{t =} ^{|180 — 172| ⋅} √^{8 ⋅ 10 ⋅ (8+ 10— 2)} ₌ ^8⋅ √¹²⁸⁰ _≈ ^{8 ⋅ 35,78} _{≈ 1,06}

^ф √^{(475 + 437) ⋅ (8 + 10)}

√⁷²⁹⁶⁰

270,11

3. 
   Рассчитаем число степеней свободы по формуле (2.2.2):
   

^{k= n}x^{+ n}y^{– 2 = 8 + 10 – 2 = 16.}

3. 
   ^{Сравнить расчетное значение t-критерия (t}ф ^{= 1,06) с табличным значением для k= 16 при}  ^{= 5% (} ^{= 95%) (прилож. 1) и сделаем вывод.}
   

^{Вывод:т.к. t}ф^{= 1,06  t}st^{= 2,12 для k= 16 при  = 95%, то различия в показа-}

телях роста двух групп исследуемых недостоверны, т.е. по данному параметру они примерно равные.

Пример 2.2.4. Проведено тестирование двух групп легкоатлетов в беге на 800 м. Определить достоверность различий методом Стьюдента в полученных резуль- татах, если данные выборок таковы:

^xi<sup>,с 117,0; 118,5; 120,0; 122,0; 120,0; 124,0; 124,5; 120,5; 121,0; 121,0; 122,0;

123,5; 123,5 (n</sup>x<sup>= 13).

y</sup>i<sup>,с 120,5; 122,0; 125,5; 126,0; 123,5; 129,5; 131,0; 124,0; 126,0; 125,0; 127,0;

129,0; 130,5 (n</sup>y^{= 13).}

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и делаем необходимые расчеты.
   

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2
117,0	-4,3	18,49	120,5	-5,6	31,36
118,5	-2,8	7,84	122,0	-4,1	16,81
120,0	-1,3	1,69	125,5	-0,6	0,36
122,0	0,7	0,49	126,0	-0,1	0,01
120,0	-1,3	1,69	123,5	-2,6	6,76
124,0	2,7	7,29	129,5	3,4	11,56
124,5	3,2	10,24	131,0	4,9	24,01
120,5	-0,8	0,64	124,0	-2,1	4,41
121,0	-0,3	0,09	126,0	-0,1	0,01
121,0	-0,3	0,09	125,0	-1,1	1,21
122,0	0,7	0,49	127,0	0,9	0,81
123,5	2,2	4,84	129,0	2,9	8,41
123,5	2,2	4,84	130,5	4,4	19,36
x̄ = 121,3		∑(xi — x̄)2= 58,72	y= 126,1		∑(yi — ȳ)2 = 125,08

2. 
   На основании расчета средних величин выборок выдвигаем рабочую гипотезу.
   

Рабочая гипотеза: т.к.x̄ = 121,3 с  ȳ = 126,1 с, то предположим, что исследу- емые группы Xпоказали более высокие результаты в беге на 800 м, чем группы Y.

3. 
   Подтвердим выдвинутое предположение расчетом величины t-критерия Стьюдента, используя формулу (2.2.4).
   

_{t =} ^|121,3 — 126,1^| ⋅ √13 ⋅ 13 ⋅ (13 + 13 — 2) ₌ 4,8 ⋅ √4056 _≈ 4,8 ⋅ 63,69 _{≈ 4,42.}

^ф √(58,72 + 125,08) ⋅ (13 + 13)

√^4778,8

69,13

Рассчитаем число степеней свободы по формуле (2.2.2):

^{k= n}x⁺ⁿy^{– 2 = 13 + 13 – 2 =24.}

5. 
   ^{Сравним расчетное значение t-критерия (t}ф ^{= 4,42) с табличным значением для k= 24 при}  ^{= 0,1% (} ^{= 99,9%) (прилож. 1) и сделать вывод.}
   

^{Вывод:т.к. t}ф^{= 4,42  t}st^{= 3,75 для k= 24 при  = 0,1%, то с уверенностью  =}

99,9% можно говорить о том, что различия результатов в беге на 800 м у двух групп исследуемых достоверны, т.е. в группе X данный показатель выше, чем в группе Y.

В спорте часто на одних и тех же спортсменах проводится измерение через некоторое время (до и после тренировочного занятия, до и после этапа тренировки и т.п.). При этом стараются определить, изменилось ли состоя- ние спортсменов. В таких случаях выборкивсегдаравночисленны(n_x=n_y), а все измерения могут быть объединены в пары (каждая пара – это резуль- таты измерений на одном человеке в начале и конце эксперимента). Подоб- ные выборки называют связанными (или коррелированными): между дан- ными первого и второго измерения может быть корреляция.

При сравнении двух малых групп с зависимыми вариантами методом Стьюдента расчет t-критерия проводится по формуле:

_{t =} ^|z̄|⋅√^n⋅(n–1)_{, (2.2.5)}

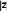
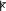
√^∑(z_i–z̄)²

где z_i=x_i–y_i;

  y; n– число испытуемых.

Расчет числа степеней свободы в данном случае, т. к. n_x=n_y, произво- дится по формуле:

k = 2  (n– 1). (2.2.6)

После того как произведен расчет t-критерия Стьюдента и числа сте- пеней свободы, из таблицы t-критерия Стьюдента (прилож. 1) находится критическое значение t-критерия для трех порогов доверительной вероят- ности  и уровней значимости . Если t_ф < t_st(минимального значения из таблицы), то между данными двух выборок не наблюдается достоверно- сти различий, то есть они примерно равные по данному показателю, и, следовательно, предложение о различиях в показателях выборок оказыва- ется ошибочным. Если же t_ф t_st, т. е. расчетная величина t-критерия со- ответствует табличным данным или выше их, то говорят о достоверности различий при определенной степени доверительной вероятности.