Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 9 из 37

Мода.

Мода(М_о)представляет собой значение признака, встречающееся в выборке наиболее часто.

Интервал группировки с наибольшей частотой называется модальным. Для определения моды используется следующая формула:


0 n
М = х + i ⋅ (^p1–p2), (2.1.5)

2p₁–p₂–p₃

где x_n– показатель нижней границы модального класса, т.е. класса с наибольшей частотой накопления вариант;

р₁– частота модального класса;

р₂– частота класса, предшествующего модальному;

р₃– частота класса, следующего за модальным;

i– интервал модального класса, который равен интервалу классов k.

Для данных результатов в беге на 30 м имеем:

0
M = 5,9 + 0,2 ⋅ ^{15 — 6}

30 —6 —4

= 5,9 + 0,2 ⋅ ⁹

20

= 5,99 ≈ 6,0 ^(с),

т.е. наибольшее число бегунов в исследуемой группе показали результат, близкий к 6,0 с.

На рисунке 2.1.1 представлена гистограмма распределения результа- тов в беге на 30 м с нанесенными на нее средним арифметическим, меди- аной и модой. Из приведенного графика видно, что указанные характер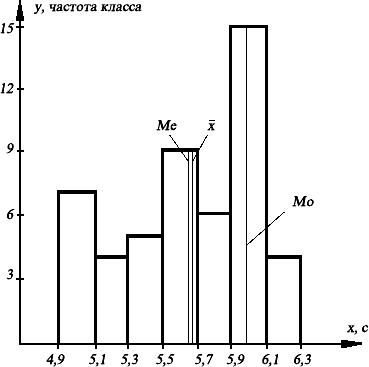и-

стики положения отличаются друг от друга. Это свидетельствует об асиммет- рии эмпирического распределения. Вообще, среднее, медиана и мода совпа- дают только в том случае, если распределение унимодальное (с одним мак- симумом) и симметричное. Чем больше распределение отличается от симмет- ричного, тем сильнее различие между этими характеристиками.

Рис. 2.1.1. Гистограмма распределения и характеристики положения результатов в беге на 30 м

Таким образом, расчет числовых значений характеристик положения поз- воляет выявить закономерность распределения показателей. При нормальном распределении данных необходимо соблюдение главного условия: полное совпадение по абсолютным величинам трех показателей: средней арифмети- ческой, медианы и моды. Если они имеют отличия, то распределение асим- метрично.

Характеристикирассеяния

Средние значения не дают полной информации о варьирующем при- знаке. Можно представить себе два эмпирических распределения, у кото- рых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляются и характеристики рассеяния выборки, такие как размах вариации, дисперсия, стандартноеотклонение, стандартная ошибка среднего арифметического и коэффи-циентвариации.