Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 6 из 37

Статистические методы обработки данных спортивно-педагогических исследований

Понятие о статистическом наблюдении, этапы его проведения. Прежде чем начать использование статистических методов спортивно-пе- дагогических исследований, нужно иметь в своем распоряжении исчер- пывающую информационную базу, в полной мере и достоверно описыва- ющую объект исследования. Процесс статистического исследования предполагает проведение таких этапов, как:

• 
  сбор информации по статистике (статистическое наблюдение) и ее первичная обработка;
  
• 
  группировка и последующая обработка данных, которые получены вследствие статистического наблюдения, на базе их сводки и группи- ровки;
  
• 
  обобщение и анализ результатов обработки статистических матери- алов, формулировка выводов и рекомендаций по результатам всего стати- стического исследования.
  

Следовательно, статистическое наблюдение – это первый и исходный этап статистического исследования.

Планомерность статистического наблюдения состоит в том, что оно проводится по специально разработанному плану, который содержит в себе вопросы, связанные с организацией и техникой сбора статистической информации, контроля ее достоверности и качества, представления ито- говых материалов.

Массовый характер статистического наблюдения обеспечивается наиболее полным диапазоном всех случаев проявления исследуемого яв- ления или процесса, т. е. количественные и качественные характеристики подвергаются измерению и регистрации не отдельных единиц изучаемой совокупности, а всей массы единиц совокупности в процессе статистиче- ского наблюдения.

Систематичность статистического наблюдения не должна носить сти- хийного характера. Работы, связанные с проведением такого наблюдения, должны выполняться либо непрерывно, либо регулярно, через одинако- вые интервалы времени.

Процесс подготовки статистического наблюдения предполагает уста- новление цели и объекта наблюдения, выбор единицы наблюдения, со- става признаков, подлежащих регистрации. Для сбора данных необхо- димо разработать бланки документов и выбрать средства и методы их по- лучения.

Следовательно, статистическое наблюдение является трудоемкой и кропотливой работой, которая требует привлечения квалифицированных кадров, всесторонне взвешенной ее организации, планирования, подго- товки и проведения.

Видыиспособыстатистическогонаблюдения.Статистическое наблюдение представляет собой процесс, который с точки зрения его ор- ганизации может иметь разнообразные способы, формы и виды проведе- ния. Задачей общей теории статистики является определение сущности

способов, форм и видов наблюдения для решения вопроса, где, когда и какие приемы наблюдения будут применяться.

Статистические наблюдения имеют две основные группы:

• 
  охват единиц совокупности;
  
• 
  время регистрации фактов.
  

По уровню охвата исследуемой совокупности статистическое наблю- дение делится на два типа: сплошное и несплошное.

Под сплошным(полным) наблюдением понимается охват всех единиц изучаемой совокупности. Сплошное наблюдение обеспечивает полноту информации об изучаемых явлениях и процессах. Для сбора и обработки всего объема необходимой информации требуется значительное время, поэтому потребность в оперативной информации не удовлетворяется. Не- редко сплошное наблюдение вообще невозможно (например, когда иссле- дуемая совокупность чересчур велика или отсутствует возможность по- лучения информации обо всех единицах совокупности). В результате этого проводят несплошные наблюдения.

Под несплошным наблюдением понимается только охват определен- ной части изучаемой совокупности. Проводя несплошное наблюдение, необходимо заблаговременно определить, какая именно часть исследуе- мой совокупности будет подвергнута наблюдению, и какой критерий бу- дет положен в основу выборки. Существует несколько видов несплош- ного наблюдения: выборочное; наблюдение основного массива; моногра- фическое.
Точность наблюдения и методы проверки достоверности данных. Каждое конкретное измерение величины данных, осуществляемое в процессе наблюдения, дает, как правило, приближенное значение вели- чины явления, в той или иной мере отличающееся от исходного значения

этой величины.

Точностью статистического наблюдения называется степень соот- ветствия какого-либо показателя или признака, исчисленного по матери- алам наблюдения, действительной его величине. Расхождение между ре- зультатом наблюдения и истинным значением величины наблюдаемого явления называется ошибкой наблюдения.

В зависимости от характера, стадии и причин возникновения разли- чают несколько типов ошибок наблюдения.

По своему характеру ошибки делятся на случайные и систематиче- ские. Случайные ошибки – это ошибки, возникновение которых обу- словлено действием случайных факторов. К ним относятся оговорки и описки опрашиваемого лица. Они могут быть направлены в сторону уменьшения или увеличения значения признака. На конечном результате они, как правило, не отражаются, так как взаимопогашаются при сводной обработке результатов наблюдения.

Систематические ошибки имеют одинаковую тенденцию либо к уменьшению, либо к увеличению значения показателя признака. Это свя- зано с тем, что измерения, например, производятся неисправным измери-

тельным прибором или ошибки являются следствием неясной формули- ровки вопроса программы наблюдения и др. Систематические ошибки представляют большую опасность, так как в значительной мере искажают результаты наблюдения.

В зависимости от стадии возникновения различают: ошибки регистра- ции; ошибки, возникающие в ходе подготовки данных к машинной обра- ботке; ошибки, проявляющиеся в процессе обработки на вычислительной технике.

К ошибкам регистрации относятся те неточности, которые возни- кают при записи данных в статистический формуляр (первичный доку- мент, бланк, отчет, переписной лист) или при вводе данных в вычисли- тельную технику, искажение данных при передаче через линии связи (те- лефон, электронную почту). Часто ошибки регистрации возникают из-за несоблюдения формы бланка, т. е. запись производится не в установлен- ную строку или графу документа. Случается и преднамеренное искажение значений отдельных показателей.

Ошибки при подготовке данных к машинной обработке или в процессе самой обработки возникают в вычислительных центрах или центрах под- готовки данных. Возникновение таких ошибок связано с небрежным, не- правильным, нечетким заполнением данных в формулярах, с физическим дефектом носителя данных, с потерей части данных вследствие несоблю- дения технологии хранения информационных баз. Иногда ошибки вы- званы сбоями в работе оборудования.

Зная виды и причины возникновения ошибок наблюдения, можно в значительной мере снизить процент подобных искажений информации. Различают несколько видов ошибок:

• 
  ошибки измерения, связанные с определенными погрешностями, ко- торые возникают при однократном статистическом наблюдении явления и процессов общественной жизни;
  
• 
  ошибки репрезентативности, возникающие в ходе несплошного наблюдения и связанные с тем, что сама выборка нерепрезентативна и ре- зультаты, полученные на ее основе, не могут распространяться на всю со- вокупность;
  
• 
  преднамеренные ошибки, возникающие по причине сознательного искажения данных с разными целями, среди которых желание приукра- сить действительное состояние объекта наблюдения или, наоборот, пока- зать неудовлетворительное состояние объекта и т. д. Следует заметить, что такое искажение информации является нарушением закона;
  
• 
  непреднамеренные ошибки, как правило, носящие случайный харак- тер и связанные с низкой квалификацией работников, их невнимательно- стью или небрежностью. Часто такие ошибки связаны с субъективными факторами, когда люди дают неправильную информацию о своем воз- расте, семейном положении, образовании, принадлежности к социальной группе и ином или просто забывают некоторые факты, сообщая регистра- тору информацию, которая только что возникла в памяти.
  

Статистические таблицы. После того как данные статистического наблюдения собраны и даже сгруппированы, их трудно воспринимать и

анализировать без определенной, наглядной систематизации. Результаты статистических сводок и группировок получают оформление в виде ста- тистических таблиц.

Статистическая таблица – таблица, которая дает количественную характеристику статистической совокупности и представляет собой форму наглядного изложения полученных в результате статистической сводки и группировки числовых (цифровых) данных. По внешнему виду она представляет собой комбинацию вертикальных и горизонтальных строк. В ней обязательно должны быть общие боковые и верхние заго- ловки. Еще одной особенностью статистической таблицы является нали- чие в ней подлежащего (характеристика статистической совокупности) и сказуемого (показателя, характеризующего совокупности). Статистиче- ские таблицы являются формой наиболее рационального изложения ре- зультатов сводки или группировки.

Подлежащеетаблицыпредставляет ту статистическую совокупность, о которой идет речь в таблице, т. е. перечень отдельных или всех единиц совокупности либо их групп. Чаще всего подлежащее помещается в левой части таблицы и содержит перечень строк.

Сказуемое таблицы – это те показатели, с помощью которых дается характеристика явления, отображаемого в таблице.

Подлежащее и сказуемое таблицы могут располагаться по-разному. Это технический вопрос, главное, чтобы таблица была легко читаемой, компактной и легко воспринималась.

В статистической практике и исследовательских работах использу- ются таблицы различной сложности. Это зависит от характера изучаемой совокупности, объема имеющейся информации, задач анализа. Если в подлежащем таблицы содержится простой перечень каких-либо объектов или территориальных единиц, таблица называется простой. В подлежащем простой таблицы нет каких-либо группировок статистических данных.

Простая таблица содержит только описательные сведения, ее аналити- ческие возможности ограничены. Глубокий анализ исследуемой совокуп- ности, взаимосвязей признаков предполагает построение более сложных таблиц – групповых и комбинационных.

Групповые таблицы в отличие от простых содержат в подлежащем не простой перечень единиц объекта наблюдения, а их группировку по од- ному существенному признаку. Простейшим видом групповой таблицы являются таблицы, в которых представлены ряды распределения. Группо- вая таблица может быть более сложной, если в сказуемом приводится не только число единиц в каждой группе, но и ряд других важных показате- лей, количественно и качественно характеризующих группы подлежа- щего. Такие таблицы часто используются в целях сопоставления обобща- ющих показателей по группам, что позволяет сделать определенные прак- тические выводы. Более широкими аналитическими возможностями рас- полагают комбинационные таблицы.

Комбинационными называются статистические таблицы, в подлежа- щем которых группы единиц, образованные по одному признаку, подраз- деляются на подгруппы по одному или нескольким признакам. В отличие

от простых и групповых таблиц комбинационные позволяют проследить зависимость показателей сказуемого от нескольких признаков, которые легли в основу комбинационной группировки в подлежащем.

Наряду с перечисленными выше таблицами в статистической прак- тике применяют таблицы сопряженности (или таблицы частот). В основе построения таких таблиц лежит группировка единиц совокупности по двум или более признакам, которые называются уровнями.

Перечислим основные правила построения статистических таблиц:

• 
  статистическая таблица должна быть компактной и отражать только те исходные данные, которые прямо отражают исследуемое социально- экономическое явление в статике и динамике;
  
• 
  заголовок статистической таблицы и название граф и строк должны быть четкими, краткими, лаконичными. В заголовке должны быть отра- жены объект, признак, время и место совершения события;
  
• 
  графы и строки следует нумеровать;
  
• 
  графы и строки должны содержать единицы измерения, для которых существуют общепринятые сокращения;
  
• 
  лучше всего располагать сопоставляемую в ходе анализа информа- цию в соседних графах (либо одну под другой). Это облегчает процесс ее сравнения;
  
• 
  для удобства чтения и работы числа в статистической таблице сле- дует проставлять в середине граф, строго одно под другим: единицы под единицами, запятая под запятой;
  
• 
  числа целесообразно округлять с одинаковой степенью точности (до целого знака, до десятой доли);
  
• 
  отсутствие данных обозначается знаком умножения «*», если данная позиция не подлежит заполнению, отсутствие сведений обозначается многоточием (...), либо н. д., либо н. св., при отсутствии явления ставится знак тире (-);
  
• 
  для отображения очень малых чисел используют обозначение 0.0
  

или 0.00;

• 
  если число получено на основании условных расчетов, то его берут в скобки, сомнительные числа сопровождают вопросительным знаком, а предварительные – знаком «!».
  

В случае необходимости дополнительной информации статистические таблицы сопровождаются сносками и примечаниями, в которых разъяс- няются, например, сущность специфического показателя, примененной методологии и т. д. Сносками пользуются для того, чтобы указать на огра- ничивающие обстоятельства, которые надо принять во внимание при чте- нии таблицы.

При соблюдении этих правил, статистическая таблица становятся ос- новным средством представления, обработки и обобщения статистиче- ской информации о состоянии и развитии изучаемых социально-экономи- ческих явлений.

Статистические группировки – первый этап статистической сводки, позволяющий выделить из массы исходного статистического материала

однородные группы единиц, обладающих общим сходством в качествен- ном и количественном отношениях. Важно понимать, что группировка – это не субъективный технический прием расчленения совокупности на части, а научно обоснованный процесс расчленения множества единиц совокупности по определенному признаку.

Самая простая группировка – ряд распределения. Рядами распределе-ния называются ряды чисел (цифр), характеризующие состав или струк- туру какого-либо явления после группировки статистических данных об этом явлении. Ряд распределения – это группировка, в которой для харак- теристики групп применяется один показатель – численность группы, т. е. это ряд чисел, показывающий, как распределяются единицы совокуп- ности по изучаемому признаку.

Ряды, построенные по атрибутивному признаку, называют атрибутив-ными рядами. Приведенный ряд распределения содержит три элемента: разновидности атрибутивного признака (мужчины, женщины); численно- сти единиц в каждой группе, называемые частотами ряда распределения; численности групп, выраженные в долях (процентах) от общей численно- сти единиц, называемые частостями.Сумма частостей равна 1, если они выражены в долях единицы, и 100%, если они выражены в процентах.

Ряды распределения, построенные по количественному признаку, называются вариационнымирядами. Числовые значения количественного признака в вариационном ряду распределения называются вариантами и располагаются в определенной последовательности. Варианты могут вы- ражаться числами положительными и отрицательными, абсолютными и относительными. Вариационные ряды делятся на:

• 
  дискретные;
  
• 
  интервальные.
  

Дискретные вариационные ряды характеризуют распределение еди- ниц совокупности по дискретному (прерывному) признаку, т. е. принима- ющему целые значения. При построении ряда распределения с дискрет- ной вариацией признака все варианты выписываются в порядке возраста- ния их величины, подсчитывается, сколько раз повторяется одна и та же величина варианта, т. е. частота, и записывается в одной строке с соответ- ствующим значением варианта. Частоты в дискретном вариационном ряду, как и в атрибутивном, могут быть заменены частостями.

В случае непрерывной вариации величина признака может принимать любые значения в определенном интервале, например распределение ра- ботников фирмы по уровню дохода.

При построении интервального вариационного ряда необходимо вы- брать оптимальное число групп (интервалов признака) и установить длину интервала. Оптимальное число групп выбирается так, чтобы отра- зить многообразие значений признака в совокупности. Чаще всего число групп устанавливается по формуле:

k = 1 + 3,32lgN = 1,441lgN + 1 (1.2.1)

где k – число групп;

N – численность совокупности.

Если полученная группировка не удовлетворяет требованиям анализа, то можно произвести перегруппировку. Не следует стремиться к очень большому количеству групп, так как в такой группировке нередко исче- зают различия между группами. Также надо избегать образования и слиш- ком малочисленных групп, включающих несколько единиц совокупно- сти, потому что в таких группах перестает действовать закон больших чи- сел и возможно проявление случайности. Когда не удается сразу наметить возможные группы, собранный материал сначала разбивают на значи- тельное количество групп, а затем укрупняют их, уменьшая количество групп и создавая качественно однородные группы.

Таким образом, во всех случаях группировки должны быть построены так, чтобы образованные в них группы как можно полнее отвечали действи- тельности, были бы видны различия между группами и не объединялись бы в одну группу существенно различающиеся между собой явления.

Распределением признака называется закономерность встречаемости разных его значений.

В спортивно-педагогических исследованиях чаще всего ссылаются на нормальное распределение. Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине – достаточно часто.

Нормальным такое распределение называется потому, что оно очень часто встречалось в естественнонаучных исследованиях и казалось «нор- мой» всякого массового случайного проявления признаков. Это распреде- ление следует закону, открытому тремя учеными в разное время: Муав- ром в 1733 г. в Англии, Гуассом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.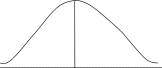





М

Рис. 1.2.1. График нормального распределения статистических данных

График нормального распределения представляет собой так называе- мую колоколообразную кривую.

Параметры распределения – это его числовые характеристики, указы- вающие, где «в среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака.

Наиболее практически важными параметрами являются математиче- ское ожидание, дисперсия, показатели асимметрии и эксцесса.

В реальных спортивно-педагогических исследованиях мы оперируем не параметрами, а их приближенными значениями, так называемыми оценками параметров. В дальнейшем, говоря о параметрах, мы будем иметь в виду их оценки.

Среднееарифметическое(оценка математического ожидания) вычис- ляется по формуле:

х̄ = М = ^∑хi, (1.2.2)

n

где х_i – каждое наблюдаемое значение признака;

i – индекс, указывающий на порядковый номер данного значения при- знака;

n – количество наблюдений;

 - знак суммирования.

Дисперсия

S² = ^{∑(xi–x̄)}2, (1.2.3)

n–1

где x_i – каждое наблюдаемое значение признака; x – среднее арифметическое значение признака; n – количество наблюдений.

Величина, представляющая собой квадратный корень из несмещенной оценки дисперсии (S), называется стандартным отклонением или сред-ним квадратическим отклонением. Обычно обозначают греческой бук- вой  (сигма)

_{σ = √}∑(x_i–x̄)²

n–1

(1.2.4)

В тех случаях, когда какие-нибудь причины благоприятствуют более частому появлению значений, которые выше или, наоборот, ниже сред- него, образуется асимметрические распределения.

При левосторонней или положительной асимметрии в распределении чаще всего встречаются более низкие значения признака, а при правосто- ронней или отрицательной более высокие.

Показатель асимметрии (А) вычисляется по формуле:


3
_{А =} ∑(х_i–x̄)³

n⋅σ

(1.2.5)

а) левая, положительная;


б) правая, отрицательная.

В тех случаях, когда какие-либо причины способствуют преимущест- венному появлению средних или близких к средним значений, образуется распределение с положительным эксцессом.

Если же в распределении преобладают крайние значения, причем од- новременно с более низкие, и более высокие, то такое распределение ха- рактеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двухвершинное.

Показатель эксцесса (Е) определяется по формуле:


4
_{Е =} ∑(x_i–x̄)⁴ _—3

n–σ

(1.2.6)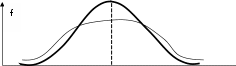


а) положительный эксцесс;


б) отрицательный эксцесс.

На практике исследователь может рассчитывать параметры любого распределения, если единицы, которые он использовал при измерении, признаются разумными в научном сообществе.

Статистические гипотезы. Формирование гипотез систематизирует предположения исследователя и представляет их в четком и лаконичном виде. Благодаря гипотезам исследователь не теряет путеводной нити в процессе расчетов и ему легко понять после их окончания, что, соб- ственно, он обнаружил.

Статистические гипотезы подразделяются на нулевые и альтернатив- ные, направленные и ненаправленные.

Нулевая гипотеза – это гипотеза об отсутствии различий. Она обозна- чается Н₀ называется нулевой потому, что содержит число 0: х₁ – х₂=0, где х₁, х₂ – сопоставляемые значения признаков.

Н₀ – это то, что мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий.

Альтернативная гипотеза – это гипотеза о значимости различий. Она обозначается Н₁. Н₁ – это то, что мы хотим доказать, поэтому иногда ее называют экспериментальной.

Бывают задачи, когда мы хотим доказать, как раз не значимость раз- личий, т.е. подтвердить нулевую гипотезу. Однако чаще нам все-таки тре- буется доказать значимость различий, т.к. они более информативны для нас в поиске нового.

Нулевая и альтернативная гипотеза могут быть направленными и не- направленными.

Если мы хотим доказать, что в группе А под влиянием каких-то экспе- риментальных воздействий произошли более выраженные изменения, чем в группе Б, то нам тоже необходимо сформулировать направленные гипотезы.

Если же мы хотим доказать, что различаются формы распределения признака в группе А и Б, то формируются ненаправленные гипотезы.

Статистические гипотезы

направленные ненаправленные нулевая альтернативная нулевая альтернативная

Проверка гипотез осуществляется с помощью критериев статистиче- ской оценки различий.

Статистические критерии. Статистический критерий – это решаю- щее правило, обеспечивающее надежное поведение, т.е. принятие истин- ной и отклонение ложной гипотезы с высокой вероятностью. Статистиче- ские критерии обозначают также метод расчета определенного числа и само это число.

Когда мы говорим, что достоверность различий определялась по кри- ^{терию t}^{, то имеет в виду что использовали метод Стьюдента для расчета определенного числа. Когда мы говорим, далее, что t}^{=2,6, то имеем в} виду определенное число, рассчитанное по методу Стьюдента. Это число обозначается как эмпирическое значение критерия.

По соотношению эмпирического и критического значений критерия можно судить о том, подтверждается ли или опровергается нулевая гипо- теза. Например, если t_эмп t_кр, Н₀ отвергается.

Критерии делятся на параметрические и непараметрические. Параметрическиекритерии – включающие в форму расчета параметры рас-

пределения, т.е. х, s (t – критерий Стьюдента, критерий F – Фишира и др.).

Непараметрические критерии – не включающие в форму расчета пара- метров распределения и основанные на оперировании частотами или ран- гами критерий Т – Вилкоксона, критерий W – Манна-Уитни и др.).

И те, и другие критерии имеют свои преимущества и недостатки.

Из всего мы видим, что параметрические критерии могут оказаться не- сколько более мощными, чем не параметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен.

По сравнению с параметрическими критериями они ограничены лишь в одном – с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака. Эту за- дачу может решить только дисперсионный двухфакторный анализ

Таблица 1.2.1

Статистические критерии

Параметрические критерии	Непараметрические критерии
1. Позволяют прямо оценить различия в средних, получен- ных в двух выборках (t-крите- рий Стьюдента)	1. Позволяют оценить лишь средние тенден- ции, например. Ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б – более низкие значения признака (критерии Q, U, W, * и др.)
2. Позволяют прямо оценить различия в дисперсиях (крите- рий Фишера)	2. Позволяют оценить лишь различия в диапа- зонах вариативности признака (критерий *)
3. Позволяют выявить тенден- ции измерения признака при переходе от условия к условию (дисперсионный и однофактор- ный анализ), но лишь при усло- вии нормального распределе- ния признака	3. Позволяют выявить тенденции изменения признака при переходе от условия к усло- вию при любом распределении признака (критерии тенденции L и S)

Окончаниетаблицы1.2.1

Параметрические критерии	Непараметрические критерии
4. Позволяют оценить взаимо- действие двух или более факто- ров и их влиянии на изменения признака (двух факторный дис- персионный анализ)	4. Эта возможность отсутствует
5. Экспериментальные данные должны отвечать двум, а ино- гда трем условиям: значения признака измерены по интервальной шкале; распределение признака яв- ляется нормальным; в дисперсионном анализе должно соблюдаться требова- ние равенства дисперсий в ячейках комплекса	5. Экспериментальные данные могут не от- вечать ни одному из этих условий: значения признака могут быть представ- лены в любой шкале, начиная от шкалы наименований; распределение признака может быть лю- бым и совпадение с каким-либо теоретиче- ским законом распределения – необяза- тельно и не нуждается в проверке; требование равенства дисперсий отсут- ствует
6. Математические расчеты до- вольно сложны	6. Математические расчеты по большей ча- сти просты и занимают мало времени (за ис- ключением критериев 2 )
7. Если условия, перечислен- ные в п.5, выполняются, пара- метрические критерии оказыва- ются несколько более мощ- ными, чем непараметрические	7. Если условия, перечисленные в п. 5, не выполняются, непараметрические критерии оказываются более мощными, чем парамет- рические, т.к. они менее чувствительны к «засорением»

Уровеньстатистическойдостоверности.Мощностькритериев.Уровень значимости – это вероятность того, что мы сочли различия суще- ственными, а они на самом деле случайны.

Если:

=95%, то =5%	0,95	0,05
=99%, то =1%	0,99	0,01
=99,9%, то =0,1%	0,999	0,001

Уровеньзначимости– это вероятность отклонения нулевой гипотезы, в то время как она верна.

Ошибка, состоящая в том, что мы отклонили нулевую гипотезу, в то время как она верна, называется ошибкой1рода.

Вероятность такой ошибки обычно обозначается  (обозначается не

0,05 или 0,01, а 0,05, 0,01).

Если вероятность ошибки – это , то вероятность правильного реше- ния: 1-. Чем меньше ,тем больше вероятность правильного решения.

Принято считать низшим уровнем статистической значимости 5%- ный уровень (0,05); достаточным – 1%-ный уровень (0,01) и высшим 0,1%-ный уровень (0,001).

Мощность критерия – это его способность выявлять различия, если они есть. Т.е. это его способность отклонить нулевую гипотезу об отсут- ствии различий, если она неверна.

Ошибка, состоящая в том, что мы приняли нулевую гипотезу, в то время как она неверна, называется ошибкой2рода.

Вероятность такой ошибки обозначается как .

Мощность критерия – это его способность не допускать ошибку 2

рода. Поэтому Мощность = 1 – .

Мощность критерия определяется эмпирическим путем. Одни и те же задачи могут быть решены с помощью разных критериев, при этом обна- руживается, что некоторые критерии позволяют выявить различия там, где другие оказываются неспособными это сделать, или выявляют более высокий уровень значимости различий.

Возникает вопрос: а зачем же тогда использовать менее мощные кри- терии? Да, дело в то, что основанием для выбора критерия может быть не только мощность, но и другие характеристики:

• 
  простота;
  
• 
  более широкий диапазон использования;
  
• 
  применимость по отношению к неравным по объему выборкам;
  
• 
  большая информативность результатов.