|
|
карточки. Назначение тематических контрольных работ
Максимальный балл за выполнение всей работы – 9баллов. Критерии оценивания.
№ задания
|
Количество баллов
|
|
0 баллов – неправильный ответ
|
1
|
Максимальное количество баллов 1
|
2
|
Максимальное количество баллов 1
|
3
|
Максимальное количество баллов 1
|
4
|
Максимальное количество баллов 1
|
5
|
Максимальное количество баллов 1
|
6
|
Максимальное количество баллов 1
|
7
|
Максимальное количество баллов 1
|
8
|
Максимальное количество баллов 2
|
итого
|
9 баллов
|
За выполнение контрольной работы учащиеся получают школьные отметки по пятибалльной шкале.
Пересчёт первичного балла
за выполнение входной контрольной работы в отметку по пятибалльной шкале
Баллы
|
Отметка
|
9 баллов
|
Отметка «5»
|
7-8 баллов
|
Отметка «4»
|
5-6 баллов
|
Отметка «3»
|
0-4 баллов
|
Отметка «2»
|
не приступил к выполнению заданий
|
Отметка «1»
|
Обобщенный план варианта контрольных измерительных материалов
для проведения контрольной работы по математике в 11 классах в декабре 2018 г.
Демонстрационный вариант.
1.Найдите производную функции 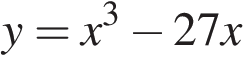 . .
2.На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
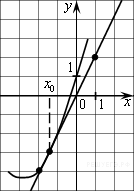
3.Материальная точка движется прямолинейно по закону 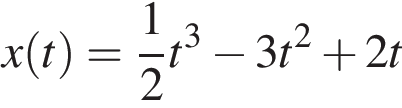 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с. (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
4.В цилиндрическом сосуде уровень жидкости достигает 36 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 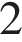 раза больше первого? Ответ выразите в см. раза больше первого? Ответ выразите в см.
5.Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
6.Найдите точку максимума функции 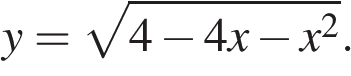
Найдите производную функции 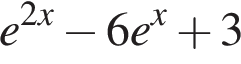
а) Решите уравнение 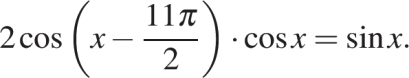
б) Найдите все корни этого уравнения, принадлежащие отрезку 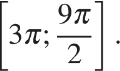
|
№
задания
|
Уровень сложности
|
Максима льный
балл
|
КЭС
|
Предметные результаты
|
1
|
Базовый
|
1
|
4.1.1
|
Понятие о производной функции, геометрический
смысл производной
|
2
|
Базовый
|
1
|
4.1.1
|
Понятие о производной функции, геометрический
смысл производной
|
3
|
Базовый
|
1
|
4.1.2,
4.1.3
|
Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком.
Уравнение касательной к графику функции. Цилиндр
|
4
|
Базовый
|
1
|
5.4.1
|
. Основание, высота, боковая поверхность,
образующая, развертка
|
5
|
Базовый
|
1
|
5.4.2
|
Конус. Основание, высота, боковая поверхность, образующая, развертка
|
6
|
Базовый
|
1
|
4.1.5,
4.2.1
|
Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков
|
7
|
Базовый
|
1
|
4.1.5,
4 1.4,
4.21
|
Производные суммы, разности, произведения, частного, Производные основных элементарных функций, Применение производной к исследованию функций и
построению графиков
|
8
|
Повышенный
|
2
|
2.1.4
|
Тригонометрические уравнения
|
  Ответы к демонстрационному варианту Ответы к демонстрационному варианту
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
3х2-27
|
0,5
|
20
|
9
|
3
|
-2
|
2е2х-6е
|
а)Пn; -2/3 Пn; 2/3 Пn, n из Z в) 8/3 П, 10/3 П, 3П, 4П.
|
Вариант-1.
1.Найдите производную функции 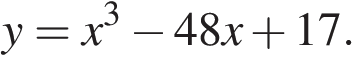
2.На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0.
Найдите значение производной функции f(x) в точке x0.
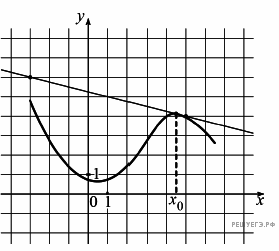
3.Материальная точка движется прямолинейно по закону 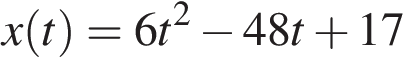 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с. (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
4.В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 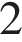 раза больше первого? Ответ выразите в см. раза больше первого? Ответ выразите в см.

5.Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?

 Найдите точку минимума функции Найдите точку минимума функции
Найдите производную функции
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие промежутку 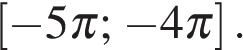
Вариант-2.
1.Найдите производную функции 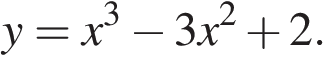
2.На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0.
Найдите значение производной функции f(x) в точке x0.
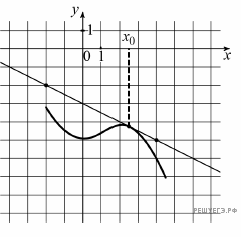
3.Материальная точка движется прямолинейно по закону  (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени 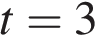 с. с.
4.В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12
см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.

 5.Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 2,5 раза, а высота останется прежней? 5.Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 2,5 раза, а высота останется прежней?
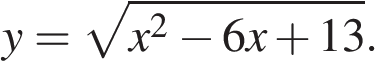 6.Найдите наименьшее значение функции 6.Найдите наименьшее значение функции
 Найдите производную функции Найдите производную функции
а) Решите уравнение
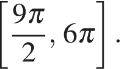 б) Найдите все корни этого уравнения, принадлежащие отрезку б) Найдите все корни этого уравнения, принадлежащие отрезку
|
|
|
 Скачать 3.72 Mb.
Скачать 3.72 Mb.
 Ответы к демонстрационному варианту
Ответы к демонстрационному варианту

 Найдите точку минимума функции
Найдите точку минимума функции

 5.Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 2,5 раза, а высота останется прежней?
5.Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 2,5 раза, а высота останется прежней? Найдите производную функции
Найдите производную функции
