ПОДГОТОВКА К ЕГЭ (с ответами). Название планеты

• Название: Название планеты
• Дата: 12.04.2022
• Размер: 0.52 Mb.
• Имя файла: ПОДГОТОВКА К ЕГЭ (с ответами).docx
• Тип: Документы; #467094
• страница: 8 из 8

Ответ: 0,21 м.


Задание 76. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 36 см, запертый столбиком ртути длиной l = 15 см. Определите длину l2 воздушного столбика под ртутью, если трубку поставить вертикально отверстием вверх. Атмосферное давление 750 мм рт. ст. Температуру воздуха в трубке считать постоянной.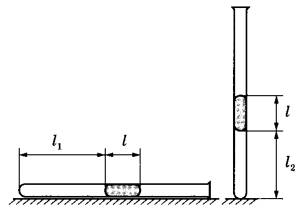



Решение.

1. Когда трубка расположена горизонтально, объём воздуха и его давление равны, соответственно:  , где S — площадь сечения трубки;  , что вытекает из условия равновесия столбика ртути.

2. Когда трубка расположена вертикально отверстием вверх, объём закрытой части трубки и давление воздуха в ней равны, соответственно:

,

где ρ — плотность ртути.

3. Так как T = const, получаем:  .  , откуда

 см.

Ответ: 30 см.


Задание 77. В тепловом двигателе 2 моль аргона совершают цикл 1-2-3-4-1, показанный на графике в координатах р-Т, где p — давление газа, T — абсолютная температура. Температуры в точках 2 и 4 равны, а температура в точке 3 в 4 раза больше температуры в точке 1. Определите КПД цикла.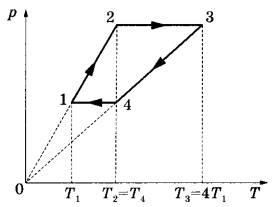



Решение.

1. Коэффициент полезного действия теплового двигателя определяется формулой  , где A – работа, совершённая газом за цикл, Q1 — количество теплоты, полученное за цикл газом от нагревателя.

2. Анализируя график цикла, можно прийти к выводу, что цикл состоит из двух изохор, 1 -2 и 3—4, и двух изобар, 2-3 и 4-1 (см. рисунок цикла в координатах p-V).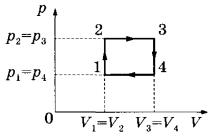



Согласно закону Шарля для двух изохор 1-2 и 3-4   и  . Следовательно,  . Так как  , то   и  .

3. Согласно закону Гей-Люссака  ; так как  , то  . Работа, совершённая газом за цикл, численно равна площади фигуры, ограниченной графиком цикла:  .

Газ получает положительное количество теплоты на изохоре 1-2 и изобаре 2-3: таким образом,  .

4. Согласно первому закону термодинамики для изохорного процесса 1-2 (V = const: А = 0)

.

Для изобарного процесса 2-3:

.

С учётом уравнения Менделеева-Клапейрона, pV = RT, получаем:



Таким образом,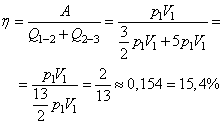



Ответ: 15,4%.


Задание 78. На горизонтальном столе лежат два параллельных друг другу рельса: a и b, замкнутых двумя одинаковыми металлическими проводниками: АС и ED (см. рисунок). Вся система проводников находится в однородном магнитном поле, направленном вертикально вниз. Модуль индукции магнитного поля равен Б, расстояние между рельсами скорости проводников v1 и v2 сопротивление каждого из проводников R. Какова сила тока в цепи? Сопротивлением рельсов пренебречь.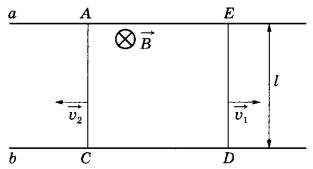



Решение.

1. Согласно закону электромагнитной индукции ЭДС в контуре AEDC пропорциональна скорости изменения потока вектора магнитной индукции:

.

2. По закону Ома для полной цепи сила тока в этом контуре

.

3. Объединяя формулы, получим:

.

Ответ:  .


Задание 79. По горизонтально расположенным проводящим шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 50 г и сопротивлением R каждый. Расстояние между рельсами 1 = 20 см, а коэффициент трения между стержнями и рельсами μ = 0,2. Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией В = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Скорость движения первого стержня относительно второго   = 1,5 м/с. Определите R. Самоиндукцией контура пренебречь.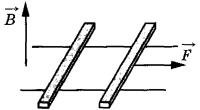



Решение.

При движении стержней с разными скоростями изменение потока вектора магнитной индукции, пронизывающего контур, за промежуток времени ∆t определяется по формуле

,

что приводит к возникновению в контуре ЭДС индукции. Согласно закону Фарадея  .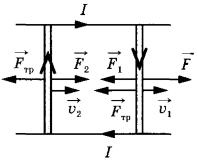



Здесь мы пренебрегли самоиндукцией контура. В соответствии с законом Ома для замкнутой цепи в контуре появился ток

На проводники с током в магнитном поле действуют силы Ампера F1 и F2.  , как показано на рисунке. Кроме этих сил, на каждый стержень действует тормозящая сила трения,  .

Так как стержни движутся равномерно, сумма сил, приложенных к каждому стержню, равна нулю. На второй стержень действуют только сила Ампера F2, и сила трения, поэтому  . Отсюда сопротивление проводников: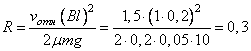

 Ом.

Ответ: 0,3 Ом.


Задание 80. На рисунке показана схема устройства для предварительного отбора заряженных частиц из источника частиц (и.ч.) для последующего детального исследования. Устройство представляет собой конденсатор, пластины которого изогнуты дугой радиусом R. Предположим, что в промежутке между обкладками конденсатора, не касаясь их, пролетают молекулы интересующего нас вещества, потерявшие один электрон. Во сколько раз нужно изменить напряжение на обкладках конденсатора, чтобы сквозь него могли пролетать такие же ионы, но имеющие в 2 раза большую кинетическую энергию? Считать, что расстояние между обкладками конденсатора мало, напряжённость электрического поля в конденсаторе всюду одинакова по модулю, а вне конденсатора электрическое поле отсутствует. Влиянием силы тяжести пренебречь.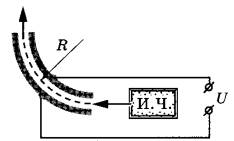



Решение.

Центростремительное ускорение иона в конденсаторе   определяется силой Кулона F = qE, действующей со стороны электрического поля. По второму закону Ньютона  , где q, m и v — соответственно заряд, масса и скорость иона, Е — напряженность электрического поля. С другой стороны, кинетическая энергия тела определяется соотношением  . Отсюда:  . Если   увеличивается в 2 раза, то для сохранения прежнего значения радиуса траектории иона напряженность поля нужно тоже увеличить в 2 раза. Поскольку напряжённость электрического поля E прямо пропорциональна напряжению между обкладками конденсатора U, следовательно, его нужно увеличить в 2 раза.

Ответ: увеличить в 2 раза.


Задание 81. Вольт-амперная характеристика лампы накаливания изображена на графике. Если на лампу подать напряжение 12 В, то температура нити лампы равна 3500 К. Сопротивление нити прямо пропорционально её температуре. При какой температуре накала нити потребляемая лампой мощность составит 8,4 Вт?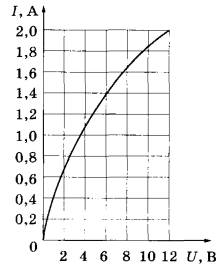



Решение.

1. Потребляемая лампой мощность пропорциональна напряжению на ней и силе тока через нить накала в соответствии с законом Джоуля-Ленца: Р = I∙U.

2. Как следует из графика, при напряжении   В сила тока, протекающего через лампу,   А.

3. Сопротивление лампы при этих параметрах определяется законом Ома для

участка цепи:

 Ом.

4. Как следует из графика, лампа потребляет мощность Р=8,4 Вт при напряжении U2 =6 В и силе тока I2 = 1,4 А, а сопротивление нити накала при этом напряжении

 Ом.

5. Так как сопротивление нити пропорционально температуре:  , то

,

откуда

 К.

Ответ: 2500 К.

Задание 82. В цепи, изображённой на рисунке, сопротивление диода в прямом направлении пренебрежимо мало, а в обратном многократно превышает сопротивление резисторов. При подключении к точке А положительного полюса, а к точке В отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым внутренним сопротивлением потребляемая мощность равна 14,4 Вт. При изменении полярности подключения батареи потребляемая мощность оказалась равной 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи.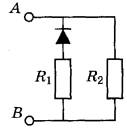



Решение.

1. Если при подключении батареи потенциал точки A оказывается выше, чем потенциал точки B,  , то ток через диод не течёт, и эквивалентная схема цепи имеет вид, изображённый на рис. 1. Потребляемая мощность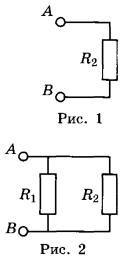

.



2. При изменении полярности подключения батареи  , диод открывается и подключает резистор R1 параллельно резистору R2. Эквивалентная схема цепи в этом случае изображена на рис. 2. При этом потребляемая мощность увеличивается:

.

3. Из этих уравнений:

.

4. Подставляя значения физических величин, указанные в условии, получаем: R1 = 20 Ом, R2 = 10 Ом.

Ответ: R1 = 20 Ом, R2 = 10 Ом.


Задание 83. На плоскую алюминиевую пластинку падает электромагнитное излучение. Фотоэлектроны удаляются от поверхности пластинки на расстояние не более 2 см в задерживающем однородном электрическом поле, перпендикулярном пластинке. Напряжённость поля 120 В/м. Работа выхода электрона с поверхности цинка 4,2 эВ. Какова длина волны падающего излучения?

Решение.

1. Максимальная кинетическая энергия фотоэлектронов, вылетающих из пластины, Wmax определяется уравнением Эйнштейна для фотоэффекта:

.       (1)

2. Максимальное удаление от пластины d для электрона с зарядом e в электрическом поле E определяется законом сохранения энергии:

.           (2)

3. Отсюда:  .

4. Подставляя значения физических величин, получим:

 нм.

Ответ: 188 нм.


Задание 84. Колебательный контур радиоприёмника настроен на длину волны λ = 2000 м. Индуктивность катушки контура L = 6 мкГн, максимальный ток в ней Imax = 1,6 мА. В контуре используется плоский воздушный конденсатор, расстояние между пластинами которого d = 2 мм. Чему равно максимальное значение напряжённости электрического поля в конденсаторе в процессе колебаний?

Решение.

Согласно закону сохранения энергии

       (1)

 (C – ёмкость конденсатора, Umax — максимальное напряжение на конденсаторе). Формула Томсона для периода электромагнитных колебаний в контуре:

.           (2)

Формула, связывающая длину волны с периодом колебаний:

(c – скорость света). Решив систему уравнений (1)-(3), находим величину Umax, откуда получаем для искомой напряжённости поля конденсатора: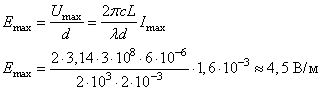



Ответ: 4,5 В/м.