ПОДГОТОВКА К ЕГЭ (с ответами). Название планеты

• Название: Название планеты
• Дата: 12.04.2022
• Размер: 0.52 Mb.
• Имя файла: ПОДГОТОВКА К ЕГЭ (с ответами).docx
• Тип: Документы; #467094
• страница: 7 из 8

Решение.

Согласно первому закону термодинамики

,

где A – совершенная газом работа; ∆U – изменение внутренней энергии газа; Q – количество теплоты, сообщенное газу. Работа газа  , и, записывая уравнение Менделеева-Клапейрона, имеем:

.

Изменение внутренней энергии для аргона (j=3 для идеального газа), можно записать в виде

,

следовательно, количество теплоты Q, равно:

 кДж.

Ответ: 15.


Задание 60. На рисунке изображён процесс, происходящий с 1 моль гелия. Минимальное давление газа p1 = 100 кПа, минимальный объём V1 = 10 л, а максимальный V2 = 30 л. Какую работу совершает гелий при переходе из состояния 1 в состояние 2?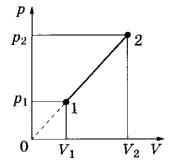



Решение.

Работа, совершенная газом, равна площади под графиком pV-диаграммы. Так как имеется линейная зависимость между p и V, исходящая из нулевой точки, то  , откуда   (здесь кПа переведены в Па, а литры в куб. м). Тогда, значение   кПа. И площадь под графиком pV-диаграммы (площадь трапеции), равна: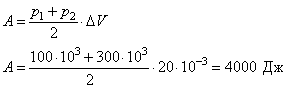



что составляет 4 кДж.

Ответ: 4.


Задание 61. Электрическая цепь состоит из аккумулятора с ЭДС 9 В и внутренним сопротивлением 2 Ом, лампочки, ключа и соединительных проводов. Какова сила тока в цепи, если напряжение на аккумуляторе равно 7,5 В? Сопротивлением проводов пренебречь.

Решение.

Так как напряжение на аккумуляторе 7,5 В соответствует падению напряжения во внешней цепи, то есть на лампочке, следовательно, падение напряжения на самом аккумуляторе, равно:

 В.

Учитывая, что внутреннее сопротивление аккумулятора r = 2 Ом, сила тока в цепи

 А.

Ответ: 0,75.


Задание 62. По параллельным проводникам bc и ad, находящимся в магнитном поле с индукцией B = 0,4 Тл, скользит проводящий стержень MN, который находится в контакте с проводниками (см. рисунок). Расстояние между проводниками l = 20 см. Слева проводники замкнуты резистором с сопротивлением R = 2 Ом. Сопротивление стержня и проводников пренебрежимо мало. При движении стержня через резистор R протекает ток I = 40 мА. С какой скоростью движется проводник? Считать, что вектор B перпендикулярен плоскости рисунка.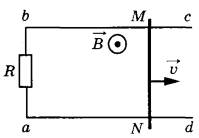



Решение.

При движении стержня в контуре возникает ЭДС  , где изменение магнитного потока  , и таким образом  . ЭДС вызывает появление тока  . Из полученного соотношения получаем:

 м/с.

Ответ: 1.


Задание 63. Действительное изображение предмета, полученное с помощью тонкой собирающей линзы, находится на расстоянии 12 см от линзы. Оптическая сила линзы 15 дптр. Определите расстояние от линзы до предмета.

Решение.

Оптическая сила линзы D связана с фокусным расстоянием F выражением:  . Запишем уравнение для тонкой собирающей линзы при условии действительного изображения:

,

где d – расстояние от предмета до линзы; f = 0,12 м – расстояние от линзы до изображения предмета. Найдем расстояние d от линзы до предмета: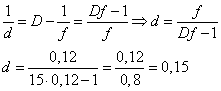



что составляет 15 см.

Ответ: 15.


Задание 64. На дифракционную решётку, имеющую 500 штрихов на 1 мм, перпендикулярно её поверхности падает узкий луч монохроматического света частотой   Гц. Каков максимальный порядок дифракционного максимума, доступного для наблюдения?

Решение.

Найдем период дифракционной решетки, который определяет число штрихов на 1 мм, имеем:  . Формула дифракционной решетки имеет вид:

,

где n - целое число;   - угол между решеткой и распространением света;   метров, что составляет   мм – длина волны. Порядок дифракционного максимума можно найти как

Ответ: 3.

• 
  
  

Задание 65. В двух идеальных колебательных контурах с одинаковой индуктивностью происходят свободные электромагнитные колебания, причём период колебаний в первом контуре   с, во втором   с. Во сколько раз амплитудное значение силы тока во втором контуре больше, чем в первом, если максимальный заряд конденсаторов в обоих случаях одинаков?

Решение.

Амплитудное значение силы тока в контуре связана с периодом колебаний и максимальным значением заряда конденсатора соотношением

.

Так как заряды в обоих случаях одинаковы, то отношение максимальных значений токов, дает:

,

то есть в 3 раза.

Ответ: 3.


Задание 66. В тонкой рассеивающей линзе получено уменьшенное в 4 раза изображение предмета. Определите модуль фокусного расстояния линзы, если изображение предмета находится на расстоянии f = 9 см от линзы.

Решение.

Запишем формулу тонкой рассеивающей линзы, имеем:

,

где f – расстояние между изображением предмета и линзой; d – расстояние между предметом и линзой; F – фокусное расстояние линзы. По условию задания сказано, что изображение предмета в 4 раза меньше, то есть можно записать, что  , откуда   (см. подобные треугольники на рисунке ниже).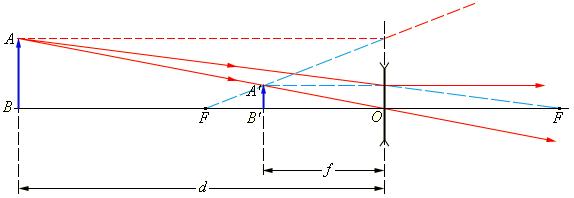



Тогда формула для тонкой линзы перепишется в виде:

или

 см.

Ответ: 12.


Задание 67. В двух идеальных колебательных контурах с одинаковыми конденсаторами происходят свободные электромагнитные колебания, причём период колебаний в первом контуре   с, во втором   с. Во сколько раз амплитудное значение напряжения на конденсаторе во втором контуре меньше, чем в первом, если максимальная сила тока в обоих случаях одинакова?

Решение.

Амплитудное значение силы тока в контуре связана с периодом колебаний и максимальным значением заряда конденсатора соотношением

.

Так как максимальная сила тока в обоих случаях одинакова, то отношение максимальных зарядов, дает:

и, так как,   (емкости C равны, т.к. конденсаторы одинаковы), получаем:

,

то есть в 4 раза.

Ответ: 4.


Задание 68. Максимальная кинетическая энергия электронов, вылетающих из металла под действием света, равна 1,2 эВ. Если увеличить частоту падающего света в 2 раза, то максимальная кинетическая энергия электронов, вылетающих из этого же металла, станет равной 3,95 эВ. Определите работу выхода электронов с поверхности металла.

Решение.

1. Запишем формулу Эйнштейна для фотоэффекта в первом случае:

,

где   - кинетическая энергия электронов; A – работа выхода. Если частоту волны v1 увеличить в 2 раза, то есть взять  , то учитывая, независимость работы выхода A от частоты падающего света, имеем:

Следовательно, работа выхода, равна: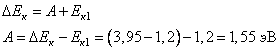



Ответ: 1,55.


Задание 69. На столе установили два незаряженных электрометра и соединили их медным стержнем с изолирующей ручкой (рис. 1). Затем к первому электрометру поднесли, не касаясь шара, отрицательно заряжённую палочку (рис. 2). Не убирая палочки, убрали стержень, а затем убрали палочку.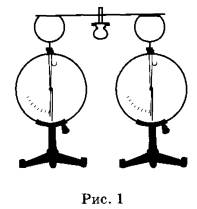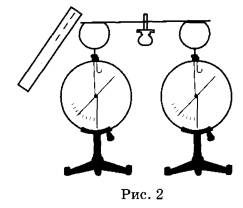

 

Ссылаясь на известные Вам законы и явления, объясните, почему электрометры оказались заряженными, и определите знаки заряда каждого из электрометров после того, как палочку убрали.

Решение.

1. Электрометр 1 имеет положительный заряд, а электрометр 2 — отрицательный.

2. Отрицательно заряженная палочка, поднесённая к шару электрометра 1, создаёт электрическое поле. В этом поле электроны с шара, стержня и стрелки электрометра 1 перемещаются по медному стержню на электрометр 2.

3. Поскольку два соединённых медным стержнем электрометра образуют изолированную систему, то согласно закону сохранения заряда положительный заряд электрометра 1 в точности равен по модулю отрицательному заряду электрометра 2.

4. После того как убрали стержень, показания электрометров не изменились.


Задание 70. На графике представлена зависимость давления неизменной массы идеального газа от его плотности. Опишите, как изменяются в зависимости от плотности температура и объём газа в процессах 1-2 и 2-3.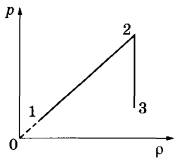



Решение.

1. Плотность газа  , где m — масса газа, V — его объём. В соответствии

с уравнением Менделеева-Клапейрона  . На участке 1-2 давление изменяется пропорционально плотности газа:  . Следовательно, в этом процессе температура газа не изменяется. Поскольку плотность газа на этом участке возрастает, объём газа уменьшается.

2. В процессе 23 плотность газа постоянна, следовательно, объём газа не меняется. Давление газа при этом уменьшается, следовательно, согласно уравнению Менделеева-Клапейрона температура газа также уменьшается.


Задание 71. В камере, из которой откачан воздух, создали электрическое поле напряжённостью E и магнитное поле с индукцией B. Поля однородные,  . В камеру влетает протон p, вектор скорости которого перпендикулярен Е и В как показано на рисунке. Модули напряжённости электрического поля и индукции магнитного поля таковы, что протон движется прямолинейно. Объясните, как изменится начальный участок траектории протона, если напряжённость электрического поля уменьшить. В ответе укажите, какие явления и закономерности Вы использовали для объяснения. Влиянием силы тяжести пренебречь.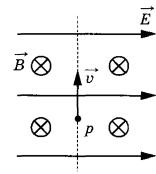



Решение.

1. Траектория протона будет криволинейной, отклоняющейся от пунктирной прямой влево.

2. На протон действуют магнитное поле силой  и электрическое поле силой  . Поскольку заряд протона положительный,   сонаправлена с E, а по правилу левой руки   направлена противоположно силе  . Поскольку первоначально протон двигался прямолинейно, то согласно третьему закону Ньютона по модулю эти силы были равны.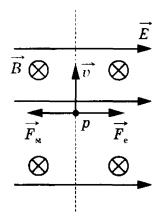



3. Сила действия электрического поля с уменьшением напряжённости электрического поля уменьшится. Поскольку из-за этого равнодействующая сил   и  , а также вызываемое ею в этом случае ускорение направлены влево, траектория протона будет криволинейной, отклоняющейся от пунктирной прямой влево.


Задание 72. От груза, неподвижно висящего на невесомой пружине жёсткостью k = 400 Н/м, отделился с начальной скоростью, равной нулю, его фрагмент. После этого при возникших колебаниях оставшаяся часть груза поднималась на максимальную высоту h = 3 см относительно первоначального положения. Какова масса m отделившегося от груза фрагмента?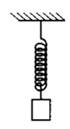



Решение.

1. На систему тел «груз + пружина» действует внешняя сила — сила тяжести, работа которой определяет изменение потенциальной энергии груза в поле силы тяжести. Силы трения в системе отсутствуют, следовательно, их работа равна нулю, и полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Нулевое значение потенциальной энергии в поле тяжести выбираем в начальном состоянии системы, нулевое значение потенциальной энергии деформации пружины — в положении нерастянутой пружины.



2. В начальном состоянии и на максимальной высоте кинетическая энергия системы «пружина + оставшаяся часть груза» равна нулю. Тогда в соответствии с законом сохранения механической энергии

,

где М — масса оставшейся части груза,   — длина пружины в нерастянутом состоянии,   — длина пружины в исходном состоянии,   — длина пружины в состоянии максимального подъёма оставшейся части груза.

3. В исходном состоянии груз находится в равновесии:

.

4. Из 2) и 3) с учётом того, что   и  , получим:

 кг.

Ответ: 0,6 кг.


Задание 73. Свинцовый шар массой 4 кг подвешен на нити и полностью погружён в воду (см. рисунок). Нить образует с вертикалью угол α = 30°. Определите силу, с которой нить действует на шар. Плотность свинца ρ = 11 300 кг/м3. Трением шара о стенку пренебречь. Сделайте схематический рисунок с указанием сил, действующих на шар.



Решение.

Систему отсчёта, связанную с Землёй, считаем инерциальной. Запишем второй закон Ньютона:

.



Поскольку трение шара о стенку отсутствует, линия действия силы натяжения нити будет проходить через центр шара. В проекциях на оси Ох и Оу второй закон Ньютона запишем в виде:

           (1)

  (2)

Объём шара  . Величина выталкивающей силы   определяется по закону Архимеда:

,                   (3)

где   — плотность воды. Выполняя математические преобразования с формулами (2) и (3), получим:

 Н.

Ответ: 42 Н.


Задание 74. Небольшой кубик массой m = 1,5 кг начинает скользить с высоты Н = 2,45 м с нулевой начальной скоростью по гладкой горке, переходящей в «мёртвую петлю» радиусом R = 1,5 м (см. рисунок). На какой высоте h от нижней точки петли сила давления кубика на стенку петли F = 4 Н? Сделайте рисунок с указанием сил, поясняющий решение.



Решение.

1. Пусть скорость кубика на высоте h равна v, а в нижней точке петли потенциальная энергия кубика равна нулю. Тогда по закону сохранения механической энергии

.



2. Когда кубик находится на высоте h, на него действуют две силы: сила тяжести mg и сила реакции опоры N. Запишем второй закон Ньютона в проекциях на радиальное направление (Ох на рисунке):

,

где   — центростремительное ускорение кубика в этой точке.

По третьему закону Ньютона N = F. Из рисунка видно, что  .

3. Из выражений п. 2 получим скорость кубика на высоте h:

.

4. Подставив полученное значение   в формулу п. 1, найдём искомую высоту:



Ответ: 2 м.


Задание 75. На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 100 г и m2 = 400 г, связанные нерастяжимой невесомой нитью длиной l. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). При вращении штанги с частотой 900 об/мин модуль силы натяжения нити, соединяющей грузы, T = 150 Н. Определите длину нити l.



Решение.

Для каждого груза выберем инерциальную систему отсчёта, ось которой направлена вдоль штанги к оси вращения (см. рисунок), и запишем в проекциях второй закон Ньютона для грузов:

где   — центростремительные ускорения грузов,   —  угловая скорость вращения, R1 и R2 — радиусы окружностей.



Учитывая, что   и  , из записи второго закона Ньютона получим:

.

Подставляя значения физических величин, найдём длину нити: