Многократные. Обработка результатов прямых многократных измерений Примеры расч. Обработка результатов прямых многократных измерений. Примеры расчета
 Скачать 93.97 Kb. Скачать 93.97 Kb.
|
Решение.Расположим результаты наблюдений в порядке их возрастания, от 𝒙𝒎𝒂𝒙 до 𝒙𝒎𝒊𝒏 и найдем размах ряда 𝑳 = 𝒙𝒎𝒂𝒙 − 𝒙𝒎𝒊𝒏. Запишем вариационный ряд результатов многократных наблюдений xiв порядке возрастания (графа 2 табл.2). Определим оптимальное число интервалов по формуле Стерджесса: 𝒎 = 𝟑, 𝟑 ∙ 𝒍𝒈(𝒏) + 𝟏 Определим ширину интервала ∆𝒍, разделим размах ряда 𝑳 на mравных интервалов 𝒉 = (𝒙𝒎𝒂𝒙 − 𝒙𝐦𝐢𝐧 )⁄𝒎 = 𝑳/𝒎 = ∆𝒍 Изобразим полученные результаты графически, нанеся на ось абсцисс значения физической величины и обозначив границы интервалов (графа 5 табл.2), а на ось ординат – относительную частоту попаданий 𝒏𝒌/𝒏 (графа 7 табл. 2). Построив на диаграмме прямоугольники, основанием которых является ширина интервалов (𝒉 = ∆𝒍), а высотой 𝒏𝒌/𝒏 , получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте. На рис. 1 показана полученная в одном из опытов гистограмма, построенная на основании результатов 100 наблюдений, сгруппированных в таблице 3 (∆𝒍 – ширина интервала). Таблица 3 Результаты наблюдений
В данном опыте в первый и последующие интервалы попадает соответственно 0,06; 0,12; 0,18; 0,25; 0,17; 0,14 и 0,08 от общего количества наблюдений; при этом, очевидно, что сумма этих чисел равна единице. 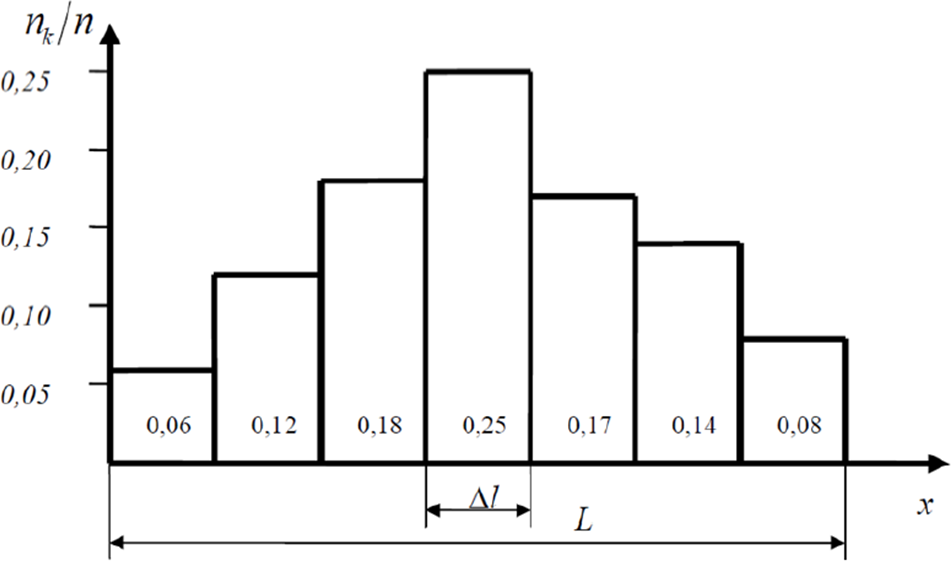 Рис.1. Гистограмма Данная в примере гистограмма позволяет предположить нормальный характер распределения результатов многократных наблюдений |
