Общественное здоровье. Методика изучения общественного здоровья. Организация медикосоциального исследования

• Название: Общественное здоровье. Методика изучения общественного здоровья. Организация медикосоциального исследования
• Дата: 07.12.2022
• Размер: 1.27 Mb.
• Имя файла: praktikum_po_3_kursu.doc
• Тип: Реферат; #832462
• страница: 5 из 8

Тема: Оценка достоверности результатов исследования. Стандартизация. Корреляция.

В результате изучения указанных тем студент должен знать: оценку достоверности статистических величин для относительных показателей, методику вычисления, использования и оценки; показания к применению метода стандартизации; значение стандартизированных показателей; определение функциональной и корреляционной связи; методику вычисления и оценки коэффициента корреляции, его практическое применение.

Студент должен уметь: вычислять и оценивать достоверность разности для относительных величин; вычислять и анализировать стандартизированные показатели по прямому методу и применять их для анализа материала; устанавливать и оценивать наличие корреляционной связи между изучаемыми признаками методом квадрантов.

Реферат темы

Оценка достоверности результатов исследования

Оценка достоверности статистических величин необходима, для того, чтобы по части явления можно было бы судить о явлении в целом и о его закономерностях.

Мерой достоверности показателя является его ошибка. показывающая. насколько результат. полученный при выборочном исследовании, отличается от результата, который мог бы быть получен при сплошном исследовании всей генеральной совокупности.

Средняя ошибка относительных величин определяется по формуле:

,

где: m_p – средняя ошибка показателя

q – основание – Р, т.е (100-Р) (1000-Р) и.т.д.;

n – общее число наблюдений.

При числе наблюдений менее 30 в формулу вводиться поправка:



P генеральной совокупности = Р выборочной совокупности ±tm, где t – критерий достоверности.

Достоверность разности между двумя относительными величинами определяется по формуле:

,

где: Р₁ и Р₂ – показатели, полученные при выборочных исследованиях; m₁ и m₂ – соответствующие ошибки.

Полученный критерий t оценивается по общепринятым правилам: если t ≥ 2, то разность следует считать достоверной, т.е. она соответствует вероятности безошибочного прогноза, равной 95% и более (Р ≥ 95% ). Если же t < 2, то разность недостоверна (Р < 95%). Это означает. что для выводов о достоверности разности необходим дополнительный материал.

При малом числе наблюдений (n < 30 в каждой группе) критерий достоверности оценивается с помощью специальной таблицы.

Решение типовой задачи

На нормальное развитие детей и состояние его здоровья большое влияние оказывают материально-бытовые факторы. Результаты проведенного исследования показали, что удельный вес малообеспеченых семей с низким доходом в многодетных семьях составляет 89,8%, а в семьях с 1-2 детьми – 12,1 %. В основной и контрольной группах было опрошено по 796 семей. Для доказательства того, что различие приведенных показателей не носит случайных характер, следует провести оценку достоверности их разницы.

Определите, есть ли статистически достоверная разница между показателями, характеризующими низкий доход семьи в основной и контрольной группах.

Алгоритм решения задачи

, где: Р – в %, q = 100 – Р, n – общее число наблюдений



Типовые задачи

Задача № 1. Определите, имеется ли статистически достоверная разница между летальностью в 2-х больницах города N. Известно, что число лечившихся в больнице № 1 было 4350, а летальность составила 4,5%; в больнице № 2 число лечившихся за год – 6760, а летальность равна 3,5%.

Задача № 2. Определите, имеется ли статистически достоверная разница между первичной заболеваемостью среди юношей и девушек обслуживаемых межвузовской поликлиникой. Первичная заболеваемость юношей составила 392,8‰, а девушек 510,3‰. Известно, что юношей – 467 человек, а девушек – 883 человек.

Задача № 3. Определите, имеется ли статистически достоверная разница между младенческой смертностью в основной и контрольной группах, если известно, что в основной группе младенческая смертность составила 21,8‰ (700 детей за год), а в контрольной группе 21,1‰ (300 детей за год).

Задача № 4. Определите, имеется ли статистически достоверная разница между показателями характеризующими рождаемость в семьях, имеющих детей с ВПР (основная группа), и семьями, не имеющими детей с ВПР (контрольная группа). Известно, что в основной группе рождаемость составила 3,8‰, а в контрольной 11,3‰. Изучалось 2730 семей и 2910 семей соответствующих групп.

Задача № 5. Произведенное исследование 2800 женщин основной группы и 2600 женщин контрольной группы показало, что 26,1 % из основной и 18,6% из контрольной группы рожали детей в возрасте от 20 до 30 лет. Определите, есть ли статистически достоверная разница между полученными показателями.

Метод стандартизации

Стандартизация – метод расчета условных (стандартизированных) показателей заменяющих интенсивные (или другие) величины в случаях, когда сравнение последних затруднено из-за несопоставимости состава групп.

Это достигается с помощью данного метода, а именно:

1. Метод стандартизации применяется для сравнения показателей, вычисленных в неоднородной по структуре среде. Стандартизация позволяет исключить влияние среды.

2. Сущность стандартизации заключается в вычислении обобщенных (стандартизированных) показателей.

3. Стандартизированные показатели характеризуют только соотношения, но не истинные размеры явления. Они являются условными и могут быть использованы только с целью сравнения.

Виды метода стандартизации

В настоящее время разработаны три основных метода стандартизации: прямой, косвенный, обратный.

Прямой метод применяется в том случае, если мы знаем состав среды и состав явлений. Косвенный метод применяется, когда известен состав среды, но не известен состав явлений или явления по изучаемому признаку выражено малыми цифрами. Обратный (косвенному) применяется, когда известен состав явления, но не известен состав среды.

Чаще используется прямой метод стандартизации. Рассмотрим методику вычисления стандартизированных коэффициентов по прямому методу на примере.

Прямой метод стандартизации состоит из 4-х последовательных этапов.

I этап – расчет общих интенсивных показателей по всем группам в двух сравниваемых совокупностях, то есть вычисление общих показателей.

II этап – определение стандарта. При прямом методе за стандарт берется состав среды. Выбор стандарта произвольный.

III этап – расчет ожидаемых величин в каждой группе стандарта.

IV этап – вычисление стандартизированных показателей.

Вычисление стандартизированных показателей осуществляется в 2 этапа:

1) Суммирование ожидаемых чисел.

2) Полученная сумма выражается в показателях (процент, промилли) по отношению к общему числу больных, указанному в итоговой строке стандарта.

Главная ценность стандартизированных показателей в том, что они обеспечивают возможность сравнения показателей в разных по составу совокупностях и позволяют получить ответ на вопрос о том, где выше или ниже величина изучаемого явления при условии исключения влияния на него неоднородного состава сравниваемых совокупностей.

Применение метода стандартизации в практике здравоохранения

Данный метод применяют для сравнения показателей смертности, летальности. заболеваемости часто вычисленных для неоднородных по своему возрастному или половому составу групп населения. Эта неоднородность влияет на величину показателя.

Решение типовой задачи

В ходе исследования было выявлено, что удельный вес часто и длительно болеющих детей (ЧДБ) в многодетных семьях составил 31,0%, а в семьях с 1-2 детьми 21,0%. Однако, в основной группе было значительно больше малообеспеченных семей (89,8% против 12,1%) и меньше семей с высоким материальным доходом.

Распределение семей по материальному доходу, количеству детей в каждой их групп и количеству часто и длительно болеющих детей:

№ п/п	Доход семьи	Основная группа		Контрольная группа
		Всего детей	ЧДБ	Всего детей	ЧДБ
1	Низкий	715	224	96	34
2	Средний	73	22	619	124
3	Высокий	8	1	81	9
	ИТОГО	796	247	796	167

Определите, отличалось бы количество часто и длительно болеющих детей в основной и контрольной группах, если бы не наблюдались различия в материальных доходах многодетных семей и в семьях с 1 - 2 ребенком.
Алгоритм решения задачи

Доход семьи	Основная группа			Контрольная группа			стандарт	Ожидаемое число ЧБД
	Всего детей	ЧДБ	Удельный вес ЧДБ %	Всего детей	ЧДБ	Удельный вес ЧДБ %		Основная группа	Контрольная группа
Низкий	715	224	31,3	96	34	35,4	405,0	126,9	143,6
Средний	73	22	30,1	619	124	20,0	346,0	104,2	69,2
Высокий	8	1	12,5	81	9	11,1	44,5	5,6	4,9
ИТОГО	796	247	31,0	796	167	21,0	796	236,7	217,7

29,7% 27,4%

кол-во ЧДБ 224

I этап. Удельный вес ЧДБ детей = ^{____________________} х100% = ^______х100% =31,3% всего детей 715

II этап. За стандарт принимается полусумма детей.

всего детей основной группы + всего детей контрольной группы 715+96

Стандарт = ^{______________________________________________________________________} = ---------=405,5 2 2

удельный вес ЧБД х стандарт 31,3 х 405,5

III этап. Ожидаемое число ЧДБ = ^{______________________________} = ^{________________} = 126,9

основание (100, 1000) 100

Строка ИТОГО для ожидаемого числа ЧДБ рассчитывается суммированием вышеуказанных строк (приме, 126,9 + 104,2 + 5,6 = 236,7)

IV этап.

Стандартизированный ожидаемое число ЧДБ 236,7

показатель удельного веса = ^{____________________________} х 100 = ^____________х100= 29,7%

ЧДБ основной группы стандарт 796
Стандартизированный 217,7

показатель удельного веса = ^__________х100 = 27,4%

ЧДБ контрольной группы 796
Показатель наглядности: 29,7% - 100%

27,4% - Х% Х = 92,3% 100% - 92,3% = 7,7%

ВЫВОД: если поставить в равные условия по материальному доходу многодетные семьи и семьи с 1-2 детьми, то удельный вес ЧДБ детей в основной группе на 7,7% выше, чем в контрольной (основная группа 29,7%, контрольная 27,4%)

Типовые задачи

Задача № 1. Вычислите стандартизированные показатели заболеваемости болезнями печени и желчевыводящих путей рабочих двух цехов и сравнить их с показателями заболеваемости, вычисленными обычным путем.

Распределение рабочих двух цехов и числа больных по полу:

Пол	Цех №1 Число рабочих	Число больных	Цех №1 Число рабочих	Число больных
Мужчины	421	13	390	13
Женщины	635	43	320	23
ВСЕГО	1056	56	710	36

Задача № 2. Вычислите стандартизированные показатели послеоперационной летальности при непроходимости кишечника в больницах А и Б и сравнить их с показателями летальности вычисленными обычным путем.

Распределение больных с непроходимостью кишечника из числа умерших от этого заболевания в больницах А и Б по срокам поступления в стационар от начала заболевания:

Сроки поступления в стационар от начала заболевания	Больница А		Больница Б
	Число больных	Число умерших	Число больных	Число умерших
До 6 часов	350	42	170	20
От 6 до 24 часов	273	49	215	37
Свыше 24 часов	104	30	418	116
ВСЕГО	727	121	803	173

Задача № 3. Проведите стандартизацию показателей смертности городского и сельского населения по прямому методу. За стандарт возьмите возрастной состав населения всей области.

Возраст в годах	Городское население		Сельское население
	Численность населения	Число умерших	Численность населения	Число умерших
До 15 лет	9795	152	22651	369
15-49	10269	82	29385	94
50 и старше	3716	85	9183	187
ВСЕГО	23780	319	61220	650

Задача № 4. Вычислите стандартизированные показатели инфицированности детей. раннего возраста, воспитывающихся в яслях, и детей, воспитывающихся дома.

Возраст	Дети, воспитывающиеся в яслях		Дети, воспитывающиеся дома
	Число детей	Из них инфицированных	Число детей	Из них инфицированных
До 1 года	50	4	110	10
От 1 года до 3 лет	75	6	100	9
От 3 до 4 лет	200	25	90	12
ВСЕГО	325	35	300	31

Задача № 5. Вычислить стандартизированные показатели обращаемости юношей и девушек в межвузовские поликлиники.

ВУЗы	Девушки		Юноши
	Число студентов	Кол-во обращений	Число студентов	Кол-во обращений
Технический	164	186	286	200
Медицинский	336	478	114	142
Гуманитарный	323	349	133	127
ВСЕГО	823	1013	533	469

Метод корреляции

Различают 2 формы связи: функциональную и корреляционную.

Функциональная связь отражает строгую зависимость процессов или явлений; изменение какого-либо одного явления обязательно связано с изменением другого явления на определенную величину (объем газа и давление). Эта связь характерна для физико-химических процессов.

Корреляционная связь – связь между явлениями, проявляющаяся не в каждом отдельном случае, а при массовом сопоставлении рассматриваемых признаков.

Характер и теснота связи измеряется коэффициентом корреляции (r_xy). По направлению связь бывает прямая и обратная.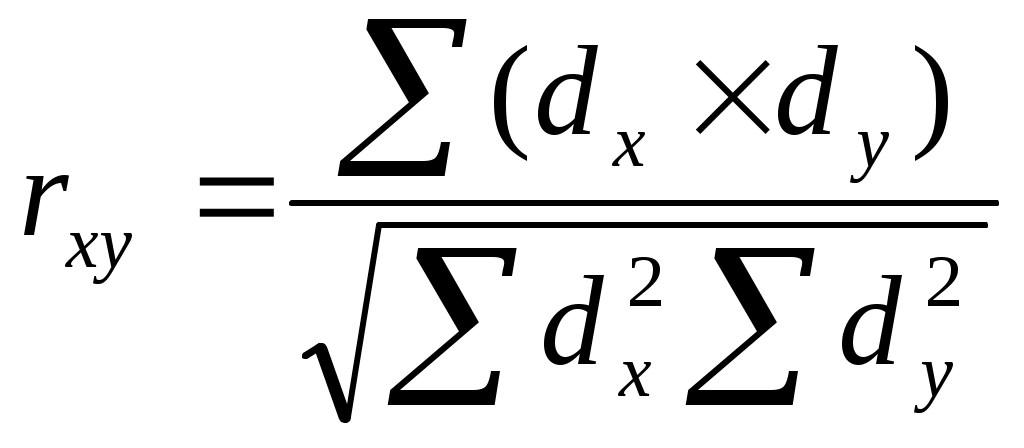



Прямая связь (положительный коэффициент корреляции): с увеличением (уменьшением) одного признака увеличивается (уменьшается) другой признак.

Обратная связь (отрицательный коэффициент корреляции): с увеличением одного признака (явления) другой уменьшается.

Теснота определяется величиной коэффициента корреляции от 0 до ± 1.

Определение тесноты и направления связи по коэффициенту корреляции

Оценка корреляции	Величина коэффициента при наличии
	Прямой корреляции (+)	Обратной (-)
Связь отсутствует	0	0
Малая (низкая, слабая)	От 0 до +0,3	От -0,3 до 0
Средняя	От +0,3 до +0,7	От -0,3 до -0,7
Большая (высокая, сильная)	От +0,70 до +1,0	От -0,7 до -1,0
Полная связь	+1,0	-1,0

Корреляционная связь может быть прямолинейной и криволинейной.

Прямолинейная связь – характеризуется относительно равномерным изменением средних значений одного признака при равных изменениях другого.

Криволинейная связь – при равномерном изменении одного признака могут наблюдаться возрастающие и убывающие значения другого признака.

Существуют следующие методы вычисления коэффициентов корреляции: рангов, квадратов, путем составления корреляционной решетки.

Решение типовой задачи

Медико-социальное обследование матерей основной и контрольной групп позволило установить, что в акушерско-гинекологическом анамнезе у матери с 1 ребенком – 1,8 аборта, с 2 детьми – 1,6 аборта, с 3 детьми – 1,9 аборта, с 4 детьми – 3,8 аборта, с 5 детьми – 3,9 аборта, с 6 детьми – 4,1 аборта, с 7 детьми – 3,9 аборта, с 8 детьми – 4,2 аборта, с 9 детьми – 5,0 аборта, с 10 детьми – 5,0 аборта.

Необходимо установить имеется ли связь между количеством детей в семье и числом абортов у матерей.

Алгоритм решения задачи

Корреляционная зависимость между количеством детей в семье и количеством абортов у матери.

Кол-во детей в семье, Х	Кол-во абортов у матерей, Y	dx	dy	dx2	dy2	dx x dy
1	1,8	-4,5	-1,7	20,25	2,89	7,65
2	1,6	-3,5	-1,9	12,25	3,61	6,65
3	1,9	-2,5	-1,6	6,25	2,56	4,0
4	3,8	-1,5	0,3	2,25	0,09	-0,45
5	3,9	-0,5	0,4	0,25	0,16	-0,2
6	4,1	0,5	0,6	0,25	0,36	0,3
7	3,9	1,5	0,4	2,25	0,16	0,6
8	4,2	2,5	0,7	6,25	0,49	1,75
9	5,0	3,5	1,5	12,25	2,25	5,25
10	5,0	4,5	1,5	20,25	2,25	6,75
MX = 5,5	MY = 3,5			∑ dx2=82,5	∑dy2=14,82	∑ (dxx dy)=32,45

d_x = X - M_X, например, d_x =1–5,5 = -4,5 d_y = Y - M_Y



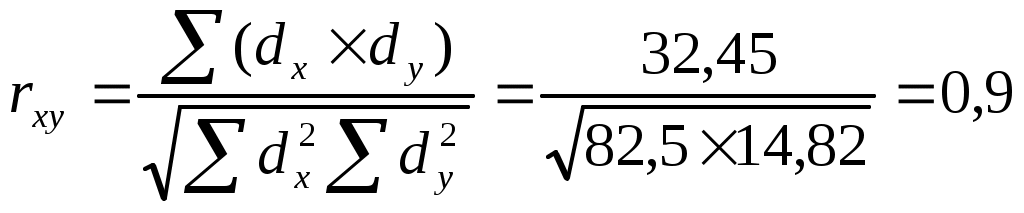ВЫВОД: чем больше детей в семье, тем больше количество абортов у матерей. Связь прямая, сильная.

Типовые задачи

Задача № 1. Определить влияние введения сыворотки на летальность при дифтерии, если известно, что при введении сыворотки в первый день летальность составляет 2%, во второй день – 4%, третий день - 6%. четвертый день – 8%, пятый день -16%.

Задача № 2. Определить характер и силу связи между возрастом и весом студентов, используя приведенные данные: 22 года – 56 кг, 22 года – 57 кг, 21 год – 59 кг, 24 года – 60 кг, 23 года – 63 кг, 23 года – 65 кг, 24 года – 67 кг, 23 года – 72 кг, 24 года – 79 кг, 24 года – 82 кг.

Задача № 3. Определить характер и размер связи между удельным весом регулярно курящих девочек и классом школы, в котором она учатся. Установлено, что среди 5-класниц регулярно курит 0,4%, среди 6-класниц – 1,1%, 7-класниц – 3,9%, 8-класниц – 8,1%, 9-класниц – 8,4%, 10-класниц – 18,1%, 11-класниц – 19,7%.

Задача № 4. Заболеваемость инфарктом миокарда мужчин по возрастным группам в городе N составила: в 40 лет – 0,33‰, в 45 лет – 1,3‰, в 50 лет – 1,5‰, в 55 лет – 2,0‰, в 60 лет – 6,2‰, в 65 лет – 6,0‰. Определить наличие. величину и направление связи между возрастом и заболеваемостью.

Задача № 5. Имеется ли связь между возрастом дошкольников посещающих ДДУ и их ростом. Средний рост в 3 года - 94,8 см, в 4 года -100,5 см, в 5 лет – 106,9 см, в 6 лет – 112,7 см, в 7 лет – 118,3 см.

Контрольные вопросы

1. 
   Для чего необходима оценка достоверности результатов исследования?
   
2. 
   Определение каких величин предусматривает оценка достоверности результатов исследования?
   
3. 
   По какой формуле рассчитывается средняя ошибка относительных величин?
   
4. 
   Что такое доверительные границы в генеральной совокупности, как они определяются?
   
5. 
   Как определяется достоверность разницы между показателями выборочных совокупностей?
   
6. 
   Какое значение критерия t свидетельствует о достоверности различий между показателями?
   
7. 
   В каких случаях применяется метод стандартизации?
   
8. 
   Что такое стандартизация?
   
9. 
   Какие методы стандартизации существуют?
   
10. 
    Перечислите этапы прямого метода стандартизации.
    
11. 
    Какие показатели характеризуют истинный уровень явлений, стандартизированные или нестандартизированные?
    
12. 
    Для чего практическому врачу необходимо знать метод корреляции?
    
13. 
    Какие две формы количественных связей между явлениями или процессами различают?
    
14. 
    Что понимают под функциональной связью?
    
15. 
    Что понимают под корреляционной связью?
    
16. 
    Охарактеризуйте корреляционную связь по направлению.
    
17. 
    Что понимают под силой корреляции? Как она определяется?
    
18. 
    Какие способы расчета коэффициента корреляции существуют?
    
19. 
    Какая методика расчета коэффициента корреляции способом квадратов?
    
20. 
    В каких случаях производится расчет коэффициента корреляции методом квадратов?
    

Список рекомендуемой литературы

1. 
   Юрьев В.К, Куценко Г.И. «Общественное здоровье и здравоохранение». – Санкт-Петербург, ООО Издательство «Петрополис», 2000. – 914 с. Стр. 197-204.
   
2. 
   «Социальная медицина и организация здравоохранения»,/ Руководство для студентов, клинических ординаторов и аспирантов в 2х томах./ Т 1. В.А.Миняев, Н.И.Вишняков, В.К.Юрьев, В.С. Лучкевич.- СПб.. Издательство «Водолей», 1998г. Стр 167-173, 140-148.
   
3. 
   Медик В.А., Юрьев В.К. «Курс лекций по общественному здоровью и здравоохранению. Часть I. Общественное здоровье». – М.: Медицина, 2003. – 368с.: ил. – ISBN 5-225-04122-1. Стр.325-330, 345-358
   
4. 
   «Общественное здоровье и здравоохранению» учебник для студентов./Под редакцией В.А.Миняева, Н.И. Вишнякова. – М.:Медпресс-информ, 2002. Стр108-112, 86-92
   
5. 
   Юрьев В.К «Здоровье населения и методы его изучения». Учебное пособие ППМИ, СПб. 1993. – 192с. Стр. 117-1213
   
6. 
   «Методические указания к лабораторным занятиям по медицинской статистики для студентов IV курса» Под редакцией д.м.н. профессора И.Т.Леонова. ЛПМИ, Л 1984г. с 64. Стр. 15-16, 25-27,39-40.
   

Занятие № 6