Теория оптимизаций. ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций. Общие сведения о теории оптимизации
 Скачать 2.93 Mb.
|
|
В других случаях (B2– АС = 0,разные знаки у А и С и т.д.) никакого заключения о характере стационарной точки сделать нельзя и требуется дополнительное исследование. Пример 2. В примере 1 было установлено, что функция z=2x3+xy2+5x2+ y2 согласно решению системы уравнений
имеет четыре стационарные точки:
Вторые частные производные данной функции равны
В точке M1имеем: А = 10, В = 0, С = 2. Здесь В2– АС= – 20 <0; значит, точка М1 является точкой экстремума, и так как А и С положительны, то точкой минимума. В точке М2 (т.к. А = –10, В = 0, С = –  иВ2 – АС < 0) тоже точка экстремума, но ввиду того, что А и С отрицательны, это точка минимума.Нетрудно проверить, что точки М3и M4 не являются точками экстремума (в них В2 – АС > 0). Пример 3. Найдем точки экстремума функции z=x2 – y2. Приравнивая частные производные  нулю, находим одну стационарную точку – начало координат.
3 Задачи о наибольших и наименьших значениях Пусть требуется найти наибольшее и наименьшее значение функции z = f (x,у) в некоторой области (рассматриваемой вместе со своей границей). Если какое-либо из таких значений достигается функцией внутри области, то оно, очевидно, является экстремальным. Но может случиться так, что наибольшее или наименьшее значение принимается функцией в некоторой другой точке, лежащей на границе области. Из сказанного следует правило: Для того чтобы найти наибольшее или наименьшее значение функцииz = f(x, у) в замкнутой области, нужно найти все максимумы или минимумы функции, достигаемые внутри этой области, а также наибольшее или наименьшее значение функции на границе области. Наибольшее из всех этих чисел и будет искомым наибольшим значением, а наименьшее – наименьшим.
Возьмем на плоскости какую-нибудь точку Р (х, у). Cумма квадратов её расстояний до заданных точек Р1 , Р2 , Р3 , обозначаемая через z ,выражается так: z = (x–0)2+(y–0)2+(x–1)2+(y–0)2+(x–0)2+(y–1)2 или z = 3x2 + 3y2 – 2x – 2y + 2. Задачу целесообразно декомпозировать на две части. Первая часть задачи сводится к нахождению наименьшего значения этой функции во всей плоскости, вторая часть – к нахождению наибольшего значения функции при условии, что точка Р(х,у)принадлежит замкнутой области D, ограниченной треугольником Р1 Р2 Р3. Найдем экстремумы функции z = 3x2 + 3y2 – 2x – 2y + 2. Приравнивая производные  и  к нулю, из уравнений получаем ,  .Значит, существует лишь одна стационарная точка Р(  , ).Вместе с тем, во всей плоскости функция не имеет наибольшего значения, так как ясно, что существуют точки, для которых указанная сумма больше любого наперёд заданного числа. А так как, с другой стороны, очевидно, что эта сумма должна достигать наименьшего значения, то именно стационарная точка Р только и может быть точкой, в которой функция получает свое наименьшее значение, равное z( , ) = 3 + 3 – 2· – 2· +2= 1 .Переходим ко второй части задачи. Вследствие того, что заданная функция не имеет максимума, её наибольшим значением в области Dявляется наибольшее из значений, принимаемых на границе, т. е. на сторонах треугольника, образуемого точками P1 (0, 0), Р2 (1, 0), Р3 (0, 1). На стороне Р1 Р2имеем у=0. При этом z= 3x2 + 3y2 – 2x–2y+2= 3x2 – 2x+2 и эта функция достигает в интервале [0, 1] наибольшего значения, равного 3, при х=1,т. е. в точке P2 . На стороне Р1 Р3имеем х=0.При этом z= 3x2 + 3y2 – 2x–2y+2= = 3y2 – 2y + 2, и функция достигает в интервале [0, 1] наибольшего значения, также равного 3 при у = 1, т. е. в точке Р3 . Наконец, на стороне Р2 Р3имеем х + у = 1, при этом z = 3x2 + 3(1 – x)2 – 2x – 2(1 – x) + 2 = 6x2 – 6x + 3, и такая функция в интервале [0, 1] изменения x достигает наибольшего значения, равного 3, при х=1.То есть наибольшее значение на стороне Р2 Р3функция zполучает в тех же точках Р2и Р3. Таким образом, из решения второй части задачи следует, что искомых точек треугольника (сумма квадратов расстояний которых от вершин Р1 Р2 Р3имеет наибольшее значение) имеется две: Р2и Р3. ЛИТЕРАТУРА 4 А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа. М: Изд-во «Наука», 2005 (50 экз.). ВОПРОСЫ ДЛЯ САМОКОТРОЛЯ 7) Безусловный экстремум функции двух переменных: определение и необходимые условия экстремума с доказательством и геометрической интерпретацией 8) Стационарные точки функции двух переменных: понятие и виды. Найти точки экстремума функции z=x2 – y2. 9) Задачи о наибольших и наименьших значениях. Найти точку на плоскости Оху, сумма квадратов расстояний которой до трёх точек P1 (0, 0), Р2 (1, 0), Р3 (0, 1) имеет наименьшее значение, и точку треугольника с вершинами в Р1 , Р2 , Р3 , сумма квадратов расстояний которой до вершин имеет наибольшее значение. 10) Наибольшее и наименьшее значения функции в замкнутой области с иллюстрацией на примере нахождения точки на плоскости Оху, сумма квадратов расстояний которой до трех точек P1 (0, 0), Р2 (1, 0), Р3 (0, 1) имеет наименьшее значение, и точки треугольника с вершинами в Р1 , Р2 , Р3 , сумма квадратов расстояний которой до вершин имеет наибольшее значение. Лекция 2.2 Условные экстремумы При отыскании экстремумов функций нескольких переменных часто возникают задачи, связанные с так называемым условным экстремумом. Разъясним это понятие на примере функции двух переменных. Пусть задана функция z = f (x,у)и линия Lна плоскости Оху. Задача состоят в том, чтобы на линии Lнайти такую точку Р(х,у), в которой значение функции f (x,y)является наибольшим или наименьшим по сравнению со значениями этой функции в точках линии L, находящихся вблизи точки Р. Такие точки Рназываются точками условного экстремума функции f (x,y) на линии L. В отличие от обычной точки экстремума значение функции в точке условного экстремума сравнивается со значениями функции не во всех точках некоторой ее окрестности, а только в тех, которые лежат на линии L. Совершенно ясно, что точка обычного экстремума (говорят также безусловного экстремума) является и точкой условного экстремума для любой линии, проходящей через эту точку. Обратное же, разумеется, неверно: точка условного экстремума может и не быть точкой обычного экстремума. Поясним сказанное примером.
значение функции достигается в точке Р(  , ), лежащей посередине между точками Аи B.Точке условного экстремума (максимума) функции  на рассматриваемой линии соответствует точка М1на полусфере, и из рисунка видно, что ни о каком обычном экстремуме здесь не может быть речи.Отметим, что при отыскании наибольшего и наименьшего значений функции в замкнутой области (см. заключительную часть примера 4) приходится находить экстремальные значения функции на границе этой области, то есть на какой-то линии, и тем самым решать задачу на условный экстремум. Приступим теперь к практическому отысканию точек условного экстремума функции z = f (x,y)при условии, что переменные x и усвязаны уравнением φ (x,y) = 0. Это последнее соотношение будем называть уравнением связи. Если из уравнения связи у можно явно выразить через х: y = ψ (x), то, подставляя в выражение функции z = f (x,у)вместо у функцию ψ (x), мы получим функцию одной переменной z = f (x, ψ (x))=Ф(x). Найдя значения х, при которых эта функция достигает экстремума, и определив затем из уравнения связи соответствующие им значения у, мы и получим искомые точки условного экстремума. Так в вышеприведенном примере из уравнения связи х + у – 1 = 0 имеем у =1 – х. Отсюда  .Легко проверить, что zдостигает максимума при х = 0,5; но тогда из уравнения связи у = 0,5, и мы получаем как раз точку Р, найденную из геометрических соображений. Очень просто решается задача на условный экстремум и тогда, когда уравнение связи можно представить параметрическими уравнениями: x = x(t), y = y(t). Подставляя выражения для хи ув данную функцию, снова приходим к задаче отыскания экстремума функции одной переменной. Если уравнение связи имеет более сложный вид и нам не удается ни явно выразить одну переменную через другую, ни заменить его параметрическими уравнениями, то задача отыскания условного экстремума становится более трудной. Будем по-прежнему считать, что в выражении функции z= f(x,y)переменная у является функцией от х, определенной неявно уравнением связи φ (x,y) = 0. C учётом того, что согласно правилу дифференцирования неявной функции 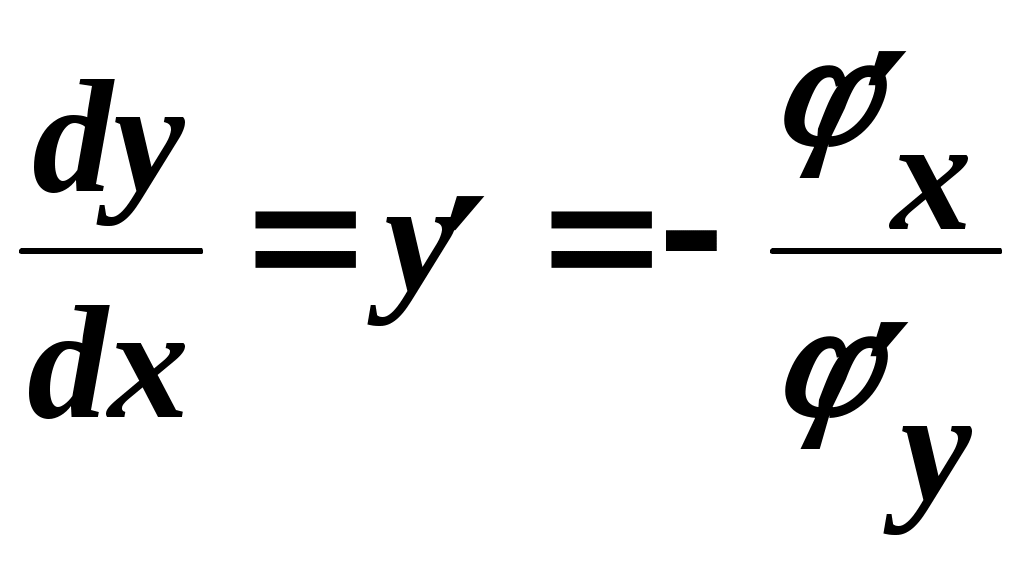 ), полная производная от функции z = f (x,y)по x равна .В точках условного экстремума найденная полная производная должна равняться нулю – это дает одно уравнение, связывающее x и у, а с учётом уравнения связи получаем систему двух уравнений с двумя неизвестными 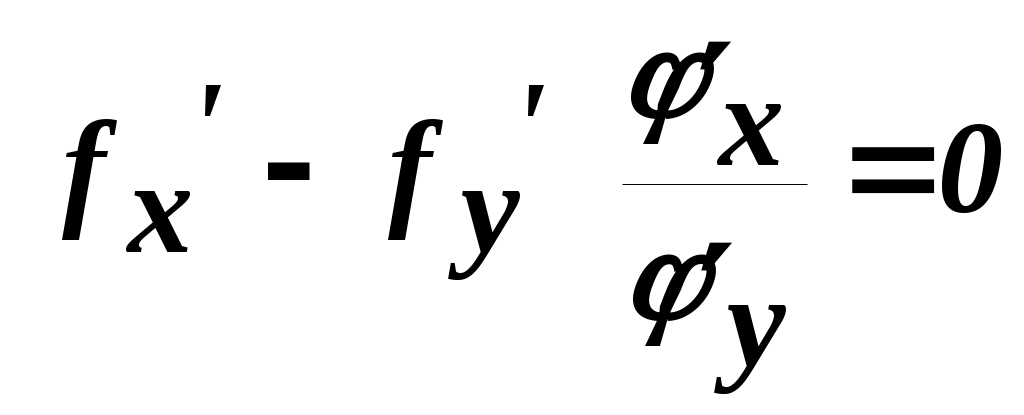 , φ (x,y) = 0.Преобразуем эту систему к гораздо более удобной, записав первое уравнение в виде пропорции и введя новую вспомогательную неизвестную λ: 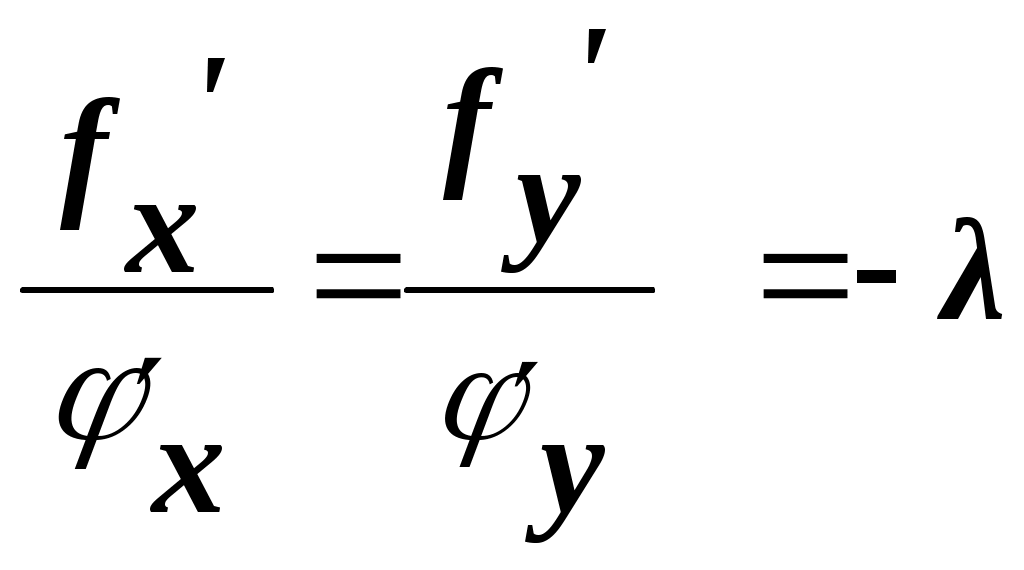 (*)(знак минус перед λ. поставлен для удобства). От этих равенств легко перейти к следующей системе:   которая вместе с уравнением связи φ (x,y) = 0 образует систему трех уравнений с тремя неизвестными х, уи λ. С учётом изложенного может быть сформулировано следующее правило: для того чтобы найти точки, которые могут быть точками условного экстремума функции z = f (x,y) при уравнении связи φ (x,y) = 0, нужно образовать вспомогательную функцию  где λ – некоторая постоянная и, вычислив производные функции, составить уравнения для отыскания точек экстремума этой функции.Указанная система уравнений описывает, как обычно, только необходимые условия, т. е. не всякая пара значений хиу, удовлетворяющая этой системе, обязательно является точкой условного экстремума. Достаточные условия для точек условного экстремума мы приводить не будем; очень часто конкретное содержание задачи само подсказывает, чем является найденная точка. Описанный прием решения задач на условный экстремум называется методом множителей Лагранжа. Метод Лагранжа имеет наглядный геометрический смысл, который мы сейчас и выясним. Предположим, что на рис. 4.2 изображены линии уровня функции z = f (x,y)и линия L, на которой отыскиваются точки условного экстремума.
пересекает соответствующую линию уровня, и лежит по одну сторону от неё. В такой точке линия Lи линия уровня f (x, y) = Скасаются друг друга (предполагается, что линии гладкие) и угловые коэффициенты касательных к ним должны быть равны. Из уравнения связи φ (x,y) = 0(по правилу дифференцирования неявной функции) имеем у' = –  / , а из уравнения линии уровня f (x, y) = С соответственноу' =– / Приравнивая производные и произведя простейшее преобразование, получаем уравнения (*).Приведенное рассуждение может потерять силу, если линия уровня такова, что во всех ее точках  ,  (например, функция z=4 – х2и линия уровня х = 0,отвечающая значению z = 4) – в знаменателе у' =– / получается ноль.Пример 5. Найти наибольшее значение функции z = xy,если хи y положительны и подчиняются уравнению связи  =0.Здесь уравнение связи простое (оно представляет эллипс) и можно было бы сразу прийти к отысканию экстремума функции одной переменной, выразив учерез x или взяв параметрические уравнения эллипса. Мы же для иллюстрации решим пример методом Лагранжа. Составим вспомогательную функцию Ф (х, у) = xy+λ ( ).Приравнивая частные производные по хи по у нулю, получим  Исключая λ, приходим к уравнению 4у2– х2 = 0,решая которое совместно с уравнением связи находим х = 2и y = 1 (по условию задачи xи уположительны). Функция z = xyпри рассматриваемых значениях хи уположительна и в точках пересечения эллипса с осями координат (  ,0) и (0, )равна нулю. Поэтому найденная единственная точка Р(2, 1) будет точкой условного максимума; в этой точке zmax = 2. Легко проверить, что в точке Рэллипс касается линии уровня функции z = xy,проходящей через эту точку, т. е. гиперболы ху = 2.Задачи на условный экстремум для функций трех переменных допускают большее разнообразие. Пусть задана функция u= f (x,y,z)и переменные х, у и z связаны одним уравнением φ(х, у, z) = 0; это есть уравнение некоторой поверхности. Тогда точка условного экстремума является такой точкой поверхности, в которой функция принимает наибольшее или наименьшее значение по сравнению с ее значениями во всех близлежащих точках этой же поверхности. Можно искать условный экстремум функции f (x,y,z)и при двух уравнениях связи: φ1 (x,y,z) = 0 и φ2 (x,y,z)=0, которые определяют линию пересечения поверхностей в пространстве. Таким образом, задача сводится к отысканию такой точки линии, в которой функция принимает экстремальное значение, причем сравниваются значения функции только в точках рассматриваемой линии. Метод множителей Лагранжа в случае двух уравнений связи применяется следующим образом: строим вспомогательную функцию Ф (х, у,z) = f (x,y,z)+λ1 φ1(x,y,z)+λ2 φ2(x,y,z), где λ1 и λ2 – новые дополнительные неизвестные, и составляем систему уравнений для отыскания экстремумов этой функции    Добавляя сюда два уравнения связи, получаем систему пяти уравнений с пятью неизвестными х , у , z , λ1 , λ2. Искомыми точками условного экстремума могут быть только те, координаты х, у,zкоторых являются решениями этой системы. В самом общем виде задача ставится гак: требуется найти экстремумы функции ппеременных u = f(x, у, z,...,t)при условии, что эти переменные подчинены туравнениям связи (т < п):   …,  Вспомогательная функция зависит от ппеременных и содержит тдополнительных неизвестных  Уравнения для отыскания точек экстремума этой функции и уравнения связи составят систему m+nуравнений, из которой определяются координаты х,у,z, ..., t возможных точек условного экстремума. Пример 6. Найти прямоугольный параллелепипед наибольшего объема, если его полная поверхность равна заданной величине S. Обозначим стороны параллелепипеда через х, у, z.Тогда требуется найти наибольшее значение функции V = xyzпри условии, что 2ху+2yz+2zx=S. Вспомогательная функция Ф(x,y,z)=xyz + λ(xy+yz+zx). Уравнения для отыскания точек экстремума этой функции имеют вид    Вычитая эти уравнения друг из друга, получим    Отсюда ясно, что x=y= z,т. е. что искомый параллелепипед – куб. Размеры его определим из уравнения связи:  ,  .Пример 7. Найти наибольшее расстояние от начала координат до точек линии пересечения параболоида вращения z = x2+y2с плоскостью х+2у–z =0 (наименьшее расстояние равно нулю, так как линия пересечения проходит через начало координат). Расстояние r от начала координат до точки (x,у,z)равно  . Наибольшие значения корня и подкоренного выражения достигаются в одной и той же точке; поэтому будем искать условный максимум функции u= х2 +y2+z2 при двух уравнениях связиφ1(x,y,z)  ; φ2(x,y,z) .Составляя вспомогательную функцию  и приравнивая нулю ее частные производные, получим    Выразим отсюда координаты х, y, zчерез вспомогательные неизвестные (  и  )   Подставляем x, y и z в уравнения связи: 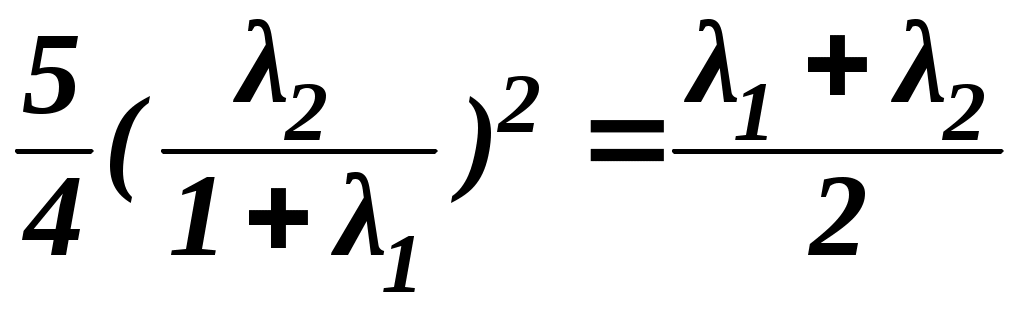 ,  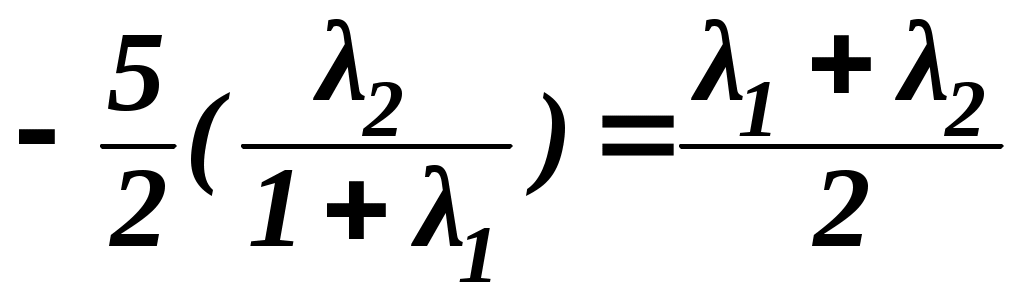.Приравнивая левые части обоих уравнений, получаем квадратное уравнение относительно  . Его первый корень =0приводит к значениям λ1 = 0 и λ2 = 0; им соответствует начало координат – точка минимума. Второй корень равен = –2. Даже не отыскивая λ1и λ2, находим х = 1, у = 2иz = x2+y2= 5. Ясно, что эта точка наиболее удалена от начала координат, и rmax= = .По данной теме предусмотрена лабораторная работа. Индивидуальные задания будут выданы с началом лабораторного занятия, на котором следует иметь микрокалькуляторы или устройства, выполняющие их функции. ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА 4 А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа. М: Изд-во «Наука», 2005 (50 экз.). ВОПРОСЫ ДЛЯ САМОКОТРОЛЯ 11) Условный экстремум функции двух переменных: понятие и отличие от безусловного экстремума с графической иллюстрацией, понятие уравнения связи. Найти наибольшее значение функции z = xy, если х и y положительны и подчиняются уравнению связи =0.12) Правило нахождения точек, которые могут быть точками условного экстремума функции двух переменных с обоснованиями (метод множителей Лагранжа с графической иллюстрацией) 13) Отыскание методом множителей Лагранжа экстремумов функции трёх переменных с иллюстрацией на примере нахождения наибольшего расстояния от начала координат до точек линии пересечения параболоида вращения z = x2+y2с плоскостью х+2у–z =0 |
, 0), M3 ( –1, 2), M4 ( –1, –2 ).
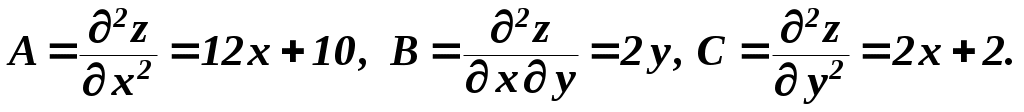
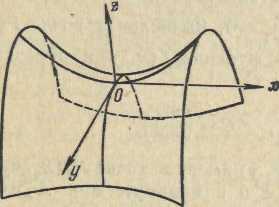
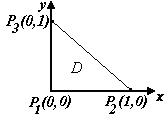Рис. 3.3
