Теория оптимизаций. ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций. Общие сведения о теории оптимизации
 Скачать 2.93 Mb.
|
|
Тема 3. ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ При подготовке двух лекций по данной теме использованы теоретические положения и примеры, заимствованные из учебно-методического пособия заведующей кафедры математики Ростовского военного института ракетных войск (РВИ РВ) Абаниной Т.И. Высшая математика. Основы вариационного исчисления. РВИ РВ 2003 Лекция 3.1 Основные понятия вариационного исчисления 1 Функционал, его вариации и приращения Вариационное исчисление – раздел математики, в котором изучаются методы отыскания экстремальных значений функционалов. Понятие функционала, является обобщением понятия функции. Функционал – это функция, аргумент которой – также функция. Задание функционала J(y(x)) равносильно заданию закона, по которому каждой функции y(x) из некоторого класса функций ставится в соответствие определённое число. Например,  пр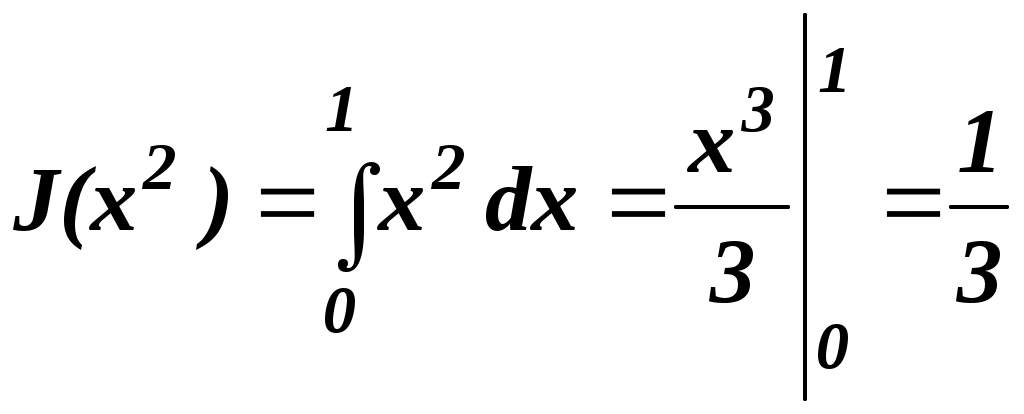едставляет собой функционал, значениями которого являются:при 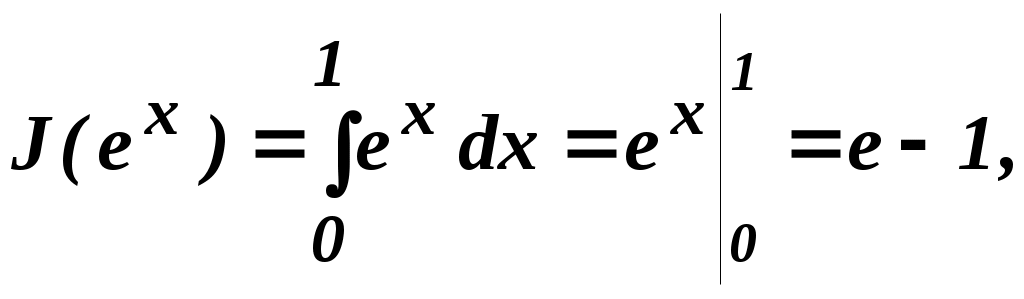 , равное  ;при  равное  …Физическая сущность функционала может быть различной – длина, время, напряженность электрического поля и т.д. Рассмотрим два конкретных примера задач вариационного исчисления. Пример 1. Найти в плоскости линию, соединяющую две заданные точки и имеющую наименьшую длину. Исследуемый функционал, для которого требуется найти наименьшее значение – длина линии. Задаваемый класс функций описывает множество линий, соединяющих заданные точки. Пример 2. Найти замкнутую кривую данной длины, ограничивающую наибольшую площадь. Исследуемый функционал, для которого ищется наибольшее значение – площадь фигуры. Рассматриваемый класс функций описывает множество кривых заданной длины. Функционал, определяемый на некотором задаваемом классе функций y(x), может рассматриваться в различных нормированных пространствах. Нормированное пространство С (n) [a,b], где 0≤n≤N, характеризуется так называемой нормой, которая для функции y(x) при изменении аргумента x в пределах отрезка [a,b]определяется равенством ║y║  = + +  .Частные случаи нормированного пространства С (n) [a,b] соответствуют различным значениям n: n = 0 соответствует пространству С (0)[a,b] функций (в более простом обозначении С[a,b]), непрерывных на отрезке [a,b],с нормой ║y║  = ;n = 1 соответствует пространству С (1) [a,b] функций, непрерывно дифференцируемых на отрезке [a,b]с нормой ║y║  = + ,и т.д., вплоть до ║y║  =   , где0≤n≤N.В нормированном пространстве вводится понятие расстояния  между функциями  и  , которое определяется как ║y2 – y1║ =  .Пример 3. Вычислить расстояние между функциями  и  в пространстве С[0,2].По определению,  = = .При исследовании функции  на экстремум в открытом интервале (0,2) получаем ;  0 при x = ±1. Но, x = – 1  (0,2). В отличие от этого, x = 1 (0,2), а с учётом того, что  и  (1) < 0, исследуемая функция в точке x = 1 достигает максимума, равного f (1) = 3·1– 13 = 2.Так как на концах закрытого интервала [0,2] значение функции f(0) = 0 и f(2) = –2, то приходим к окончательному выводу, что выражение  имеет максимум, и принимает в точках x = 1 и x = 2 наибольшее на отрезке [0,2] значение, равное по абсолютной величине 2.С учётом этого, расстояние между функциями y1=x3 и y2=3x в пространстве С[0,2] равно 2. Перейдём к рассмотрению других важных понятий, относящихся к теории вариационного исчисления. Пусть  – функционал относительно y(x).Приращением или вариацией аргумента y функционала называется разность  , где  – близкая к функции  рассматриваемого класса.Приращением функционала , соответствующим приращению  аргумента y, называют величину  ,представляющую изменение значения функционала с переходом от функции-аргумента y к значению  близкой функции.Если приращение функционала можно представить следующим образом  (║ ║),где  – линейная относительно часть приращения, а  (║ ║) – бесконечно малая более высокого порядка, чем ║ ║, то главную часть приращения  линейную относительно , то есть , называют вариацией функционала  и обозначают через  . То есть, в рассматриваемых обозначениях = .Вариационное исчисление можно рассматривать как обобщение раздела дифференциального исчисления, занимающегося отысканием экстремальных значений функций многихпеременных, при этом в вариационном исчислении приращение (или вариация) δy функции  является аналогом приращения  переменной  в дифференциальном исчислении, а вариация δJ функционала J(y) – соответственно аналогом дифференциала df(x) функцииf (x).Если функционал J(y) определён на множестве n раз дифференцируемых функций, то вариация (приращение) аргумента y представляет собой функцию, которую можно дифференцировать n раз, при этом справедливы равенства:   …  то есть производные вариации функции y равны вариациям производных, и если функция y получает приращение , то её k-я производная (k=1… n) получает приращение  В вариационном исчислении рассматривают функционалы вида  где  – непрерывная функция, имеющая на отрезке [a,b] по всем переменным непрерывные частные производные до второго порядка включительно, при этом приращение функционала определяется как Будем в дальнейшем использовать следующие обозначения:  ,  и т.п.Теорема (о вариации функционала). Вариация определённого в пространстве С(1) [a,b] функционала где – непрерывная функция, имеющая по всем переменным непрерывные частные производные до второго порядка включительно, определяется формулой = Доказательство. Если – вариация (приращение) функции y(x), то (с учётом того, что производные вариации n раз дифференцируемой функции равны вариациям производных)  = . Применяя к приращению  , записанному, как и ранее (непосредственно перед теоремой), в виде разности подынтегральных функций, формулу Тейлора (в форме записи для функции двух переменных), с использованием переобозначений  и т.д.,получаем следующее соотношение  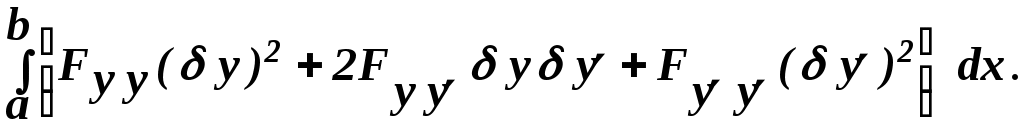=    .Из определения нормы δy для пространства С(1) (║δy║  + ) следует, что ≤ ║δy║ и  ≤ ║δy║ .По условию теоремы вторые частные производные непрерывны, поэтому в соответствии с теоремой Вейерштрасса, они ограничены, то есть существует постоянная М>0, такая, что │  │,│ │,│ │≤ M. |