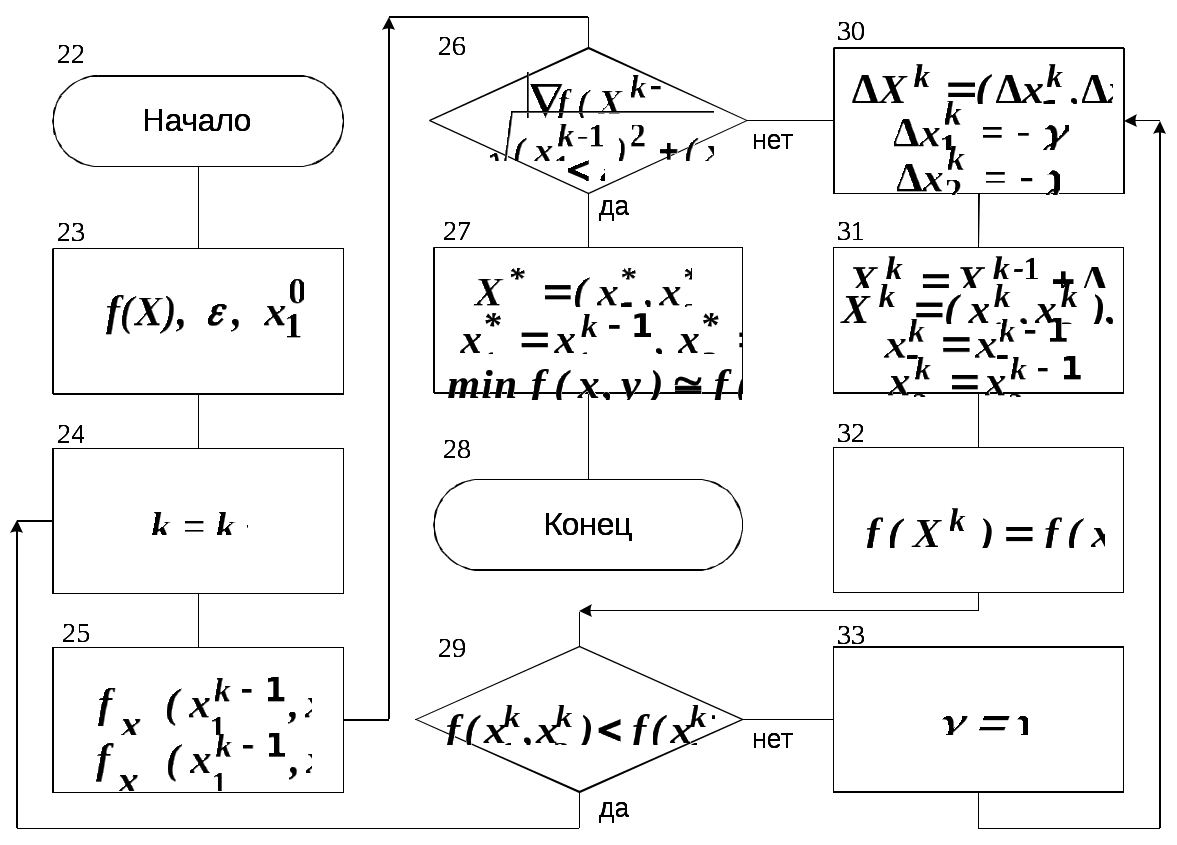Теория оптимизаций. ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций. Общие сведения о теории оптимизации

• Название: Общие сведения о теории оптимизации
• Анкор: Теория оптимизаций
• Дата: 25.01.2022
• Размер: 2.93 Mb.
• Имя файла: ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций.doc
• Тип: Лекция; #342116
• страница: 10 из 10

26) Геометрическая интерпретация градиентных методов Запись градиента и процедуры поиска экстремума градиентным методом в матричной форме

27) Градиент функции n переменных с пояснениями в аналитической форме

28) Метод градиентного спуска, схема алгоритма

29) Метод градиентного спуска с постоянным шагом

Лекция 8. Модификации градиентных методов
8.1 Классификация методов

Модифицированные градиентные методы представляют собой усовершенствованные простейшие методы, дополненные процедурами, обеспечивающими упрощение вычислительных процедур и сокращение количества шагов итерационного процесса, требуемых для поиска экстремума.

Градиентные методы можно классифицировать по различным признакам.

По количеству n варьируемых переменных в функции, для которой осуществляется поиск экстремума, среди градиентных методов выделяют:

одномерные (n=1),

многомерные (n>1).

По присутствию ограничений градиентные методы делят на:

без ограничений (безусловная оптимизация),

с ограничениями (условная оптимизация).

По типу информации, используемой при поиске экстремума, методы делят на:

градиентные методы первого порядка, в которых при поиске экстремума функции используются значения её первых производных;

градиентные методы второго порядка, в которых при поиске экстремума функции наряду с первыми производными используются и вторые производные.

Ни один градиентный метод не является универсальным. Все они различаются спецификой используемых математических процедур, и в каждом конкретном случае необходимо выбирать метод, соответствующий конкретным особенностям решаемой задачи.
8.2 Градиентные методы первого порядка
8.2.2 Метод наискорейшего спуска
Метод наискорейшего спуска относят к классу градиентных, хотя при нём градиент определяют только в начальной точке, а затем только при необходимости.

Рис.3 Поиск наименьшего значения функции методом наискорейшего спуска

На рис. 3 показана траектория поиска наименьшего значения целевой функции по методу наискорейшего спуска. Движение в найденном направлении осуществляется с постоянным шагом до тех пор, пока уменьшается значе­ние рассматриваемой функции , подсчёт которой обычно представляет более простую операцию, чем подсчёт градиента.

Если на каком-то шаге значение не уменьшилось, а возросло (условие приближения к минимуму нарушено), то выполняемое с постоянным шагом движение в данном направлении прекращают, приращение последнего шага снимают наполовину и вычисляют новый градиент функции , определяющий направление дальнейшего движения с новой величиной постоянного шага.

Схема алгоритма метода наискорейшего спуска представлена на рис. 4.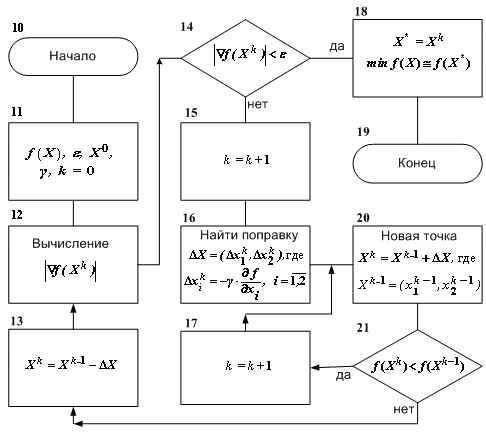

Рис. 4. Алгоритм метода

наискорейшего градиентного спуска

Преимущество метода наискорейшего спуска состоит в его простоте, так как в большинстве шагов вычисляются только значения функции , а не вектор-градиент. Но для того, чтобы существенно приблизиться к точке экстремума, шаги не должны быть большими. Поэтому этот метод также предполагает значительное количество шагов.

Для закрепления изложенных теоретических положений рассмотрим задачу в следующей математической постановке: «Найти минимум функции
f( )=( )²+15 +( )²+11 +
при заданных исходных данных о координатах начальной точки поиска =0и =0, значении, определяющем величину шага γ=1 и точности вычислений ε=0,1».

Фрагмент решения задачи c использованием алгоритма метода наискорейшего градиентного спуска:

1) Исходные данные (блочный символ 11)
k=0; = , = ;γ=1; ε=0,1
2) Вычисление длины вектора-градиента (блочный символ 12)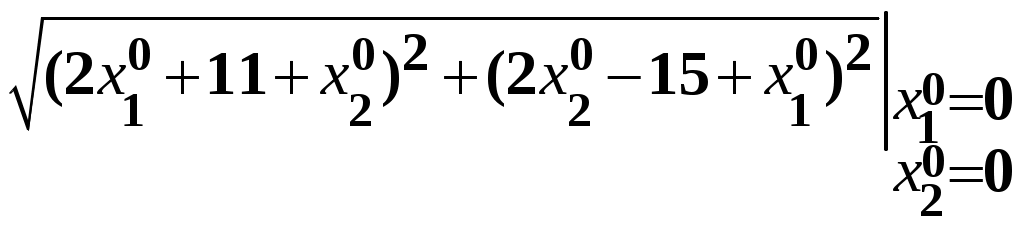

=

= = 18,601.
3) Проверка достижения заданной точности вычислений (блочный символ 14)
=18,601 > ε = 0,1 (не достигнута)
4) Очередной шаг выполнения итерационной процедуры (блочный символ 15) k=k +1=1

5) Нахождение поправки (блочный символ 16)
:

,

.
6) Нахождение координат новой точки (блочный символ 20)
Так как и , то

7) Проверка (блочный символ 21) сохранения условия приближения к минимуму:
,

1.97,
следовательно условие выполнено.

Перейти к предписанию блочного символа 17.

и т. д.
8.2.2 Метод градиентного спуска

с дроблением шага
Схема алгоритма метода градиентного спуска с дроблением шага для частного случая функции двух переменных представлена на рис. 5.


Рис.5. Алгоритм метода

градиентного спуска с дроблением шага
При данном методе сначала определяются (см. блочный символ 25) производные и в начальной точке (при k=1), затем вычисляется (блочный символ 26) величина градиента и осуществляется переход к итерационной процедуре.

В каждом шаге итерационной процедуры:

вычисляется значение 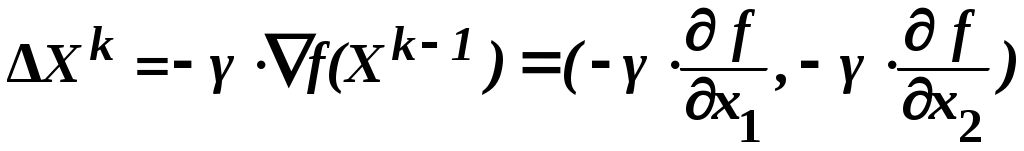поправки (блочный символ 30), причём

;

реализуется (блочный символ 31) итерационное соотношение с использованием поправки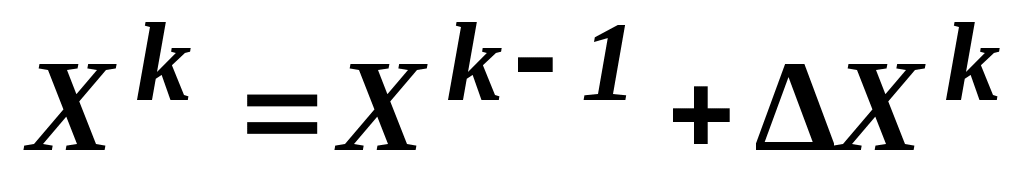
;
определяется (блочный символ 32) значение функции в новой точке;

проверяется (блочный символ 29) сохранение условия монотонности (приближения к минимуму):

Если условие монотонности соблюдается, делается, как и в методе градиентного спуска, следующий шаг поиска экстремума (см. переход от блочного символа 29 к блочному символу 24) с вычислением (блочный символ 25) значений производных, определением (блочный символ 26) нового значения градиента и проверкой условия завершения поиска. При невыполнении такого условия определяются (блочный символ 30) поправка и (блочный символ 31) координаты новой точки в соответствии с итерационным соотношением.

Если же условие монотонности нарушается, значение шага дробится путём деления на 2 (переход от блочного символа 28 к блочному символу 32), пока монотонность не восстановится, и только после этого осуществляется переход к последующим итерациям.
Вычисления прекращают при выполнении условия │ │ < ε.
8.3 Градиентные методы второго порядка
8.3.1 Метод Ньютона
Этот метод, как и ряд других методов второго порядка, применим лишь тогда, когда рассматриваемая функция является дважды дифференцируемой и строго выпуклой – только тогда обеспечивается сходимость метода (именно при таких

условиях разложение целевой функции в ряд Тейлора в окрестности точки минимума оказывается достаточно точным и при значительном удалении от ).
Поэтому при методе Ньютона в векторе поправок возвращаются от матрицы Г к матрице, обратной матрице A, элементами которой служат частные производные второго порядка заданной функции, вычисленные в произвольной точке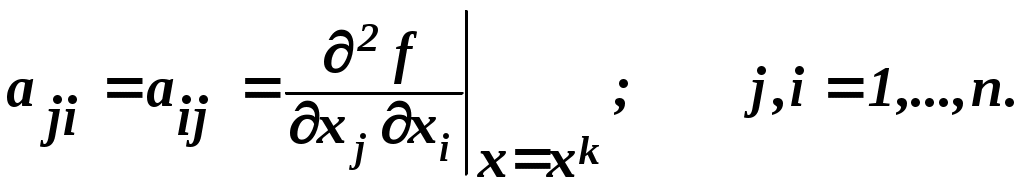



С учётом сказанного, вектор поправок при методе Ньютона имеет вид
.
Если разложение в ряд Тейлора с удержанием только линейных членов достаточно точно представляет рассматриваемую функцию, то точка минимума достигается достаточно быстро, причём теоретически это возможно за один шаг.
Практически достичь требуемого результата за один шаг в большинстве случаев оказывается невозможным, и поэтому выполняют некоторую последовательность итераций с заданным шагом 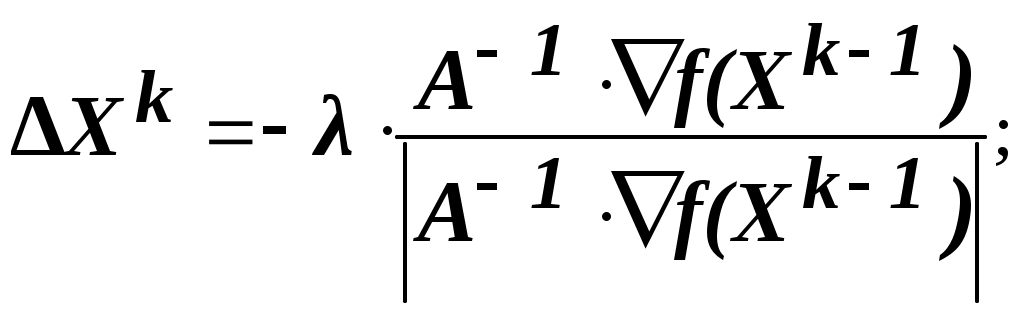в соответствии со следующими соотношениями:



где

– длина вектора .

Вычисления проводят до тех пор, пока не выполнится условие сходимости:

│ │ < ε ,

где – заданная точность.
8.3.2 О других методах второго порядка
Метод Ньютона с учётом специфики некоторых частных случаев оптимизации и выявленных дополнительных возможностей получил своё развитие в виде ряда модификаций.

К числу таких модификаций относятся так называемые квазиньютоновские методы, например, такие как метод Ньютона-Рафсона, метод сопряженных градиентов (Флетчера-Ривса), метод Давидона-Флетчера-Пауэлла (ДФП-метод) и ряд других.

Ввиду весьма ограниченного времени, отводимого на изучение преподаваемой дисциплины, квазиньютоновские методы для желающих и заинтересованных могут послужить объектом самостоятельного изучения.
8.3.3 Учёт ограничений

и многоэкстремальные задачи
При нахождении градиентными методами экстремума рассматриваемой функции в условиях дополнительной системы ограничений могут возникнуть трудности.

Система ограничений по существу определяет некоторую допустимую зону значений переменных и некоторую запретную зону, которая не подчиняется системе ограничений.

Поэтому при движении в направлении градиента (или антиградиента) можно встретиться с запретной зоной. В такой ситуации продолжают поиск не в направлении градиента, а вдоль границы запретной зоны, осуществляя на ней поиск экстремума.

При применении градиентных методов возникают сложности и в случаях многоэкстремальных задач, поскольку все рассмотренные методы относятся к классу методов локального поиска. Так как в таких случаях всё зависит от удачности выбора начальной точки целесообразно провести серию процедур поиска, начиная с разных начальных точек, выбираемых при отсутствии более удачных вариантов случайным образом.

Таким образом, можно найти несколько точек локального экстремума и выбрать из них наилучшую.
Краткое заключение по дисциплине
Следует учесть, что рассматриваемые в рамках изучаемой дисциплины «Теория оптимизации» методы нахождения экстремумов функций нескольких переменных, вариационные методы и методы градиентного поиска представляют собой лишь часть общенаучного арсенала методов оптимизации.
Не изученные методы частично будут охвачены дисциплиной «Основы оптимизации управления», запланированной для изучения в следующем семестре и в какой-то части будут предметом самостоятельного изучения при выполнении курсовых работ по обеим названным дисциплинам.

По материалам данной лекции предусмотрена 4-х часовая лабораторная работа.
ЛИТЕРАТУРА
1. Аттетков А.В., Галкин С.В., В.С. Зарубин. Методы оптимизации: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.

12. ГОСТ 19.002-80. Схемы алгоритмов и программ, правила выполнения.
ВОПРОСЫ ДЛЯ САМОКОТРОЛЯ
30) Классификация градиентных методов

31) Метод наискорейшего спуска

32) Метода градиентного спуска с дроблением шага, схема алгоритма

33) Метод Ньютона

34) Учёт ограничений при поиске экстремума градиентными методами и многоэкстремальные задачи