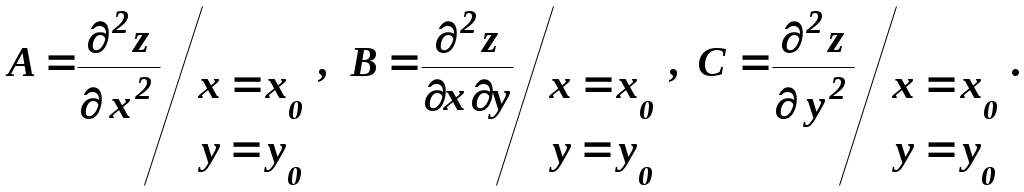Теория оптимизаций. ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций. Общие сведения о теории оптимизации
 Скачать 2.93 Mb. Скачать 2.93 Mb.
|
|
Тема 2. Экстремумы функций нескольких переменных Материалы двух лекций по данной теме в основном представляют собой дословное цитирование § 4 главы VII [4]. Лекция 2.1 Безусловные экстремумы Введение Начнем с рассмотрения функций двух переменных и дадим определение точки экстремума; оно совершенно аналогично соответствующему определению для функций одной переменной. Определение. Точка Р0 (х0 , у0)называется точкой экстремума (максимума или минимума) функции z= f (x, у), если f(x0 , y0)есть соответственно наибольшее или наименьшее значение функции f(x,y)в некоторой окрестности точки Р0 (x0 , y0). При этом значение f (x0 , y0)называется экстремальным значением функции (соответственно максимальным или минимальным) Говорят также, что функция f(x, у) имеет в точке Р0 (х0, у0) экстремум (или достигает в точке Р0 экстремума).
1 Необходимые условия экстремума Начнём с формулирования и доказательства признака экстремума. Необходимый признак экстремума. Если дифференцируемая функция z = f (x,y)в точке Р0(х0,у0 ) имеет экстремум, то ее частные производные в этой точке равны нулю, то есть 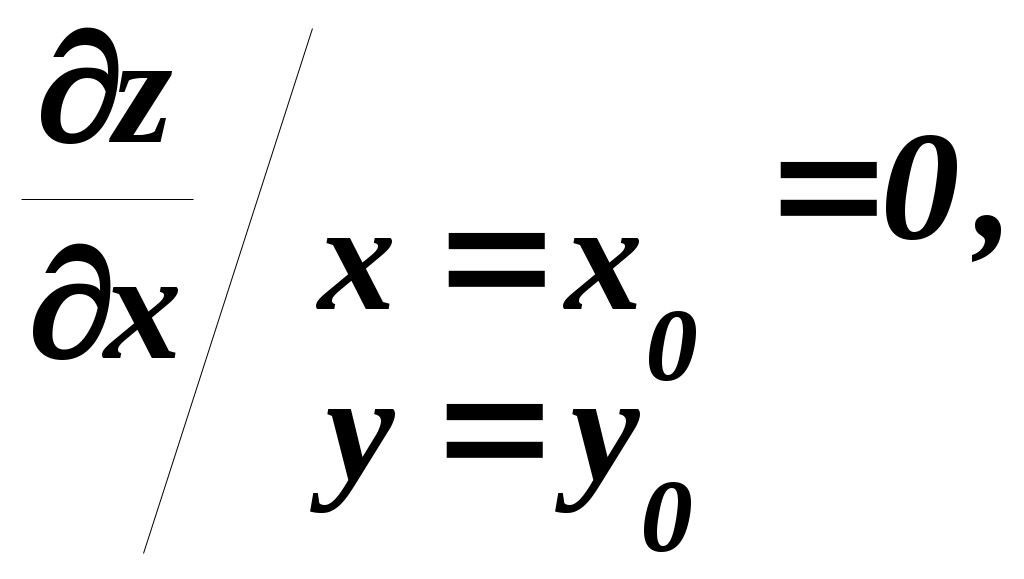 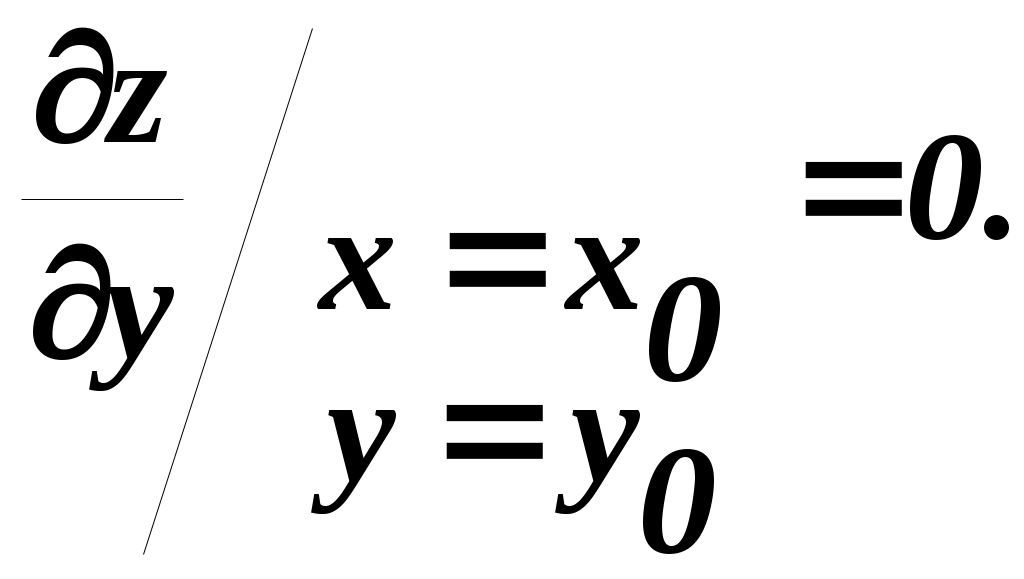 Доказательство. Допустим, что функция z Согласно определению экстремума, функция z 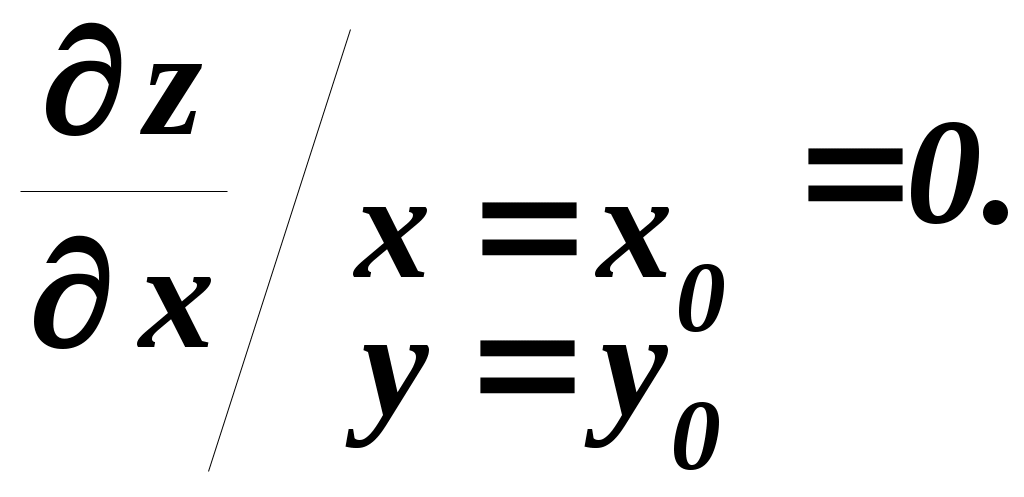 Аналогично функция z 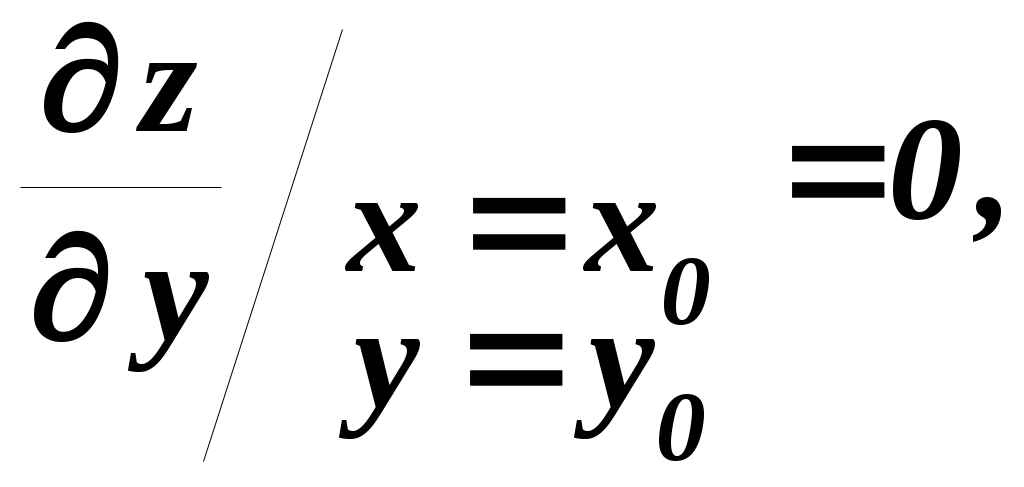 что и требовалось доказать. Точка Р0(х0,у0),координаты которой обращают в нуль обе частные производные функцииz Уравнение касательной плоскости к поверхности z 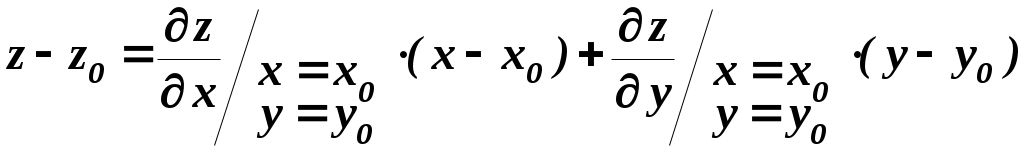 для стационарной точки ввиду равенства частных производных нулю, принимает вид Следовательно, необходимое условие достижения дифференцируемой функцией z Для отыскания стационарных точек функции z 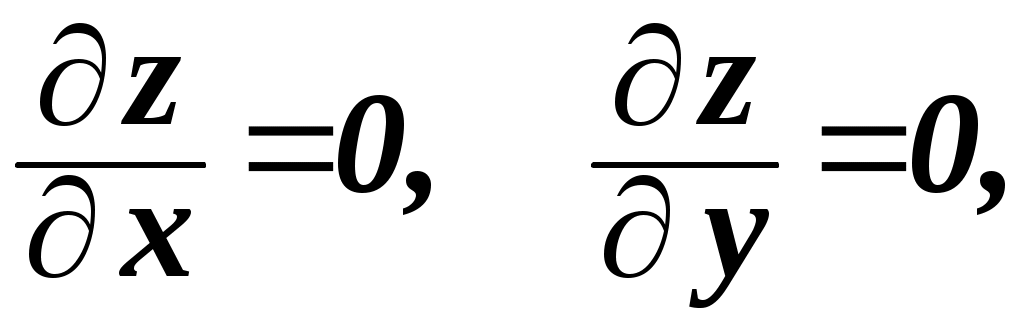 и решить полученную систему двух уравнений с двумя неизвестными. Пример 1. Найдем стационарные точки функции z=2x3+xy2+5x2+y2. Система двух уравнений принимает вид Наряду с Из второго уравнения следует, что или у = 0, или x = –1. Подставляя по очереди эти значения в первое уравнение, найдем четыре стационарные точки: M1 (0, 0), M2 (– Какие из найденных точек действительно являются точками экстремума, мы установим в следующем пункте, где будет приведено достаточное условие экстремума. Два замечания: 1) иногда удается, и не прибегая к достаточным условиям, выяснить характер стационарной точки функции. Так, если из условия задачи непосредственно следует, что рассматриваемая функция имеет где-то максимум или минимум и при этом необходимым признакам экстремума удовлетворяет только одна точка (т. е. одна пара значений х, у), то ясно, что эта точка и будет искомой точкой экстремума функции; 2) заметим также, что точками экстремума непрерывной функции двух переменных могут быть точки, в которых функция недифференцируема (им соответствуют острия поверхности – графика функции). Так, например, функция Следовательно, если иметь в виду не только дифференцируемые, но и вообще непрерывные функции, то нужно сказать, что Точками экстремума могут быть стационарные точки функции и точки, в которых функция недифференщруема. Вполне аналогично определяется понятие экстремума функции любого числа независимых переменных u = f (x, у, z, ..., t) и устанавливаются необходимые условия экстремума: Дифференцируемая функция п переменных может иметь экстремумы только при тех значениях x, у, z, ..., t, при. которых равны нулю все ее п частных производных первого порядка: …, Эти равенства образуют систему пуравнений с пнеизвестными, решение которых приводит к получению координат стационарных точек. 2 Достаточные условия экстремума для функций двух переменных Так же как и для функций одной переменной, необходимый признак экстремума в случае многих переменных не является достаточным. Это значит, что из равенства нулю частных производных в данной точке вовсе не следует, что эта точка обязательно является точкой экстремума. Возьмем функцию z = xy.Её частные производные Достаточные условия экстремума для функций нескольких переменных носят значительно более сложный характер, чем для функций одной переменной. Мы приведем эти условия без доказательства только для функций двух переменных. Пусть Р0 (х0 ,у0)является стационарной точкой функции z = f (x,у),т. е. 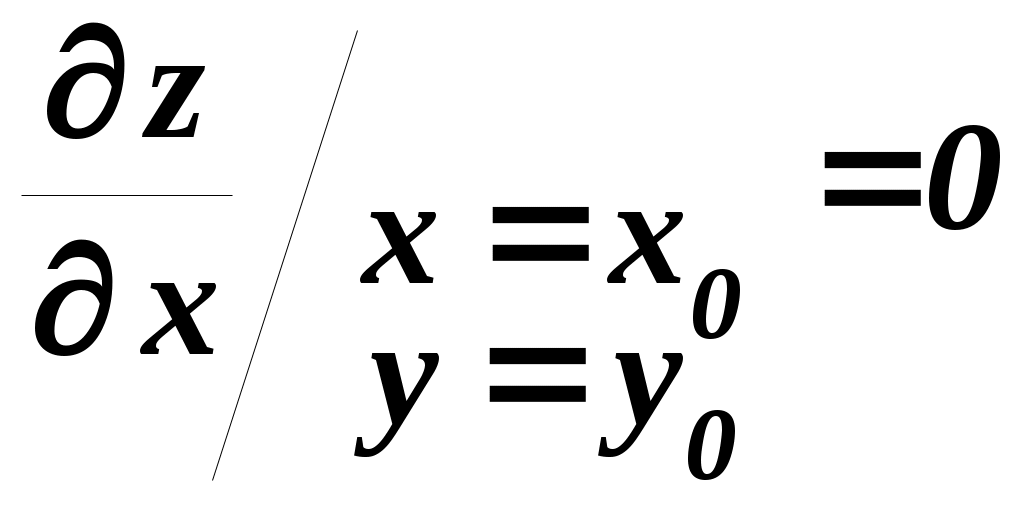 и и 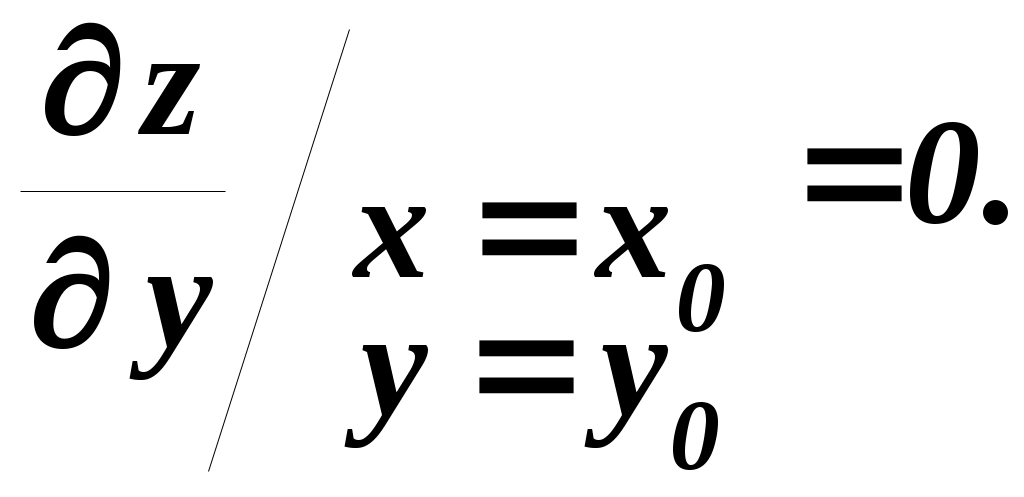 Вычислим в точке Р0 значения вторых частных производных функции f (x, у), обозначив их для краткости буквами А, Ви С:
Правило проверки достаточного условия экстремума: Если B2– АС<0, то функция f (x,y) имеет в точке Р0 (х0 ,у0)экстремум: максимум при А<0 и С<0 и минимум при А>0 и С>0 (из условия В2– АС<0 следует, что А и С обязательно имеют одинаковые знаки, в ином случае приходим к противоречию). Если B2– АС >0, то точка Р0не является точкой экстремума. |