Теория оптимизаций. ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций. Общие сведения о теории оптимизации

• Название: Общие сведения о теории оптимизации
• Анкор: Теория оптимизаций
• Дата: 25.01.2022
• Размер: 2.93 Mb.
• Имя файла: ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций.doc
• Тип: Лекция; #342116
• страница: 8 из 10

С учётом всех неравенств и того, что

│ │ ≤ │ │·│b – a│,

приходим к соотношению

≤ ·4M ║δy║·│b–a│.

Следовательно, второй интеграл в записи формулы Тейлора является бесконечно малой более высокого порядка, чем ║ ║ , и поэтому вариацией функционала является первый интеграл, что и требовалось доказать.

Аналогично доказывается, что в пространстве С⁽¹⁾[a,b] вариация функционала



определяется равенством ,

а также, что в пространстве С⁽ⁿ⁾[a,b] вариация функционала



имеет вид .

Пример 4. Найти для функционала приращение если и .

Искомый результат получим, подставив заданные соотношения для , и в выражение для приращения функционала:



.
2 Экстремум функционала
Говорят, что функционал имеет экстремум, если существует функция , называемая экстремалью, в окрестности которой приращение функционала сохраняет знак; при этом, если , то при имеет максимум, а если , то – минимум.

Теорема (необходимое условие экстремума).

Если функционал имеет экстремум при , то его вариация при (если она существует) обращается в ноль, то есть .

Доказательство. Для определенности предположим, что достигает минимума при . При таком предположении (по определению минимума функционала) в некоторой окрестности ε функции его приращение .

Так как существует вариация функционала, то приращение представимо равенством

(║ ║),

где – главная часть приращения, линейная относительно .

Предположим, что . Поскольку (║ ║) есть бесконечно малая более высокого порядка, чем ║ ║, то она не влияет на знак приращения. Сле­довательно, . Так как в соответствии с предположением, , то (из одинаковости знаков) следует и .
Но из линейности следует, что , то есть (при неодинаковых знаках вариации аргумента y) вариации функционала и имеют разные знаки. Но тогда должен быть сделан вывод, что не сохраняет знака в окрестности функции , и, следовательно, функционал не имеет экстремума при то противоречит условию теоремы.

Полученное противоречие отвергает сделанное предположение, что и доказывает теорему.

Лемма (основная лемма вариационного исчисления).

Пусть – фиксированная непрерывная на [a,b] функция.

Если для любой непрерывной на [a,b] вместе со своей производной функции , такой, что , выполняется равенство

(5)

то на (a,b).

Д оказательство. Предположим, что на (a,b).

Тогда существует точка (a,b), в которой . Пусть для определенности . В этом случае в силу непрерывности существует и интервал , на котором . Рассмотрим функцию



такую, что и непрерывны на [a,b], и при этом .
Так как при функция больше нуля, то (по свойству интеграла) знак сохранится и для интеграла

,

то есть для выбранной функции соотношение (5), указанное в условии леммы, не выполняется. Полученным противоречием лемма доказана.
ЛИТЕРАТУРА
3. Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариационное исчисление и оптимальное управление/Под ред. В.С. Зарубина, А.П. Крищенко. М.: Изд-во МГТУ им. Н.Э. Баумана, 1999.

ВОПРОСЫ ДЛЯ САМОКОТРОЛЯ
14) Вариационное исчисление как раздел математики. Основные понятия: функционал (с примерами), норма и расстояние между функциями в нормированном пространстве. Вычислить расстояние между функциями и в пространстве С[0,2].

15) Основные понятия: вариация аргумента и приращение функционала и его аналитическое представление, соотношения между производными функции и вариациями производных

16) Теорема о вариации функционала (доказательство)

17) Необходимое условие экстремума функционала (доказательство)

18) Основная лемма вариационного исчисления (доказательство воспроизвести самостоятельно)
Лекция 3.2 Уравнение Эйлера
1 Общее решение уравнения Эйлера
Рассмотрим следующую вариационную задачу: в пространстве С⁽¹⁾[a,b] среди всех функций , удовлетворяющих граничным условиям найти такие, которые дают экстремум функционалу



с подынтегральной функцией, непрерывной вместе со своими частными производными до второго порядка включительно.

Рассматриваемая задача относится к классу вариационных задач с закрепленными концами. Необходимые условия решения этой задачи определяет следующая теорема.

Теорема (уравнение Эйлера).

Если функционал имеет экстремум при , причём С¹[a,b] и удовлетворяет граничным условиям то функция является решением уравнения

,

которое называют уравнением Эйлера.
Доказательство.Согласно теореме о вариации функционала,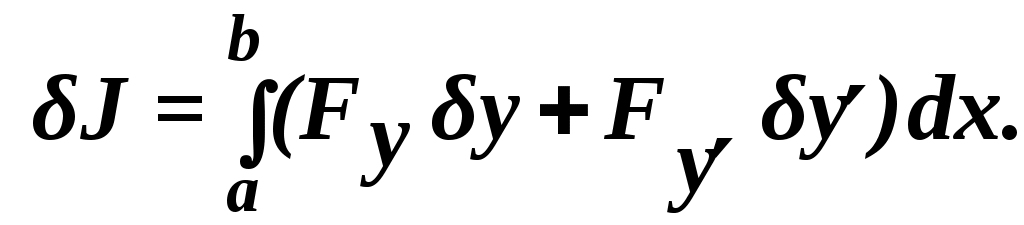



Пусть имеет экстремум при .

По необходимому условию экстремума, вариация функционала должна равняться нулю

Применим к последнему интегралу 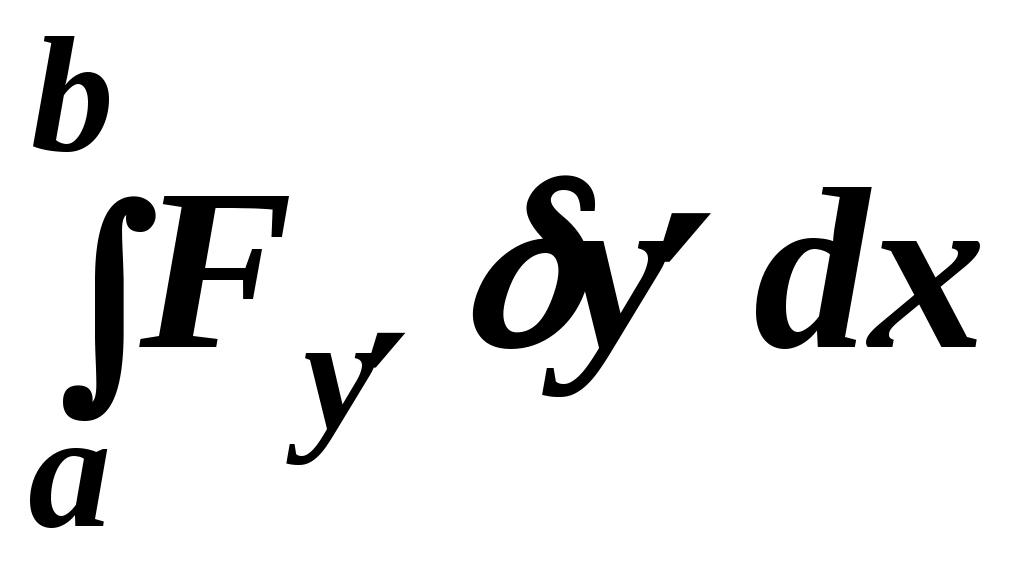формулу интегрирования по частям ( , полагая и , при этом ):

Граничные условия предопределяют, что закреплённые концы функций в точках и варьированию не подлежат, то есть
С учётом этого, , и, следовательно,



Для завершения доказательства перейдём к трактовкам, использованным в формулировке леммы вариационного

исчисления: функция непрерывна на [a,b], а

функция непрерывна вместе со своей первой производной на [a,b] и удовлетворяет условию .
В таком случае, согласно лемме, получается, что



и, следователь­но, функция является решением уравнения Эйлера, что и требовалось доказать.

Функции, являющиеся решениями уравнения Эйлера, представляют собой экстремали.

Уравнение Эйлера играет фундаментальную роль в вариационном исчислении. Оно представляет собой дифференциальное уравнение второго порядка. Общее решение этого уравнения содержит две произвольные постоянные С₁ и С₂ , которые следует определять из граничных условий . В общем случае уравнение Эйлера не разрешимо в квадратурах.

Рассмотренные условия существования экстремума функционала являются лишь необходимыми. Отыскание достаточных условий – довольно сложная задача, поэтому мы ограничимся необходимыми условиями. Но часто сам характер экстремума бывает понятен из каких-то физических соображений, и в таких случаях уравнение Эйлера полностью решет вариационную задачу.
2 Частные случаи уравнения Эйлера
С 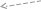лучай1.Функция не содержит явно

В этом случае , и уравнение Эйлера принимает вид из которого следует, что



то есть получаем дифференциальное уравнение первого порядка, не содержащее явно .

Пример 5. Найти экстремаль функционала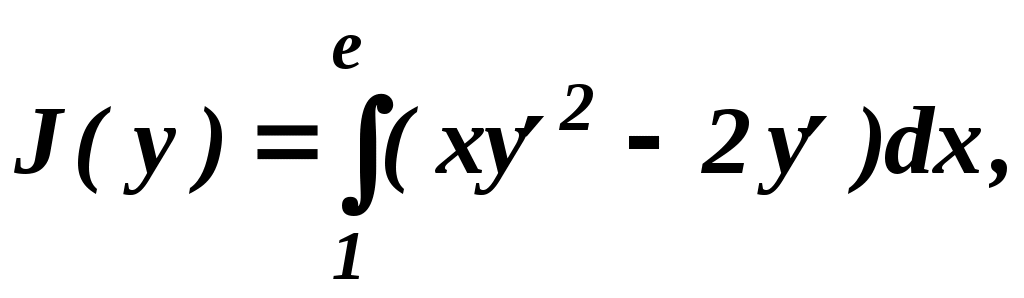

если

Так как подынтегральная функция 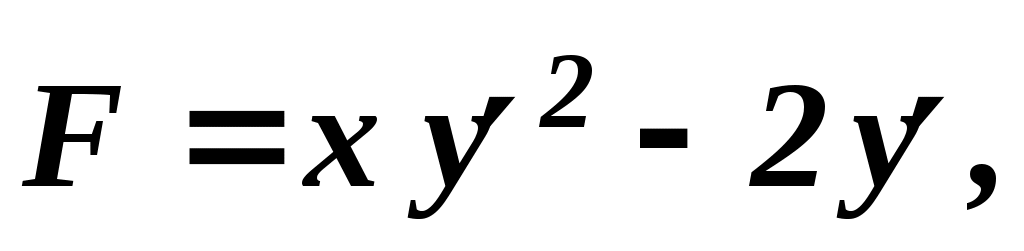не содержит явно , и при этом приходим к уравнению



Найдём общее решение полученного дифференциального уравнения с разделяющимися переменными.



Вычислим значения постоянных используя заданные граничные условия

из = 5 получаем

и из =6 получаем

Подставив найденные значения в общее решение, получаем, что экстремалью заданного функционала является кривая .

Случай 2.Функция не содержит явно

В этом случае .

Преобразуем уравнение Эйлера :

умножим обе его части на при этом получим

,

или (если искусственно ввести члены вида )

. (6)

Так как в соответствии с условиями теоремы не зависит явно от , то первое взятое в скобки выражение

,

а второе выражение, взятое в скобки может быть записано в виде

После соответствующих подстановок соотношение (6) принимает вид



Отсюда следует



Получили дифференциальное уравнение первого порядка, не содержащее явно
Пример 6. Среди всех плоских гладких кривых, соединяющих точки 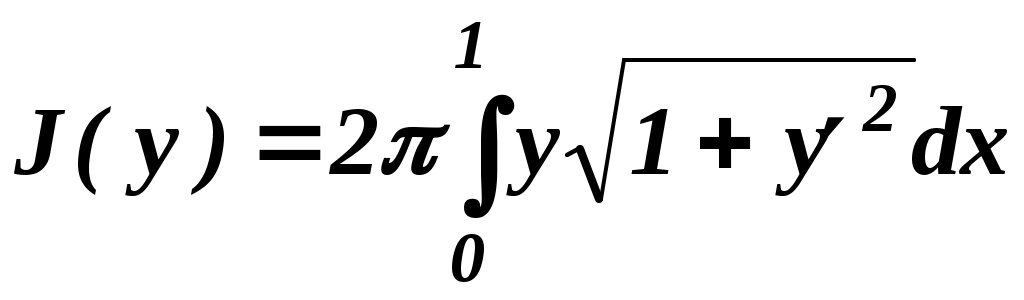и найти ту, которая при вращении вокруг оси образует определяемую функционалом поверхность вращения наименьшей площади.

Так как не зависит от (случай 2), то для нахождения экстремали составим уравнение .

С учётом выражения для 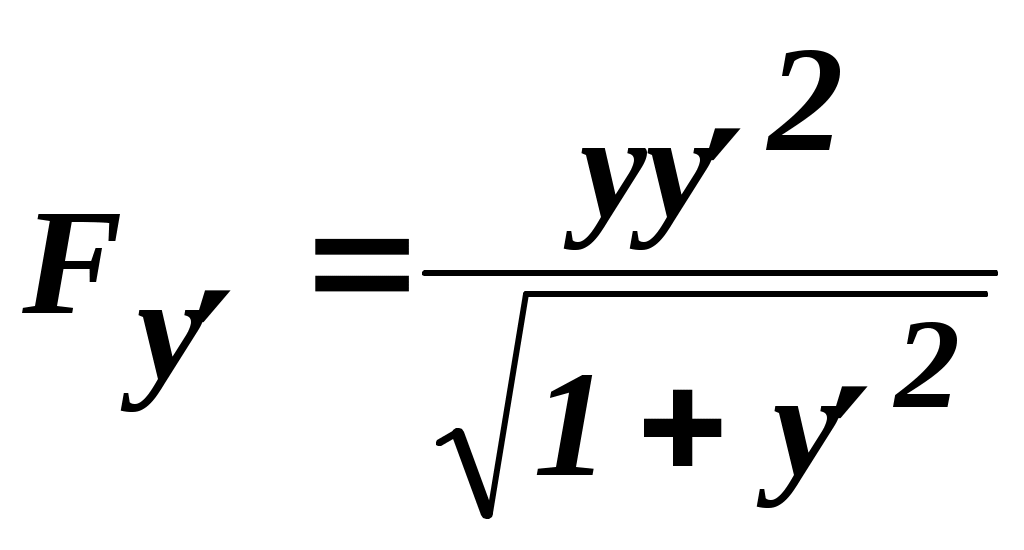, имеем .

Подставив в уравнение выражения для и , получим откуда

Полагая находим при этом (из )

, , ,

с учётом чего получаем общее решение в виде


Найдем . Учитывая, что кривая проходит через точки и при x=0 имеем у(x)=1 и t=– , а при x=1 имеем и t=(1– .
Подставляя эти значения в общее решение, получаем соответственно

.

Отсюда следует С₂ = 0, С₁ = 1.

Итак, экстремалью функционала является цепная линия Среди всех плоских гладких кривых, соединяющих две заданные точки, именно эта линия при вращении вокруг оси образует поверхность наименьшей площади.

Случай3.Функция не содержит явно

В этом случае и уравнение Эйлера , принимающее (ввиду ) вид не является дифференциальным относительно неизвестной функции Если среди кривых, которые определяет это уравнение, есть кривые, удовлетворяющие заданным граничным условиям, то они и будут экстремалями.

Пример 7. Найти экстремаль функционала

если

Ввиду того, что функция

не содержит явно уравнение Эйлера ( ) ввиду принимает вид его

решение , удовлетворяющее заданным граничным условиям, является экстремалью.
Случай4.Функция зависит только от и

В этом случае , и уравнение Эйлера , из которого ввиду того, что , следует соотношение которое, поскольку преобразуется к виду Его общее решение , т. е. экстремалями служат прямые.

Пример 8. Найти экстремаль функционала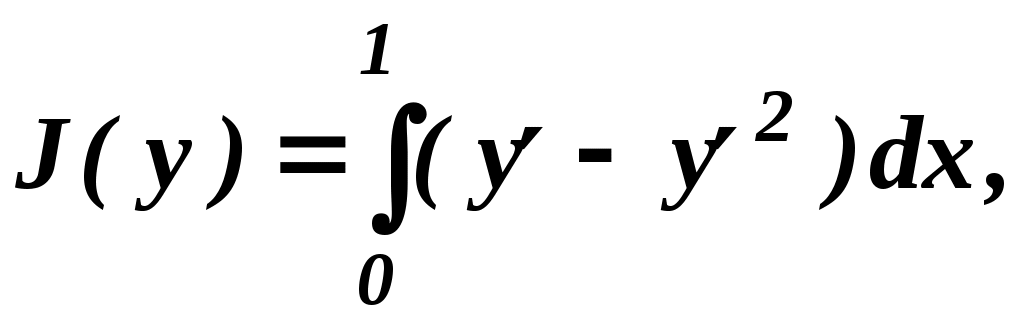

если

Поскольку функция зависит только от , уравнение Эйлера ( ), поскольку и , принимает вид Его общее решение , откуда и .

Найдем и с помощью граничных условий:

при x = 0 значение , а при x = 1

Следовательно, экстремаль – прямая
Случай5. Функция зависит только от .

В этом случае , а уравнение Эйлера приводится к виду .
Пример 9. Найти экстремаль функционала

если
Так как то уравнение Эйлера принимает вид Его решением служит пара прямых но ни одна из них не удовлетворяет заданным граничным условиям, т.к. . Следовательно, данный функционал экстремалей не имеет.

В заключение следует отметить, что могут быть рассмотрены и некоторые другие частные случаи уравнения эйлера, однако в условиях ограниченности выделяемого учебного времени, позвольте выразить уверенность, что подготовка, полученная при изучении преподаваемой дисциплины, а также при изучении высшей математики, вполне позволит Вам при необходимости освоить соответствующие материалы самостоятельно.

3 Функционалы, зависящие от нескольких функций
Рассмотрим простейший случай, когда функционал зависит от двух функций.

Пусть функционал определён в пространстве С⁽¹⁾[a,b], то есть С⁽¹⁾[a,b].

Необходимо найти функции , удовлетворяющие граничным условиям




при которых заданный функционал имеет экстремум.

Функции-экстремали являются решениями системы дифференциальных уравнений, которую называют системой уравнений эйлера:


Система уравнений эйлера в рассматриваемой вариационной задаче играет ту же роль, что и уравнение эйлера в предыдущих задачах.
Для функционала, зависящего от n≥3 функций



Система уравнений эйлера состоит из n уравнений.
По материалам темы «Основы вариационного исчисления» предусмотрена 4 часовая лабораторная работа: «Элементарная задача вариационного исчисления»

ВНИМАНИЕ: Для выполнения лабораторной работы:

1) требуется микрокалькулятор, вычисляющий е^x;

2) при выполнении работы потребуется вычисление полной производной и решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Поэтому целесообразно вспомнить и законспектировать понятие и способ вычисления полной производной (Выгодский М.Я. Справочник по высшей математике, с. 645 – см. выписку в методических документах), а также основные понятия линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами (А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа, с. 582-583) и способ его решения с использованием квадратного уравнения (А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа, с.с. 587-588).
ЛИТЕРАТУРА

3. Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариационное исчисление и оптимальное управление/Под ред. В.С. Зарубина, А.П. Крищенко. М.: Изд-во МГТУ им. Н.Э. Баумана, 1999.

4. А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа. М: Изд-во «Наука», 1967.

ВОПРОСЫ ДЛЯ САМОКОТРОЛЯ
19) Уравнение Эйлера (теорема) с доказательством.

20) Частный случай уравнения Эйлера: когда функция 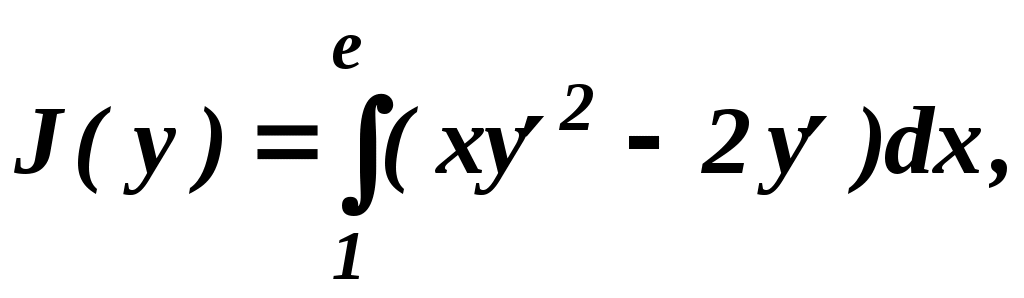не содержит явно . Найти экстремаль функционала если

21) Частный случай уравнения Эйлера: когда функция 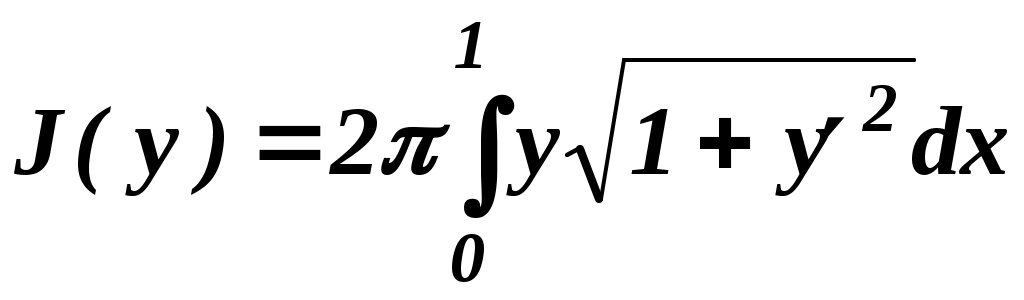не содержит явно . Среди всех плоских гладких кривых, соединяющих точки и найти ту, которая при вращении вокруг оси образует описываемую функционалом поверхность вращения наименьшей площади.

22) Частный случай уравнения Эйлера: когда функция не содержит явно . Найти экстремаль функционала если

23) Частный случай уравнения Эйлера: когда функция зависит только от 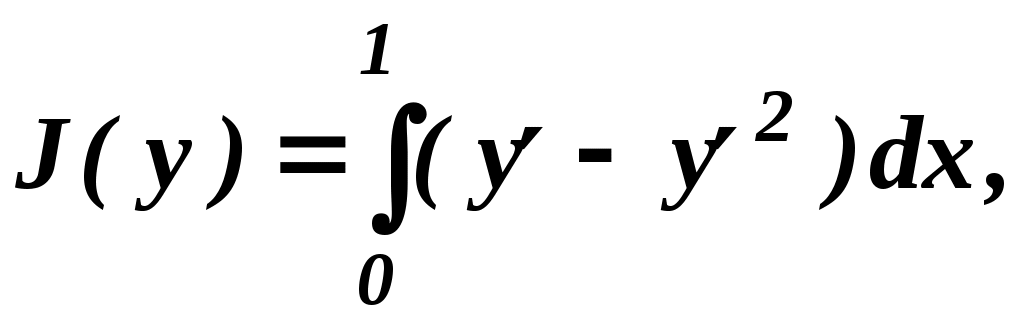при . Найти экстремаль функционала если

24) Частный случай уравнения Эйлера: когда функция зависит только от . Найти экстремаль функционала если

25) Функционалы, зависящие от нескольких функций