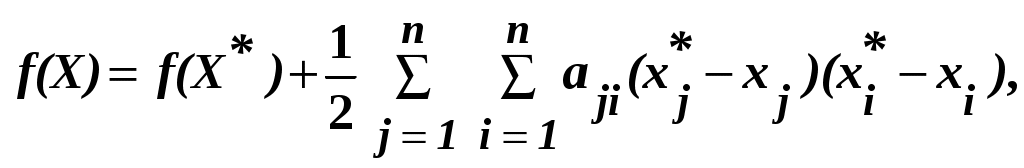Теория оптимизаций. ТЕОРИЯ ОПТИМИЗАЦИИ общий конспект лекций. Общие сведения о теории оптимизации
 Скачать 2.93 Mb. Скачать 2.93 Mb.
|
|
Тема 4 Градиентные методы оптимизации За основу материалов лекций по данной теме взяты рукописные тексты лекций заведующей кафедры математики Ростовского военного института ракетных войск Абаниной Т.И. Лекция 7 Сущность градиентных методов 7.1 Теоретические основы градиентных методов Градиентные методы представляют собой одну из наиболее распространённых групп методов поиска экстремального значения (то есть минимума или максимума) нелинейной функции нескольких переменных и относятся к численным итерационным методам. При таких методах поиск экстремума f(
Рис.1. Геометрическая интерпретация На каждом шаге процедуры поиска минимума движение к точке С геометрической точки зрения каждый такой шаг происходит в направлении, перпендикулярном линиям уровня Как известно, градиентом функции f(X) = f(x1,…, xn) называется вектор, проекциями которого служат значения частных производных этой функции. В  дальнейшем градиент функции f(X) будет обозначаться как дальнейшем градиент функции f(X) будет обозначаться как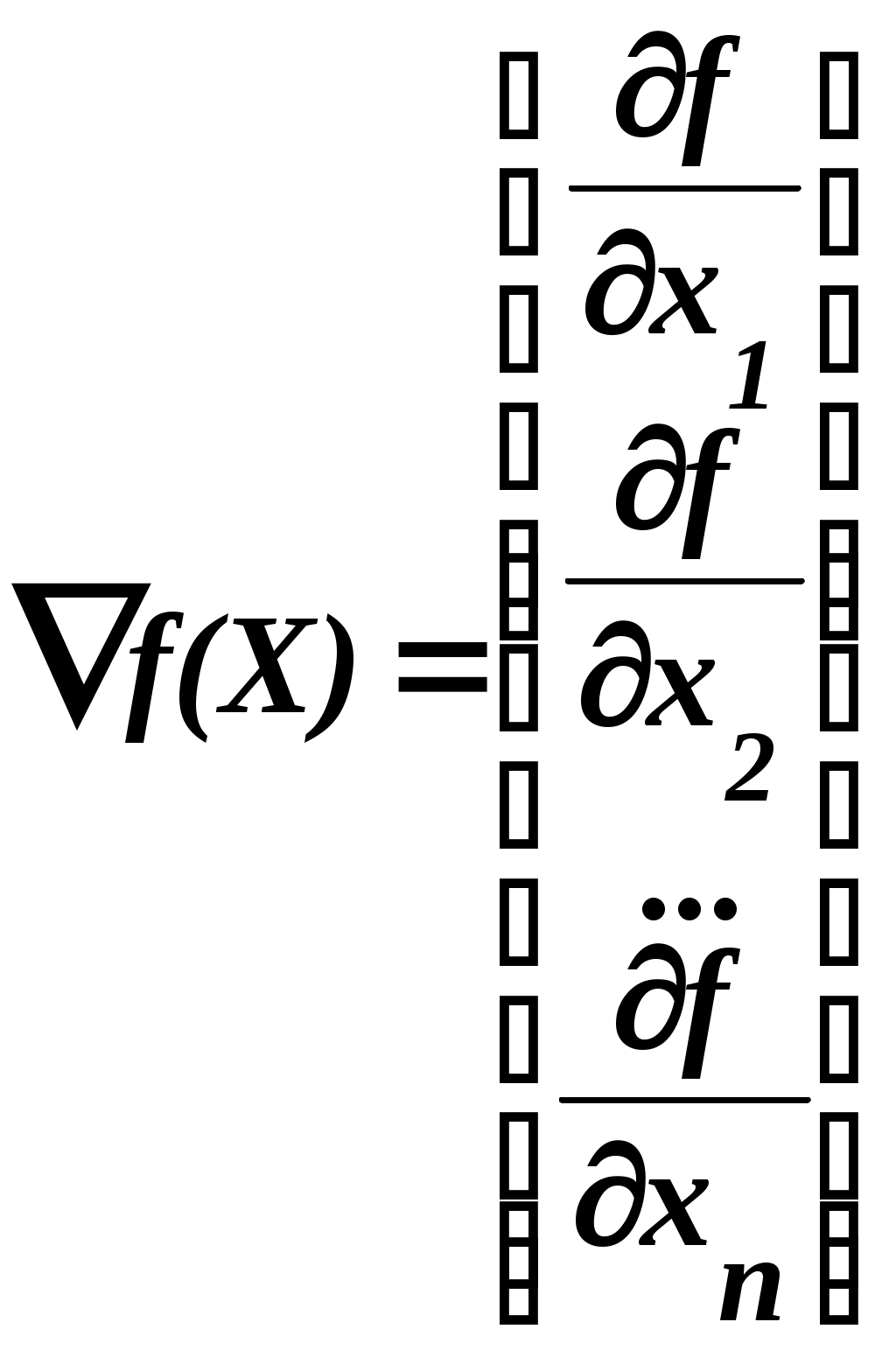 элементы координатами градиента. Градиент  . .Вектор-антиградиент – В силу необходимого условия экстремума в точке экстремума  , , 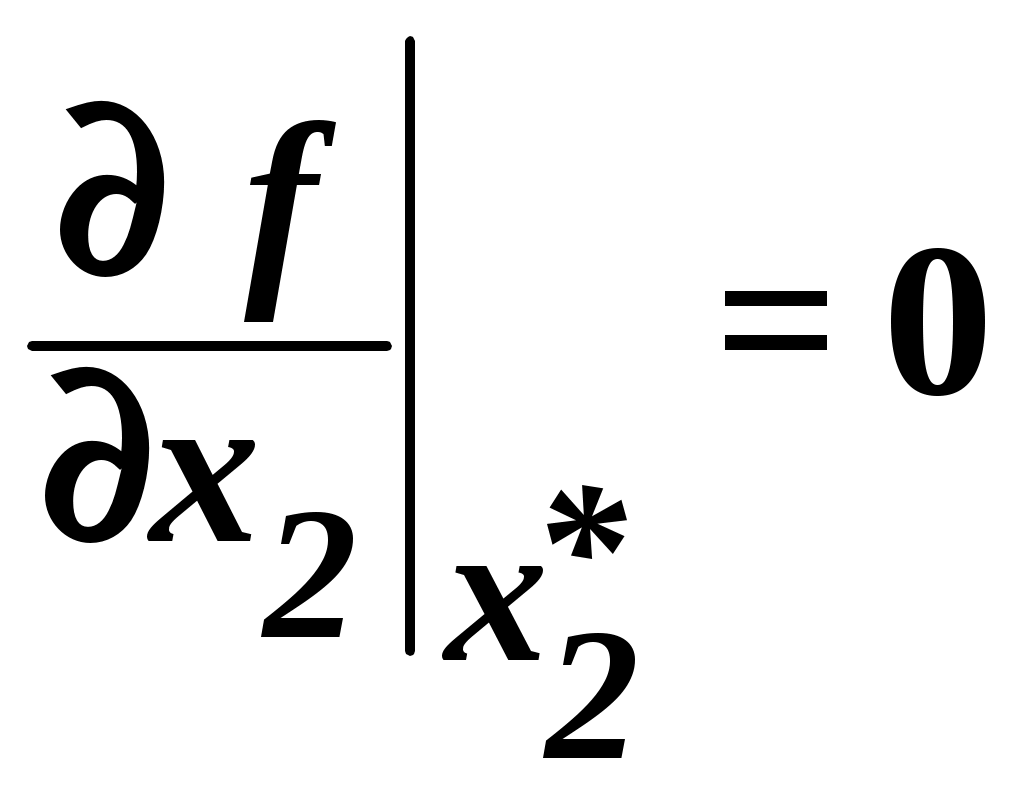 ,…, ,…,  , ,иначе говоря, В дальнейшем будем исходить из предположения, что требуется найти минимум заданной функции. Для рассмотрения сущности градиентных методов поиска экстремума найдём путём разложения в ряд Тейлора с удержанием первых членов ряда до второго порядка включительно квадратичную аппроксимацию функции f(x) в окрестности точки Так как в точке
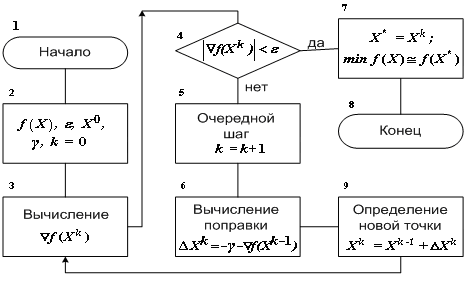
где 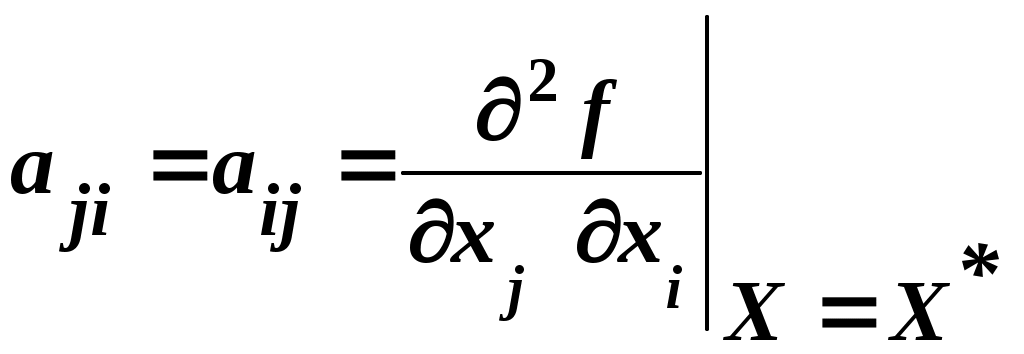 . .Вычислим производные функции f(X) по С учётом того, что 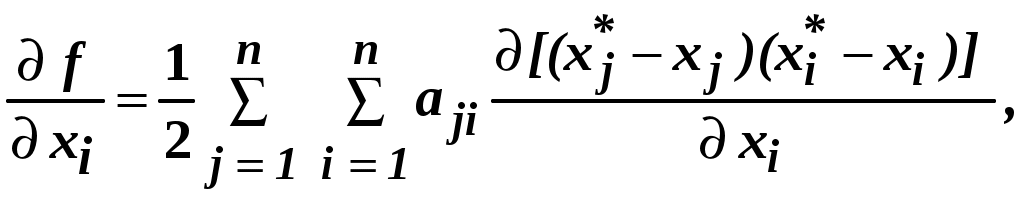 а также того, что в записанном таким образом соотношении содержатся при ( 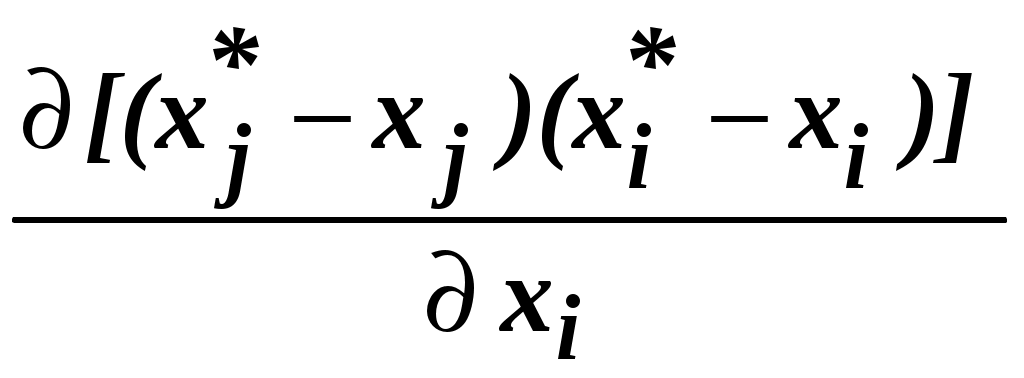 и и  , ,в сумме равных  , также равная , также равная 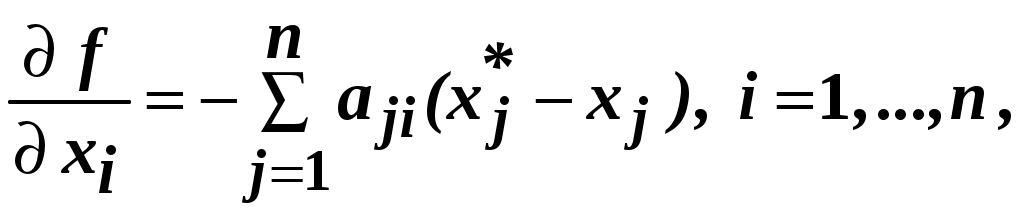 а сам градиент при его записи в матричной форме имеет вид где А – квадратная симметричная матрица размерности Решая записанное в матричной форме уравнение относительно где Если бы разложение функции Поэтому матрицу В матрице Гэлементы Обозначим через  . .Здесь Для того, чтобы последовательность приближений приводила к решению задачи поиска экстремума, элементы матрицы Интегральным условием сходимости, по которому в многошаговой процедуре проверяется достижение оптимума, является Разные способы выбора матриц 7.2 Простейшие градиентные методы 7.2.1 Метод градиентного спуска В методе градиентного спуска, обычно именуемом более просто – градиентным методом (без дополнительных поясняющих слов, характерных для названий других градиентных методов) величины перемещений это означает, что в этом случае матрица  , ,где При методе градиентного спуска на k-м шаге поправка (являющаяся величиной шага) имеет вид а процедура определения новой точки при поиске экстремума записывается как Алгоритм метода градиентного спуска описывается схемой, приведенной на рис. 1.
Рис.2. Алгоритм процедуры поиска минимума функции методом градиентного спуска На рис.1 указана соответствующая ГОСТу [2] нумерация блочных символов, обычно используемая для ссылок на те или иные элементы при пояснении схемы алгоритмов. Особенность метода градиентного спуска состоит в том, что движение к точке экстремума происходит с переменным шагом, поскольку величина приращения шага Так как значение градиента на пологих склонах и вблизи экстремума оказывается слишком малым, то на некоторых участках движения шаги могут оказаться слишком мелкими, что значительно удлиняет время поиска. От этого недостатка попытаться избавиться, если использовать модификацию градиентного спуска с постоянным шагом. 8.2.2 Метод градиентного спуска с постоянным шагом При таком методе величину где Оба рассмотренных простейших метода градиентного спуска имеют следующие недостатки: может быть слишком много шагов; в случаях, когда точка экстремума на каждом шаге необходимо заново определять направление градиента, что требует значительного времени. Кроме того, в случае выбора большой величины шага при методе градиентного спуска с постоянным шагом интегральное условие сходимости, по которому проверяется достижение оптимума ( Вычисление градиента на каждом шаге, позволяющее всё время двигаться в направлении наиболее быстрого убывания целевой функции, замедляет получение окончательного результата. Дело в том, что подсчёт градиента обычно гораздо более сложная операция, чем подсчёт самой функции. Поэтому на практике чаще всего используются различные развития простейших методов и их модификации. ВОПРОСЫ ДЛЯ САМОКОТРОЛЯ |