ответы сессия довгалюк 2 семестр. Определение Правосторонний бинарный поиск
 Скачать 3.01 Mb. Скачать 3.01 Mb.
|
Поиск компонент связностиКомпонентой связности неориентированного графа называется подмножество вершин, достижимых из какой-то заданной вершины. Как следствие неориентированности, все вершины компоненты связности достижимы друг из друга. 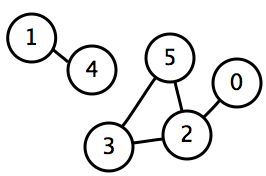 Граф с двумя компонентами связности Граф с двумя компонентами связностиДан неориентированный граф GG с nn вершинами и mm рёбрами. Требуется найти в нём все компоненты связности, то есть разбить вершины графа на несколько групп так, что внутри одной группы можно дойти от одной вершины до любой другой, а между разными группами путей не существует. Для решения задачи модифицируем обход в глубину так, чтобы запустившись от вершины какой-то компоненты, от пометил все вершины этой компоненты — то есть все достижимые вершины — заданным номером этой компоненты. Для этого можно массив used заменить массивом номеров компонент для каждой вершины, изначально заполненный нулями: Теперь проведем серию обходов: сначала запустим обход из первой вершины, и все вершины, которые он при этом обошёл, образуют первую компоненту связности. Затем найдём первую из оставшихся вершин, которые ещё не были посещены, и запустим обход из неё, найдя тем самым вторую компоненту связности. И так далее, пока все вершины не станут помеченными. Записывается это очень компактно: int num = 0; for (int v = 0; v < n; v++) if (!component[v]) dfs(v, num++); После этого переменная num будет хранить число компонент связности, а массив component — номер компоненты для каждой вершины, который, например, можно использовать, чтобы быстро проверять, существует ли путь между заданной парой вершин. Итоговая асимптотика составит O(n + m)O(n+m), потому что такой алгоритм не будет запускаться от одной и той же вершины дважды, и каждое ребро будет просмотрено ровно два раза (с одного конца и с другого). Поиск в ширинуBFS следует концепции «расширяйся, поднимаясь на высоту птичьего полета» («go wide, bird’s eye-view»). Вместо того, чтобы двигаться по определенному пути до конца, BFS предполагает движение вперед по одному соседу за раз. Это означает следующее: 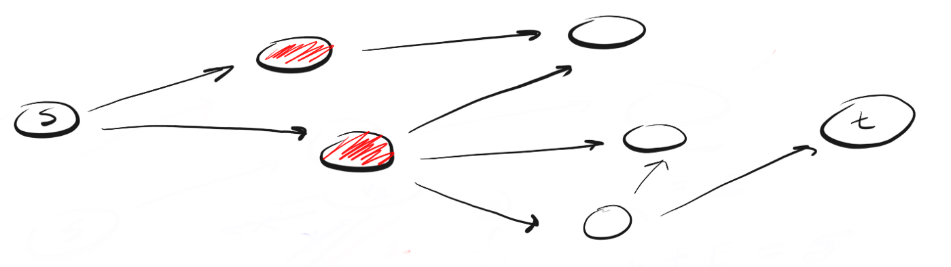 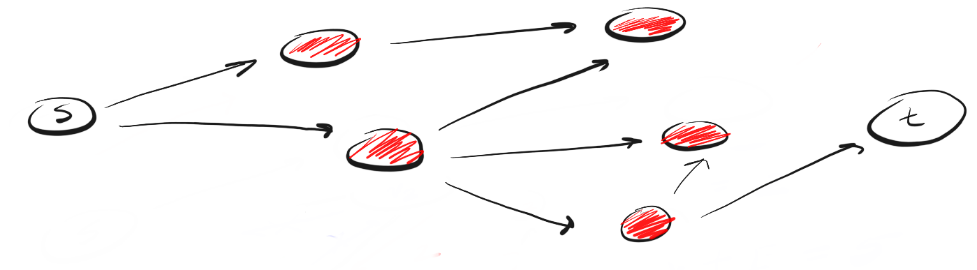 Чем DFS отличается от BFS? Мне нравится думать, что DFS идет напролом, а BFS не торопится, а изучает все в пределах одного шага. Далее возникает вопрос: как узнать, каких соседей следует посетить первыми? Для этого мы можем воспользоваться концепцией «первым вошел, первым вышел» (first-in-first-out, FIFO) из очереди (queue). Мы помещаем в очередь сначала ближайшую к нам вершину, затем ее непосещенных соседей, и продолжаем этот процесс, пока очередь не опустеет или пока мы не найдем искомую вершину. Вот код: Анализ BFSМожет показаться, что BFS работает медленнее. Однако если внимательно присмотреться к визуализациям, можно увидеть, что они имеют одинаковое время выполнения. Очередь предполагает обработку каждой вершины перед достижением пункта назначения. Это означает, что, в худшем случае, BFS исследует все вершины и грани. Несмотря на то, что BFS может казаться медленнее, на самом деле он быстрее, поскольку при работе с большими графами обнаруживается, что DFS тратит много времени на следование по путям, которые в конечном счете оказываются ложными. BFS часто используется для нахождения кратчайшего пути между двумя вершинами. Таким образом, время выполнения BFS также составляет O(V + E), а поскольку мы используем очередь, вмещающую все вершины, его пространственная сложность составляет O(V). DFS использует стек, а BFS — очередь. Время выполнения обоих составляет O(V + E), а пространственная сложность — O(V). Данные алгоритмы имеют разную философию, но одинаково важны для работы с графами. Дейсктры Асимптотика такого алгоритма составит O(n^2)O(n2): на каждой итерации мы находим аргминимум за O(n)O(n) и проводим O(n)O(n) релаксаций. Заметим также, что мы можем делать не nn итераций а чуть меньше. Во-первых, последнюю итерацию можно никогда не делать (оттуда ничего уже не прорелаксируешь). |
