ответы сессия довгалюк 2 семестр. Определение Правосторонний бинарный поиск
 Скачать 3.01 Mb. Скачать 3.01 Mb.
|
Алгоритм Беллмана-ФордаЗадача: В графе могут присутствовать ребра с отрицательными весами. В то же время сложность его равна O(VE), что больше, чем показатель для алгоритма Дейкстры. Алгоритмэтом шаге инициализируются расстояния от исходной вершины до всех остальных вершин, как бесконечные, а расстояние до самого src принимается равным 0. Создается массив dist[] размера |V| со всеми значениями равными бесконечности, за исключением элемента dist[src], где src — исходная вершина. Вторым шагом вычисляются самые короткие расстояния. Следующие шаги нужно выполнять |V|-1 раз, где |V| — число вершин в данном графе. Произведите следующее действие для каждого ребра u-v: Если dist[v] > dist[u] + вес ребра uv, то обновите dist[v] dist [v] = dist [u] + вес ребра uv На этом шаге сообщается, присутствует ли в графе цикл отрицательного веса. Для каждого ребра u-v необходимо выполнить следующее: Если dist[v] > dist[u] + вес ребра uv, то в графе присутствует цикл отрицательного веса. Идея шага 3 заключается в том, что шаг 2 гарантирует кратчайшее расстояние, если граф не содержит цикла отрицательного веса. Если мы снова переберем все ребра и получим более короткий путь для любой из вершин, это будет сигналом присутствия цикла отрицательного веса. ПримерПусть начальная вершина равна 0. Примите все расстояния за бесконечные, кроме расстояния до самой src. Общее число вершин в графе равно 5, поэтому все ребра нужно пройти 4 раза.  Пусть ребра отрабатываются в следующем порядке: (B, E), (D, B), (B, D), (A, B), (A, C), (D, C), (B, C), (E, D). Мы получаем следующие расстояния, когда проход по ребрам был совершен первый раз. Первая строка показывает начальные расстояния, вторая строка показывает расстояния, когда ребра (B, E), (D, B), (B, D) и (A, B) обрабатываются. Третья строка показывает расстояние при обработке (A, C). Четвертая строка показывает, что происходит, когда обрабатываются (D, C), (B, C) и (E, D).  Первая итерация гарантирует, что все самые короткие пути будут не длиннее пути в 1 ребро. Мы получаем следующие расстояния, когда будет совершен второй проход по всем ребрам (в последней строке показаны конечные значения).  Вторая итерация гарантирует, что все кратчайшие пути будут иметь длину не более 2 ребер. Алгоритм проходит по всем ребрам еще 2 раза. Расстояния минимизируются после второй итерации, поэтому третья и четвертая итерации не обновляют значения расстояний.  Примечания: Отрицательные веса встречаются в различных применениях графов. Например, вместо того чтобы увеличивать стоимость пути, мы можем получить выгоду, следуя по определенному пути. Алгоритм Беллмана-Форда работает лучше для распределенных систем (лучше, чем алгоритм Дейкстры). В отличие от Дейкстры, где нам нужно найти минимальное значение всех вершин, в Беллмане-Форде ребра рассматриваются по одному. Алгоритм Флойда-Уоршелла— алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного графа без циклов с отрицательными весами с использованием метода динамического программирования. Находит расстояние от каждой вершины до каждой за количество операций порядка n^3. Веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер (иначе мы можем ходить по нему сколько душе угодно и каждый раз уменьшать сумму, так не интересно). В массиве d[0… n — 1][0… n — 1] на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в качестве «пересадочных» в пути мы будем использовать вершины с номером строго меньше i — 1 (вершины нумеруем с нуля). Пусть идёт i-ая итерация, и мы хотим обновить массив до i + 1-ой. Для этого для каждой пары вершин просто попытаемся взять в качестве пересадочной i — 1-ую вершину, и если это улучшает ответ, то так и оставим. Всего сделаем n + 1 итерацию, после её завершения в качестве «пересадочных» мы сможем использовать любую, и массив d будет являться ответом. n итераций по n итераций по n итераций, итого порядка n^3 операций. Количество вершин в графе, представлением которого является данная матрица, равно 3, и, причем между каждыми двумя вершинами существует ребро. Вот собственно сам этот граф: 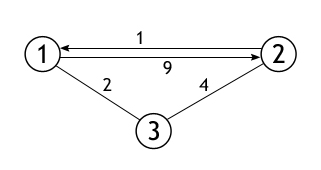 Задача алгоритма: перезаписать данную матрицу так, чтобы каждая ячейка вместо веса ребра из i в j, содержала кратчайший путь из i в j. Для примера взят совсем маленький граф, и поэтому не будет не чего удивительного, если матрица сохранит свое изначальное состояние. Но результат тестирования программы показывает замену двух значений в ней. Следующая схема поможет с анализом этого конкретного примера.  Алгоритм Джонсона: Итак, наша задача – изменить длину каждой дуги таким образом, чтобы избавиться от отрицательных дуг и чтобы все кратчайшие расстояния остались такими же. Как это организовать? Давайте к длине каждой дуги XY добавим h(X) и вычтем h(Y), где h(v) – «чистая» функция, которая определяет некоторое константное значение для каждой вершины. Как рассчитать h? Добавим вершину, связанную со всеми ост вершинами весом 0 Запустим алгоритм Беллмана-Форда для получ графа Результат работы этого алгоритма как раз и даст нам искомые значения функции h для каждой вершины. Суть этих значений – кратчайший путь из вершины S. Поскольку все дуги из S нулевые, то и значения функции h – неположительные. Но пусть это нас не смущает, главное, что полученные значения зафиксированы, не меняются, а, значит, мы можем пересчитать длины всех дуг исходного орграфа: 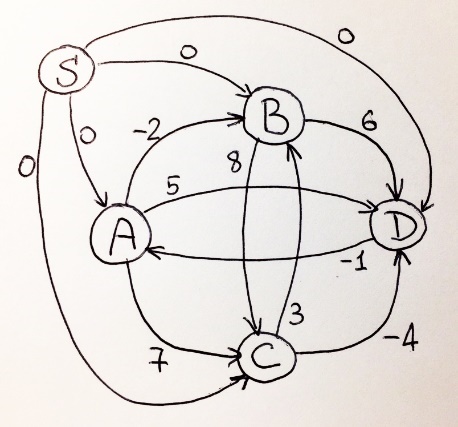 Теперь запустим алгоритм Беллмана-Форда, который найдёт кратчайшие пути от S до всех остальных вершин. Этот алгоритм N раз подряд перебирает все дуги на предмет «релаксации» кратчайших маршрутов из S во все остальные вершины. В таблице перечислены «значимые» итерации работы этого алгоритма, в каждом столбце указана очередная дуга, которая сокращает маршрут до одной из вершин: 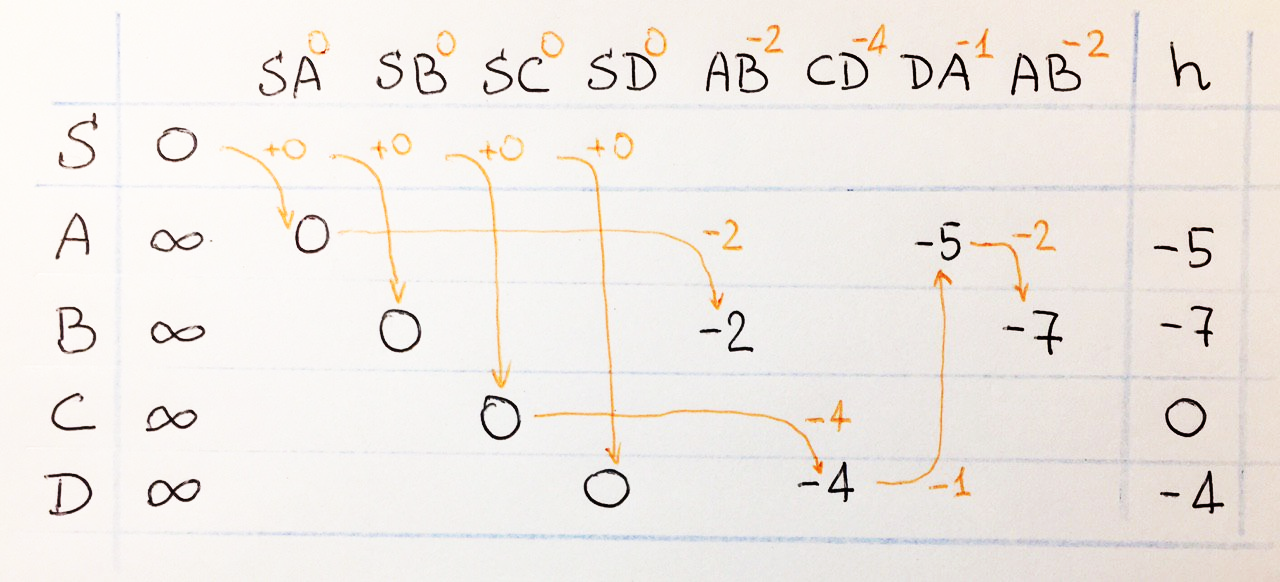 Результат работы этого алгоритма как раз и даст нам искомые значения функции h для каждой вершины. Суть этих значений – кратчайший путь из вершины S. Поскольку все дуги из S нулевые, то и значения функции h – неположительные. Но пусть это нас не смущает, главное, что полученные значения зафиксированы, не меняются, а, значит, мы можем пересчитать длины всех дуг исходного орграфа: 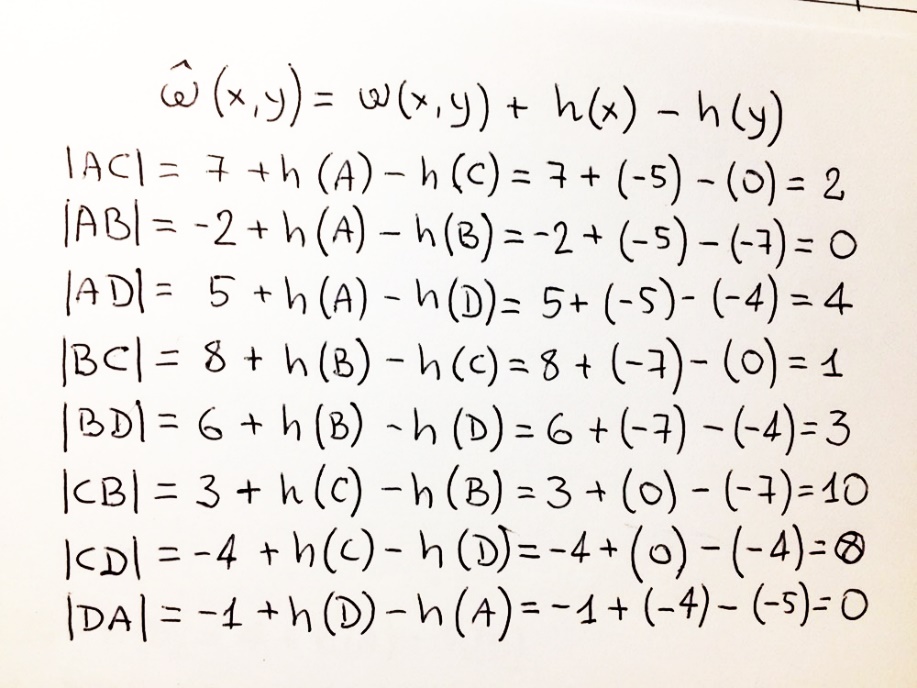 В итоге у нас получится орграф без отрицательных дуг:  Запустим дейкстру для каждой вершины полученного неотрицательного графа |
