ответы сессия довгалюк 2 семестр. Определение Правосторонний бинарный поиск

• Название: Определение Правосторонний бинарный поиск
• Анкор: ответы сессия довгалюк 2 семестр
• Дата: 10.02.2022
• Размер: 3.01 Mb.
• Имя файла: Algoritmy.docx
• Тип: Документы; #357616
• страница: 7 из 11

Понятие АВЛ-дерева

А 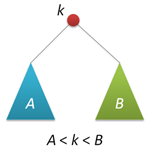ВЛ-дерево — это прежде всего двоичное дерево поиска, ключи которого удовлетворяют стандартному свойству: ключ любого узла дерева не меньше любого ключа в левом поддереве данного узла и не больше любого ключа в правом поддереве этого узла. Это значит, что для поиска нужного ключа в АВЛ-дереве можно использовать стандартный алгоритм. Для простоты дальнейшего изложения будем считать, что все ключи в дереве целочисленны и не повторяются.

Особенностью АВЛ-дерева является то, что оно является сбалансированным в следующем смысле: для любого узла дерева высота его правого поддерева отличается от высоты левого поддерева не более чем на единицу. Доказано, что этого свойства достаточно для того, чтобы высота дерева логарифмически зависела от числа его узлов: высота h АВЛ-дерева с n ключами лежит в диапазоне от log₂(n + 1) до 1.44 log₂(n + 2) − 0.328. А так как основные операции над двоичными деревьями поиска (поиск, вставка и удаление узлов) линейно зависят от его высоты, то получаем гарантированную логарифмическую зависимость времени работы этих алгоритмов от числа ключей, хранимых в дереве. Напомним, что рандомизированные деревья поиска обеспечивают сбалансированность только в вероятностном смысле: вероятность получения сильно несбалансированного дерева при больших n хотя и является пренебрежимо малой, но остается не равной нулю.

Структура узлов

Будем представлять узлы АВЛ-дерева следующей структурой:

struct node // структура для представления узлов дерева

{

int key;

unsigned char height;

node* left;

node* right;

node(int k) { key = k; left = right = 0; height = 1; }

};


Поле key хранит ключ узла, поле height — высоту поддерева с корнем в данном узле, поля left и right — указатели на левое и правое поддеревья. Простой конструктор создает новый узел (высоты 1) с заданным ключом k.

Традиционно, узлы АВЛ-дерева хранят не высоту, а разницу высот правого и левого поддеревьев (так называемый balance factor), которая может принимать только три значения -1, 0 и 1. Однако, заметим, что эта разница все равно хранится в переменной, размер которой равен минимум одному байту (если не придумывать каких-то хитрых схем «эффективной» упаковки таких величин). Вспомним, что высота h < 1.44 log₂(n + 2), это значит, например, что при n=10⁹ (один миллиард ключей, больше 10 гигабайт памяти под хранение узлов) высота дерева не превысит величины h=44, которая с успехом помещается в тот же один байт памяти, что и balance factor. Таким образом, хранение высот с одной стороны не увеличивает объем памяти, отводимой под узлы дерева, а с другой стороны существенно упрощает реализацию некоторых операций.

Определим три вспомогательные функции, связанные с высотой. Первая является оберткой для поля height, она может работать и с нулевыми указателями (с пустыми деревьями):

unsigned char height(node* p)

{

return p?p->height:0;

}


Вторая вычисляет balance factor заданного узла (и работает только с ненулевыми указателями):

int bfactor(node* p)

{

return height(p->right)-height(p->left);

}


Третья функция восстанавливает корректное значение поля height заданного узла (при условии, что значения этого поля в правом и левом дочерних узлах являются корректными):

void fixheight(node* p)

{

unsigned char hl = height(p->left);

unsigned char hr = height(p->right);

p->height = (hl>hr?hl:hr)+1;

}


Заметим, что все три функции являются нерекурсивными, т.е. время их работы есть величина О(1).

Балансировка узлов

В процессе добавления или удаления узлов в АВЛ-дереве возможно возникновение ситуации, когда balance factor некоторых узлов оказывается равными 2 или -2, т.е. возникает расбалансировка поддерева. Для выправления ситуации применяются хорошо нам известные повороты вокруг тех или иных узлов дерева. Напомню, что простой поворот вправо (влево) производит следующую трансформацию дерева: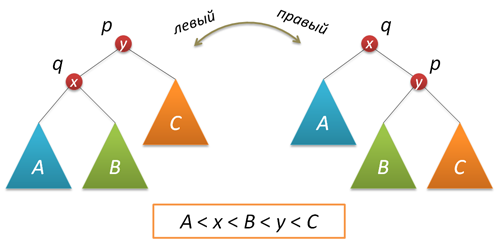



Код, реализующий правый поворот, выглядит следующим образом (как обычно, каждая функция, изменяющая дерево, возвращает новый корень полученного дерева):

node* rotateright(node* p) // правый поворот вокруг p

{

node* q = p->left;

p->left = q->right;

q->right = p;

fixheight(p);

fixheight(q);

return q;

}


Левый поворот является симметричной копией правого:

node* rotateleft(node* q) // левый поворот вокруг q

{

node* p = q->right;

q->right = p->left;

p->left = q;

fixheight(q);

fixheight(p);

return p;

}


Рассмотрим теперь ситуацию дисбаланса, когда высота правого поддерева узла p на 2 больше высоты левого поддерева (обратный случай является симметричным и реализуется аналогично). Пусть q — правый дочерний узел узла p, а s — левый дочерний узел узла q.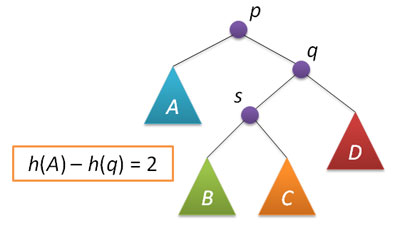



Анализ возможных случаев в рамках данной ситуации показывает, что для исправления расбалансировки в узле p достаточно выполнить либо простой поворот влево вокруг p, либо так называемый большой поворот влево вокруг того же p. Простой поворот выполняется при условии, что высота левого поддерева узла q больше высоты его правого поддерева: h(s)≤h(D).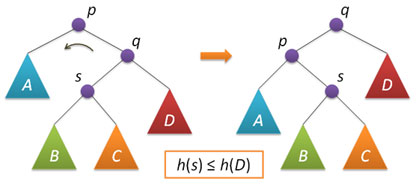



Большой поворот применяется при условии h(s)>h(D) и сводится в данном случае к двум простым — сначала правый поворот вокруг q и затем левый вокруг p.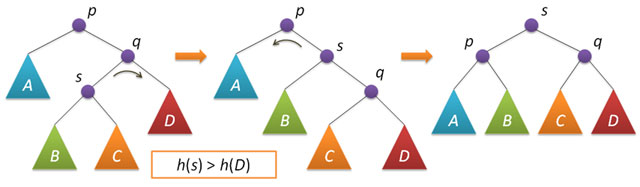



Код, выполняющий балансировку, сводится к проверке условий и выполнению поворотов:

node* balance(node* p) // балансировка узла p

{

fixheight(p);

if( bfactor(p)==2 )

{

if( bfactor(p->right) < 0 )

p->right = rotateright(p->right);

return rotateleft(p);

}

if( bfactor(p)==-2 )

{

if( bfactor(p->left) > 0 )

p->left = rotateleft(p->left);

return rotateright(p);

}

return p; // балансировка не нужна

}


Описанные функции поворотов и балансировки также не содержат ни циклов, ни рекурсии, а значит выполняются за постоянное время, не зависящее от размера АВЛ-дерева.