ответы сессия довгалюк 2 семестр. Определение Правосторонний бинарный поиск

• Название: Определение Правосторонний бинарный поиск
• Анкор: ответы сессия довгалюк 2 семестр
• Дата: 10.02.2022
• Размер: 3.01 Mb.
• Имя файла: Algoritmy.docx
• Тип: Документы; #357616
• страница: 5 из 11

Алгоритм Прима

Суть самого алгоритма Прима тоже сводится к жадному перебору рёбер, но уже из определенного множества. На входе так же имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева.

• 
  Изначально наш подграф состоит из одной любой вершины исходного графа.
  
• 
  Затем из рёбер инцидентных этой вершине, выбирается такое минимальное ребро, которое связала бы две абсолютно разные компоненты связности, одной из которых и является наш подграф. То есть, как только у нас появляется возможность добавить новую вершину в наш подграф, мы тут же включаем ее по минимальмально возможному весу.
  
• 
  Продолжаем выполнять предыдущий шаг до тех пор, пока не найдем искомое MST.
  

Разбор конкретного примера

Выбираем чисто случайно вершину E,далее рассмотрим все ребра исходящие из нее, включаем в наше остовное дерево ребро C <--> E; w = 9, так как данное ребро имеет минимальный вес из всех рёбер инцидентных множеству вершин нашего подграфа. Имеем следующее: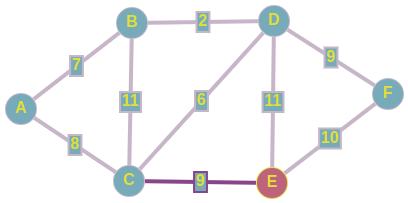

Подграф после добавления 1-го ребра

Теперь выборка производится из рёбер:
D <--> C; w = 6
A <--> C; w = 8
F <--> E; w = 10
B <--> C; w = 11
D <--> E; w = 11

То есть, в данный момент, мы знаем только о двух вершинах, соответственно, знаем о всех ребрах, исходящих из них. Про связи между другими вершинами, которые не включены в наш подграф, мы ничего не знаем, поэтому они на этом шаге не рассматриваются.

Добавляем в наш подграф реброD <--> C и по аналогии добаляем ребро D <--> B. Получаем следующее: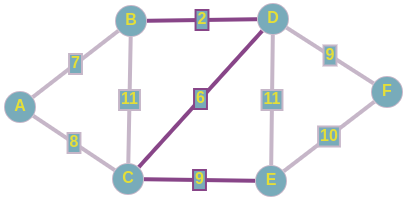

Подграф, полученный после добавления рассмотренных рёбер

Давайте добьем наш подграф до минимального остовного дерева. Вы, наверное, уже догадались о том, по каким ребрам мы будем связывать наши оставшиеся вершины:
A и F.

Проводим последние штрихи и получили тот же самый подграф в качестве минимального остовного дерева. Но как мы раннее говорили, сам подграф ничего не решает, главное тут - множество рёбер, которые включены в наше остовное дерево.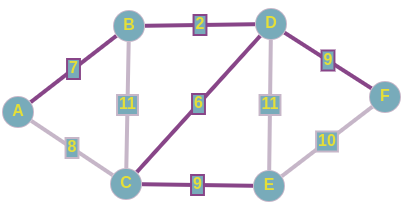

Алгоритм Краскала

Механизм, по которому работает данный алгоритм, очень прост. На входе имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева. Будем рассматривать только связные графы, в другом случае при применении алгоритма Краскала мы будем получать не минимальное остовное дерево, а просто остовной лес.

• 
  Вначале мы производим сортировку рёбер по неубыванию по их весам.
  
• 
  Добавляем i-ое ребро в наш подграф только в том случае, если данное ребро соединяет две разные компоненты связности, одним из которых является наш подграф. То есть, на каждом шаге добавляется минимальное по весу ребро, один конец которого содержится в нашем подграфе, а другой - еще нет.
  
• 
  Алгоритм завершит свою работу после того, как множество вершин нашего подграфа совпадет с множеством вершин исходного графа.
  

Данный алгоритм называется жадным из-за того, что мы на каждом шаге пытаемся найти оптимальный вариант, который приведет к оптимальному решению в целом.

Разбор конкретного примера по шагам

Из представленного сверху графа, выпишем все его ребра в отсортированном порядке:

1) D <--> B; w = 2
2) D <--> C; w = 6
3) A <--> B; w = 7
4) A <--> C; w = 8
5) C <--> E; w = 9
6) D <--> F; w = 9
7) F <--> E; w = 10
8) B <--> C; w = 11
9) D <--> E; w = 11

И начнем по списку добавлять эти ребра в наш остов: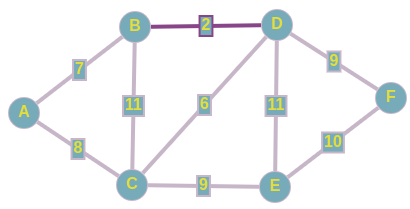

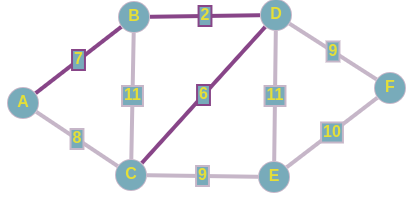Подграф после добавиления 1-го ребра Подграф после добавления 2-го и 3-го рёбер

При добавлении в наше остовное дерево ребра A <--> C, как вы можете заметить, образовывается цикл, поэтому мы просто пропускаем данное ребро.

По итогу у нас образовывается следующий подграф, и как вы заметили, мы соединили все вершины ребрами с минимально-возможными весами, а значит, нашли минимальное остовное дерево для нашего исходного графа.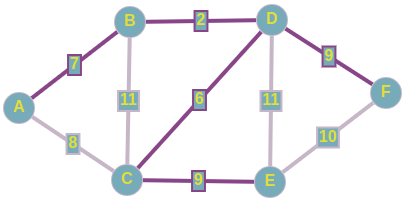

Минимальный остов

Проводим проверку с помощью встроенного алгоритма для нахождения MST на graphonline, и видим, что подграфы идентичны.
И да, из-за того, что при равенстве весов рёбер мы можем выбрать любое из них, конечные подграфы, являющиеся минимальными остовными деревьями, могут различаться с точностью до некоторых рёбер.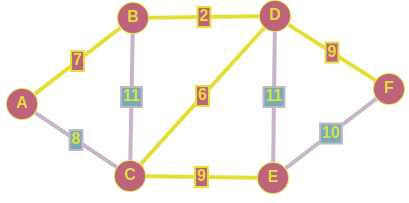

Провели проверку

Суммарный вес искомого MST равен 33.