ответы сессия довгалюк 2 семестр. Определение Правосторонний бинарный поиск
 Скачать 3.01 Mb. Скачать 3.01 Mb.
|
Топологическая сортировкаТопологическая сортировка (Topological sort) — один из основных алгоритмов на графах, который применяется для решения множества более сложных задач. Задача топологической сортировки графа состоит в следующем: указать такой линейный порядок на его вершинах, чтобы любое ребро вело от вершины с меньшим номером к вершине с большим номером. Очевидно, что если в графе есть циклы, то такого порядка не существует. Ориентированной сетью (или просто сетью) называют бесконтурный ориентированный граф. В задачах подобного плана рассматриваются только конечные сети. 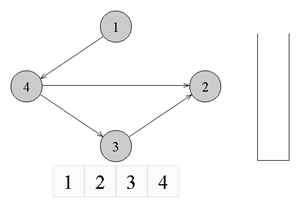 ↑ Пример ориентированного неотсортированного графа, к которому применима топологическая сортировкаИз рисунка видно, что граф не отсортирован, так как ребро из вершины с номером 4 ведет в вершину с меньшим номером (2). Существует несколько способов топологической сортировки — из наиболее известных: Алгоритм Демукрона Метод сортировки для представления графа в виде нескольких уровней Метод топологической сортировки с помощью обхода в глубину Я остановлюсь на рассмотрении последнего, поскольку он наиболее популярен, нагляден и прост в реализации. Суть алгоритмаПоиск в глубину или обход в глубину (англ. Depth-first search, сокращенно DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них. Подробнее о поиске в глубину можно почитать в статье на Хабре. Запускаем обход в глубину, и когда вершина обработана, заносим ее в стек. По окончании обхода в глубину вершины достаются из стека. Новые номера присваиваются в порядке вытаскивания из стека. Цвет: во время обхода в глубину используется 3 цвета. Изначально все вершины белые. Когда вершина обнаружена, красим ее в серый цвет. Когда просмотрен список всех смежных с ней вершин, красим ее в черный цвет. Думаю будет проще рассмотреть данный алгоритм на примере:  ↑ Имеем бесконтурный ориентированный граф. Изначально все вершины белые, а стек пуст. Начнем обход в глубину с вершины номер 1. 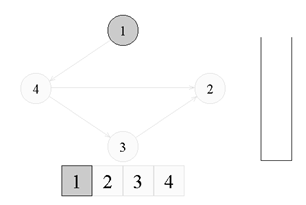 ↑ Переходим к вершине номер 1. Красим ее в серый цвет. 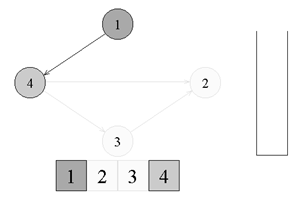 ↑ Существует ребро из вершины номер 1 в вершину номер 4. Переходим к вершине номер 4 и красим ее в серый цвет. 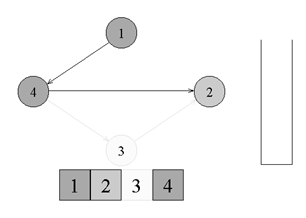 ↑ Существует ребро из вершины номер 4 в вершину номер 2. Переходим к вершине номер 2 и красим ее в серый цвет. 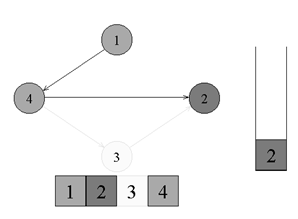 ↑ Из вершины номер 2 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 2 в черный цвет и кладем ее в стек. 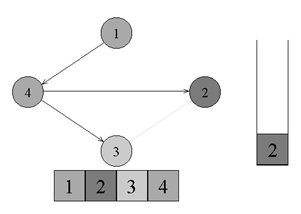 ↑ Существует ребро из вершины номер 4 в вершину номер 3. Переходим к вершине номер 3 и красим ее в серый цвет. 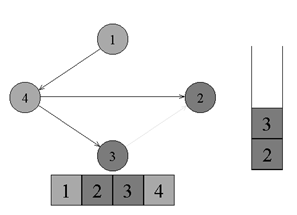 ↑ Из вершины номер 3 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 3 в черный цвет и кладем ее в стек. 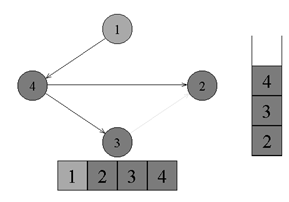 ↑ Из вершины номер 4 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 1. Красим вершину номер 4 в черный цвет и кладем ее в стек. 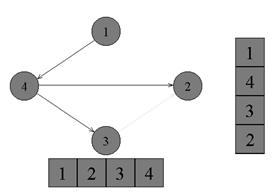 ↑ Из вершины номер 1 нет рёбер, идущих не в черные вершины. Красим её в черный цвет и кладем в стек. Обход точек закончен. 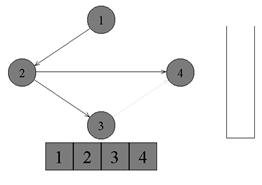 ↑ По очереди достаем все вершины из стека и присваиваем им номера 1, 2, 3, 4 соответсвенно. Алгоритм топологической сортировки завершен. Граф отсортирован. ПрименениеТопологическая сортировка применяется в самых разных ситуациях, например при распараллеливании алгоритмов, когда по некоторому описанию алгоритма нужно составить граф зависимостей его операций и, отсортировав его топологически, определить, какие из операций являются независимыми и могут выполняться параллельно (одновременно). Примером использования топологической сортировки может служить создание карты сайта, где имеет место древовидная система разделов. (если интересно — to google) Сложность по времени: приведенный выше алгоритм это DFS с дополнительным стеком. Таким образом, сложность времени такая же, как и у DFS, которая равна O(V+E). Примечание: также можно использовать вектор вместо стека. Если используется вектор, чтобы получить топологическую сортировку, необходимо выводить элементы в обратном порядке. Применение: Топологическая сортировка в основном используется для составления графика работ из заданных зависимостей между ними. В компьютерных науках применяется для планирования команд, упорядочения ячеек для вычисления формулы при повторном вычислении значений формул в электронных таблицах, логического синтеза, определения порядка задач компиляции для выполнения в make-файлах, сериализации данных и разрешения символьных зависимостей в компоновщиках Поиск сильно связных компонентов Компонентой сильной связности называется класс эквивалентности множества вершин ориентированного графа относительно отношения сильной связности. Другими словами компонента сильной связности = сильно связный подграф. Так как сильная связность — это отношение эквивалентности, то граф разбивается на сильно связные компоненты. Наша задача найти все такие классы эквивалентности. Алгоритм Косарайю Инвертированием ориентированного графа назовем процедуру, в ходе которой поменяем направление каждого ребра на противоположное. Метод Косарайю прост для реализации и понимания. Так как компоненты сильной связности есть циклы, то они совпадают и у исходного графа и у его инвертирования. Пусть дан ориентированный граф G = (V, E). Через G' = (V, E') обозначим интертирование G. Будем обходить граф G в глубину, пока не посетим все вершины. Заведем массив out = [0...|V|-1] — время выхода из вершины. Под временем понимаются логические часы: изначально время равно 0, при переходе в вершину или выходе из неё время увеличивается на 1. 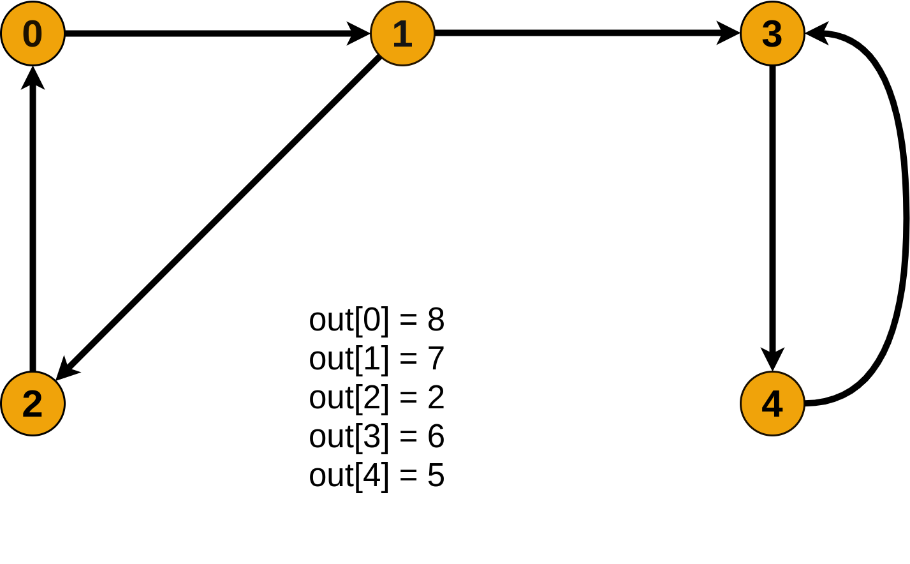 Когда обход закончится, заведем массив vertices, куда добавим все вершины в порядке увеличения времени выхода. Теперь запустим обход в глубинку на инвертированном графе G'. Каждый раз для обхода будем выбирать ещё не посещенную вершину с максимальным индексом в массиве vertices. Все вершины, посещенные в ходе одной итерации dfs, образуют компоненту сильной связности. 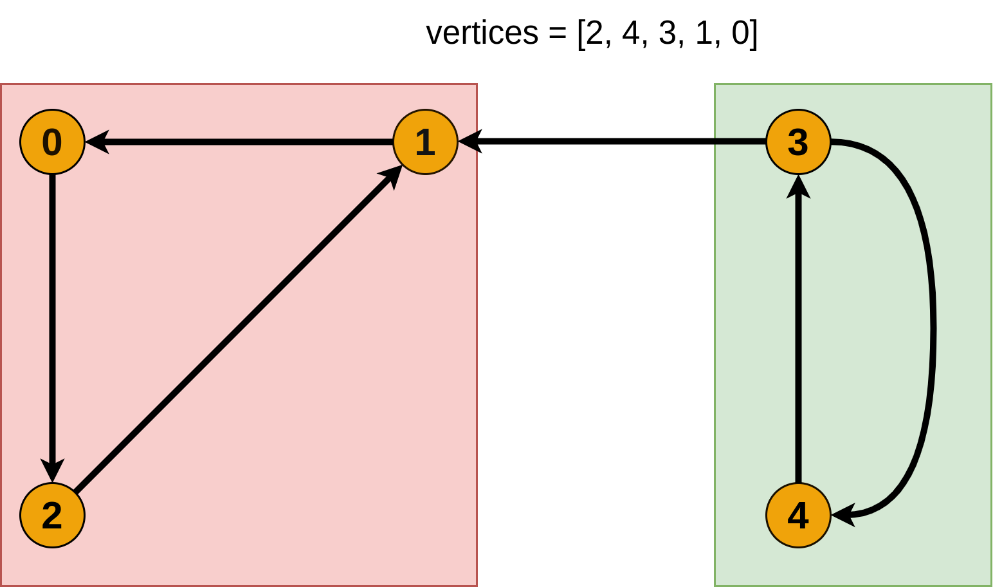 Время работы Заметим: если граф представлен графом смежности, то нам не требуетcя хранить в памяти инвертированный граф. Иначе нам потребуется O(V+E) доп. памяти. Но, в любом случае, нам требуется O(V) памяти для массивов out и vertices. Алгоритм состоит из двух обходов DFS. Каждый работает пропорционально V+E для разреженных графов и V^2 для насыщенных. Кроме того, нам требуется O(VlogV) для сортировки вершин при построении массива vertices. |
