ответы сессия довгалюк 2 семестр. Определение Правосторонний бинарный поиск

• Название: Определение Правосторонний бинарный поиск
• Анкор: ответы сессия довгалюк 2 семестр
• Дата: 10.02.2022
• Размер: 3.01 Mb.
• Имя файла: Algoritmy.docx
• Тип: Документы; #357616
• страница: 10 из 11

Декартово дерево

Следующий пункт нашей обязательной программы — куча (heap). Думаю, также многим известная структура данных, однако краткий обзор я все же приведу.
Представьте себе двоичное дерево с какими-то данными (ключами) в вершинах. И для каждой вершины мы в обязательном порядке требуем следующее: ее ключ строго больше, чем ключи ее непосредственных сыновей. Вот небольшой пример корректной кучи: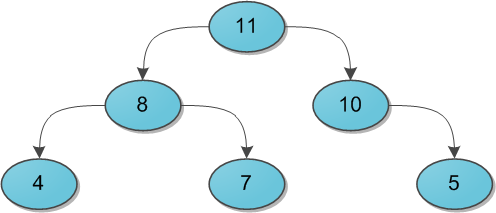


На заметку сразу скажу, что совершенно не обязательно думать про кучу исключительно как структуру, у которой родитель больше, чем его потомки. Никто не запрещает взять противоположный вариант и считать, что родитель меньше потомков — главное, выберите что-то одно для всего дерева. Для нужд этой статьи гораздо удобнее будет использовать вариант со знаком «больше».


Сейчас за кадром остается вопрос, каким образом в кучу можно добавлять и удалять из нее элементы. Во-первых, эти алгоритмы требуют отдельного места на осмотр, а во-вторых, нам они все равно не понадобятся.

Проблемы

Когда речь заходит о деревьях поиска (вы же уже прочитали рекомендуемую статью, правда?), основной вопрос, который ставится перед структурой — скорость выполнения операций, вне зависимости от данных, хранящихся в ней, и последовательности их поступления. Так, двоичное дерево поиска дает гарантию, что поиск конкретного ключа в этом дереве будет выполняться за O(H), где H — высота дерева. Но какой может быть эта высота — черт его знает. При неблагоприятных обстоятельствах высота дерева легко может стать N (количество элементов в нем), и тогда дерево поиска вырождается в обычный список — и зачем оно тогда нужно? Для достижения такой ситуации достаточно добавлять в дерево поиска элементы от 1 до N в очереди возрастания — при стандартном алгоритме добавления в дерево получим следующую картинку: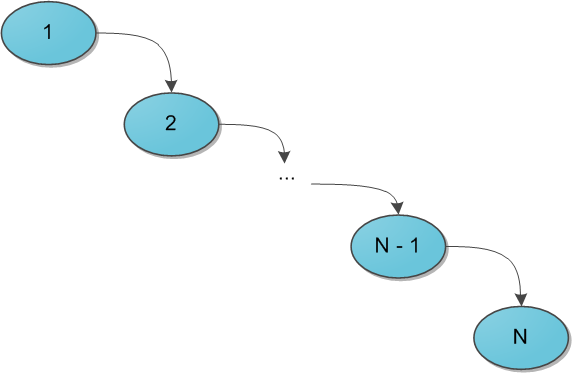

Было придумано огромное количество так называемых сбалансированных деревьев поиска — грубо говоря, тех, в которых по мере существования дерева при каждой операции над ним поддерживается оптимальность максимальной глубины дерева. Оптимальная глубина имеет порядок O(log₂ N) — тогда тот же порядок имеет время выполнения каждого поиска в дереве. Структур данных, поддерживающих такую глубину, много, самые известные тут красно-черное дерево или AВЛ-дерево. Их отличительная черта в большинстве — трудная реализация, основанная на размере чертовой кучи случаев, в которых можно и запутаться. Своей же простотой и красотой выгодно отличается, наоборот, декартово дерево, и даже дает нам в некотором роде то самое желанное логарифмическое время, но лишь с достаточно высокой вероятностью… впрочем, о таких деталях и тонкостях позже.

Определение

Итак у нас есть данные дерева — ключи x (здесь и далее предполагается, что ключ и является той самой информацией, которую мы храним в дереве; когда впоследствии потребуется отделять по смыслу пользовательскую информацию от ключей, я скажу особо). Давайте добавим к ним еще один параметр в пару — y, и назовем его приоритетом. Теперь построим такое волшебное дерево, которое хранит в каждой вершине по два параметра, и при этом по ключам является деревом поиска, а по приоритетам — кучей. Такое дерево и будем далее называть декартовым.

Кстати говоря: в англоязычной литературе очень популярно название treap, которое наглядно показывает суть структуры: tree + heap. В русскоязычной же иногда можно встретить составленные по такому же принципу: дерамида (дерево + пирамида) или дуча (дерево + куча).


Почему дерево называется декартовым? Это сразу станет ясно, как только мы попробуем его нарисовать. Возьмем какой-нибудь набор пар «ключ-приоритет» и расставим на координатной сетке соответствующие точки (x, y). А потом соединим соответствующие вершины линиями, образуя дерево. Таким образом, декартово дерево отлично укладывается на плоскости благодаря своим ограничениям, а два его основных параметра — ключ и приоритет — в некотором смысле, координаты. Результат построения показан на рисунке: слева в стандартной нотации дерева, справа — на декартовой плоскости.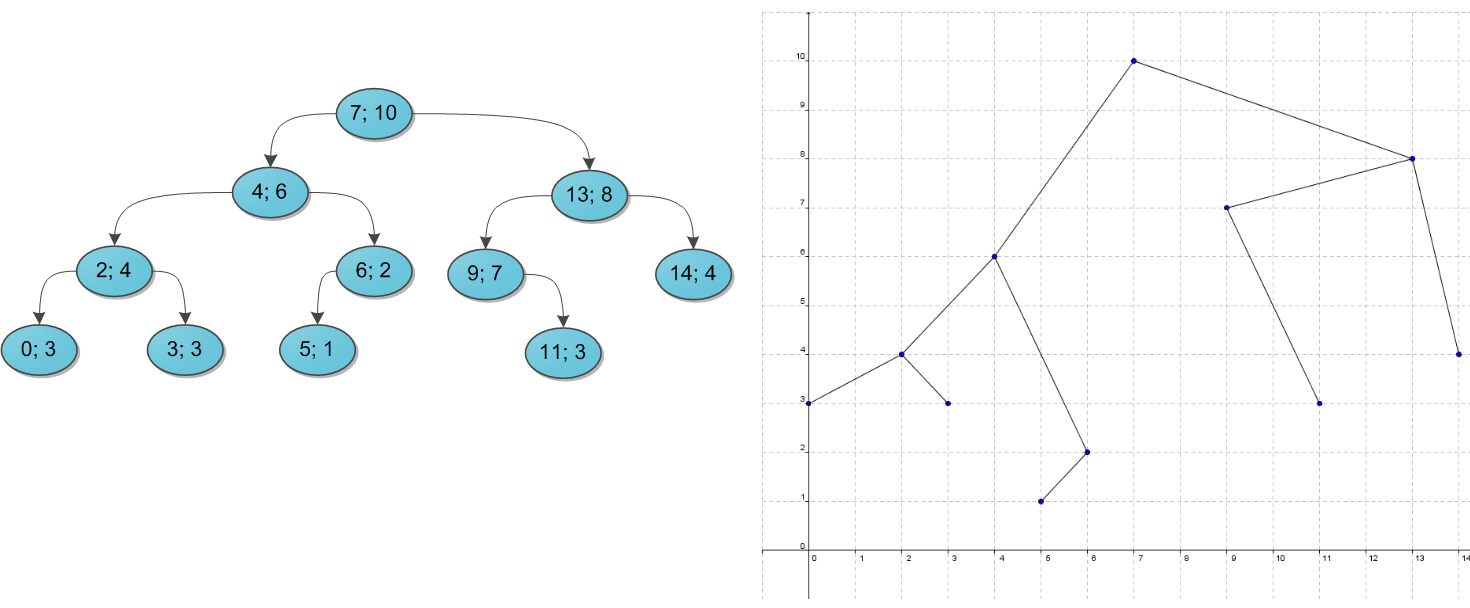


Пока что не очень понятно, зачем такое нужно. А разгадка проста, и кроется она в следующих утверждениях. Во-первых, пусть дано множество ключей: корректных деревьев поиска из них можно построить много различных, в том числе и спископодобное. А вот после добавления к ним приоритетов дерево из данных ключей можно построить уже лишь одно-единственное, вне зависимости от порядка поступления ключей. Это довольно очевидно.
А во-вторых, давайте теперь сделаем наши приоритеты случайными. То есть просто ассоциируем с каждым ключом случайное число из достаточно большого диапазона, и именно оно и будет служить соответствующим игреком. Тогда полученное декартово дерево с очень высокой, стремящейся к 100% вероятностью, будет иметь высоту, не превосходящую 4 log₂ N. (Оставлю этот факт здесь без доказательства.) А значит, хоть оно может и не быть идеально сбалансированным, время поиска ключа в таком дереве все равно будет порядка O(log₂ N), чего мы, собственно, и добивались.

Еще один интересный подход — не делать приоритеты случайными, а вспомнить о том, что у нас есть огромное количество какой-то дополнительной пользовательской информации, которую, как правило, приходится хранить в вершинах дерева. Если есть основания считать, что эта информация по сути своей достаточно случайна (день рождения пользователя, к примеру), то можно попробовать ее использовать в корыстных целях. Взять в качестве приоритета либо непосредственно информацию, либо результат какой-то функции от нее (только тогда функция должна быть обратима, чтобы восстанавливать при необходимости информацию из приоритетов). Впрочем, тут действовать приходится на свой страх и риск — если дерево через какое-то время сильно разбалансируется и вся программа начнет ощутимо тормозить, придется срочно мудрить что-нибудь во спасение ситуации.

Далее для простоты изложения предположим, что все ключи и все приоритеты в деревьях различны. На самом деле возможность равенства ключей не создает никаких особых проблем, вам просто нужно четко определиться, где будут находиться элементы, равные данному x — либо только в левом его поддереве, либо только в правом. Равенство приоритетов по идее тоже не составляет особой проблемы, кроме загрязнения доказательств и рассуждений особыми случаями, но на практике лучше его избегать. Случайная генерация целых приоритетов вполне подходит в большинстве случаев, вещественных между 0 и 1 — почти во всех случаях.


Перед началом рассказа об операциях приведу заготовку класса C#, который будет реализовывать наше декартово дерево.
public class Treap

{

public int x;

public int y;
public Treap Left;

public Treap Right;
private Treap(int x, int y, Treap left = null, Treap right = null)

{

this.x = x;

this.y = y;

this.Left = left;

this.Right = right;

}

// здесь будут операции...

}


Я сделал для простоты изложения x и y типа int, но понятно, что на их месте мог бы быть любой тип, экземпляры которого мы умеем сравнивать между собой — то есть любой, реализующий IComparable или IComparable в терминах C#. В Haskell это мог бы быть любой тип из класса Ord, в F# — любой с ограничениями на оператор сравнения, в Java — реализующий интерфейс Comparable, и так далее.

Магия клея и ножниц

На повестке дня насущные вопросы — как работать с декартовым деревом. Вопрос о том, как же его вообще строить из сырого набора ключей, я немного отложу, а пока что предположим, что какая-то добрая душа начальное дерево нам уже построила, и теперь нам требуется его по необходимости менять.

Вся подноготная работы с декартовым деревом заключается в двух основных операциях: Merge и Split. С помощью них элементарно выражаются все остальные популярные операции, так что начнем с основ.

Операция Merge принимает на вход два декартовых дерева L и R. От нее требуется слить их в одно, тоже корректное, декартово дерево T. Следует заметить, что работать операция Merge может не с любыми парами деревьев, а только с теми, у которых все ключи одного дерева ( L ) не превышают ключей второго ( R ). (Обратите особое внимание на это условие — оно нам еще не раз пригодится в будущем!)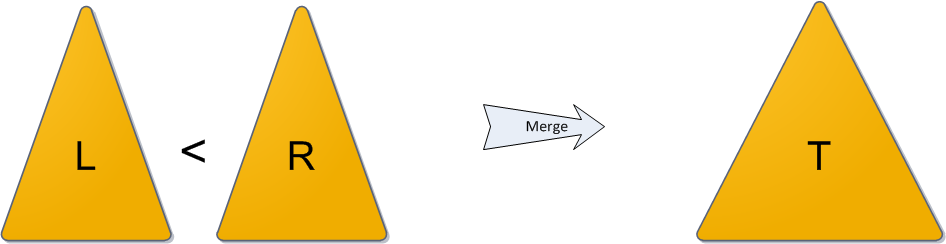


Алгоритм работы Merge очень прост. Какой элемент станет корнем будущего дерева? Очевидно, с наибольшим приоритетом. Кандидатов на максимальный приоритет у нас два — только корни двух исходных деревьев. Сравним их приоритеты; пускай для однозначности приоритет y левого корня больше, а ключ в нем равен x. Новый корень определен, теперь стоит подумать, какие же элементы окажутся в его правом поддереве, а какие — в левом.

Легко понять, что все дерево R окажется в правом поддереве нового корня, ведь ключи-то у него больше x по условию. Точно так же левое поддерево старого корня L.Left имеет все ключи, меньшие x, и должно остаться левым поддеревом, а правое поддерево L.Right… а вот правое должно по тем же соображениям оказаться справа, однако неясно, куда тогда ставить его элементы, а куда элементы дерева R?

Стоп, почему неясно? У нас есть два дерева, ключи в одном меньше ключей в другом, и нам нужно их как-то объединить и полученный результат привесить к новому корню как правое поддерево. Просто рекурсивно вызываем Merge для L.Right и дерева R, и возвращенное ею дерево используем как новое правое поддерево. Результат налицо.

На рисунке синим цветом показано правое поддерево результирующего дерева после операции Merge и связь от нового корня к этому поддереву.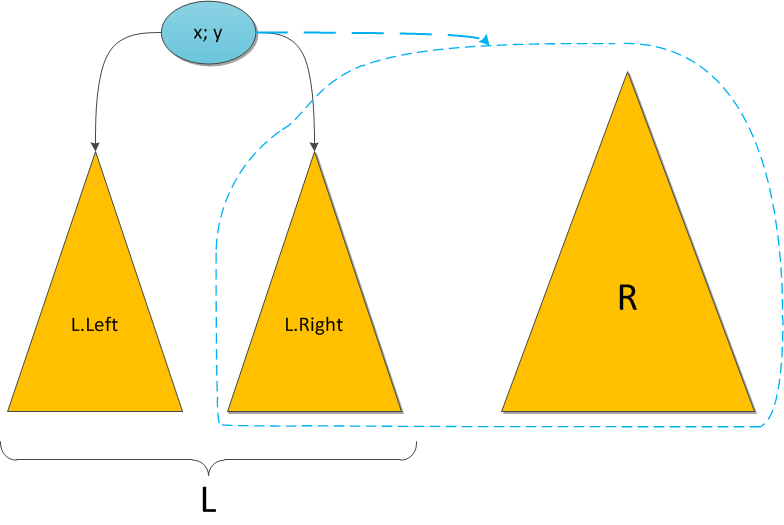

Симметричный случай — когда приоритет в корне дерева R выше — разбирается аналогично. И, конечно, надо не забыть про основу рекурсии, которая в нашем случае наступает, если какое-то из деревьев L и R, или сразу оба, являются пустыми.

Исходный код Merge:

public static Treap Merge(Treap L, Treap R)

{

if (L == null) return R;

if (R == null) return L;
if (L.y > R.y)

{

var newR = Merge(L.Right, R);

return new Treap(L.x, L.y, L.Left, newR);

}

else

{

var newL = Merge(L, R.Left);

return new Treap(R.x, R.y, newL, R.Right);

}

}

Теперь об операции Split. На вход ей поступает корректное декартово дерево T и некий ключ x₀. Задача операции — разделить дерево на два так, чтобы в одном из них ( L ) оказались все элементы исходного дерева с ключами, меньшими x₀, а в другом ( R ) — с большими. Никаких особых ограничений на дерево не накладывается.
Двоичная куча представляет собой полное бинарное дерево, для которого выполняется основное свойство кучи: приоритет каждой вершины больше приоритетов её потомков. В простейшем случае приоритет каждой вершины можно считать равным её значению. В таком случае структура называется max-heap, поскольку корень поддерева является максимумом из значений элементов поддерева. В этой статье для простоты используется именно такое представление. Напомню также, что дерево называется полным бинарным, если у каждой вершины есть не более двух потомков, а заполнение уровней вершин идет сверху вниз 

Двоичную кучу удобно хранить в виде одномерного массива, причем левый потомок вершины с индексом i имеет индекс 2*i+1, а правый 2*i+2. Корень дерева – элемент с индексом 0. Высота двоичной кучи равна высоте дерева, то есть log₂ N, где N – количество элементов массива.
Новый элемент добавляется на последнее место в массиве, то есть позицию с индексом heapSize:

Иначе говоря, новый элемент «всплывает», «проталкивается» вверх, пока не займет свое место. Сложность алгоритма не превышает высоты двоичной кучи (так как количество «подъемов» не больше высоты дерева), то есть равна O(log₂ N).

Наиболее очевидный способ построить кучу из неупорядоченного массива – это по очереди добавить все его элементы. Временная оценка такого алгоритма O(N log₂ N). Однако можно построить кучу еще быстрее — за О(N). Сначала следует построить дерево из всех элементов массива, не заботясь о соблюдении основного свойства кучи, а потом вызвать метод heapify для всех вершин

Таким образом, двоичная куча имеет структуру дерева логарифмической высоты (относительно количества вершин), позволяет за логарифмическое же время добавлять элементы и извлекать элемент с максимальным приоритетом за константное время. В то же время двоичная куча проста в реализации и не требует дополнительной памяти.
Очередь с приоритетом (англ. priority queue) — абстрактный тип данных в программировании, поддерживающий две обязательные операции — добавить элемент и извлечь максимум^[1] (минимум). Предполагается, что для каждого элемента можно вычислить его приоритет — действительное число или в общем случае элемент линейно упорядоченного множества

Основные методы, реализуемые очередью с приоритетом, следующие^[2][3][1]:

• 
  insert(ключ, значение) — добавляет пару (ключ, значение) в хранилище;
  
• 
  extract_minimum() — возвращает пару (ключ, значение) с минимальным значением ключа, удаляя её из хранилища.
  

При этом меньшее значение ключа соответствует более высокому приоритету.

В некоторых случаях более естественен рост ключа вместе с приоритетом. Тогда второй метод можно назвать extract_maximum()^[1].

Есть ряд реализаций, в которых обе основные операции выполняются в худшем случае за время, ограниченное {\displaystyle O(\log n)}

В качестве примера очереди с приоритетом можно рассмотреть список задач работника. Когда он заканчивает одну задачу, он переходит к очередной — самой приоритетной (ключ будет величиной, обратной приоритету) — то есть выполняет операцию извлечения максимума. Начальник добавляет задачи в список, указывая их приоритет, то есть выполняет операцию добавления элемента.


Судоку, кроссворд, 6 ферзей.

Итак, жадный алгоритм (greedy algorithm) — это алгоритм, который на каждом шагу делает локально наилучший выбор в надежде, что итоговое решение будет оптимальным.
К примеру, алгоритм Дейкстры нахождения кратчайшего пути в графе вполне себе жадный, потому что мы на каждом шагу ищем вершину с наименьшим весом, в которой мы еще не бывали, после чего обновляем значения других вершин. При этом можно доказать, что кратчайшие пути, найденные в вершинах, являются оптимальными.

К слову, алгоритм Флойда, который тоже ищет кратчайшие пути в графе (правда, между всеми вершинами), не является примером жадного алгоритма. Флойд демонстрирует другой метод — метод динамического программирования.

Сам по себе жадный алгоритм реализуется примерно вот так:

 //отсортируем по весу
 //вначале ответом будет пустое множество
for   to 
   if   then //если подходит
        //то включаем в множество
о кодировании Хаффмана.

Метод основывается на создании бинарных деревьев. В нем узел может быть либо конечным, либо внутренним. Изначально все узлы считаются листьями (конечными), которые представляют сам символ и его вес (то есть частоту появления). Внутренние узлы содержат вес символа и ссылаются на два узла-наследника. По общему соглашению, бит «0» представляет следование по левой ветви, а «1» — по правой. В полном дереве N листьев и N-1 внутренних узлов. Рекомендуется, чтобы при построении дерева Хаффмана отбрасывались неиспользуемые символы для получения кодов оптимальной длины.

Мы будем использовать очередь с приоритетами для построения дерева Хаффмана, где узлу с наименьшей частотой будет присвоен высший приоритет. Ниже описаны шаги построения:

1. 
   Создайте узел-лист для каждого символа и добавьте их в очередь с приоритетами.
   
2. 
   Пока в очереди больше одного листа делаем следующее:
   
   
   • 
     Удалите два узла с наивысшим приоритетом (с самой низкой частотой) из очереди;
     
   • 
     Создайте новый внутренний узел, где эти два узла будут наследниками, а частота появления будет равна сумме частот этих двух узлов.
     
   • 
     Добавьте новый узел в очередь приоритетов.
     
3. 
   Единственный оставшийся узел будет корневым, на этом построение дерева закончится.
   

Поразрядная сортировка Вычислительная сложность O(N).

Быстрая сортировка

разбился на 2 части: левая часть содержит элементы, которые меньше этого элемента, а правая часть содержит элементы, которые больше или равны этого элемента. Такой разделяющий элемент называется пивотом.

Пивот в нашем случае выбирается случайным образом. Такой алгоритм называется рандомизированным. На самом деле пивот можно выбирать самым разным образом: либо брать случайный элемент, либо брать первый / последний элемент учаcтка, либо выбирать его каким-то «умным» образом.

Временная сложность алгоритма выражается через нее же по формуле: T(n) = n + T(a * n) + T((1 — a) * n). Таким образом, когда мы вызываем сортировку массива из n элементов, тратится порядка n операций на выполнение partition'а и на выполнения себя же 2 раза с параметрами a * n и (1 — a) * n, потому что пивот разделил элемент на доли.

В лучшем случае a = 1 / 2, то есть пивот каждый раз делит участок на две равные части. В таком случае: T(n) = n + 2 * T(n / 2) = n + 2 * (n / 2 + 2 * T(n / 4)) = n + n + 4 * T(n / 4) = n + n + 4 * (n / 4 + 2 * T(n / 8)) = n + n + n + 8 * T(n / 8) =…. Итого будет log(n) слагаемых, потому как слагаемые появляются до тех пор, пока аргумент не уменьшится до 1. В результате T(n) = O(n * log(n)).

В худшем случае a = 1 / n, то есть пивот отсекает ровно один элемент. В первой части массива находится 1 элемент, а во второй n — 1. То есть: T(n) =n + T(1) + T(n — 1) = n + O(1) + T(n — 1) = n + O(1) + (n — 1 + O(1) + T(n — 2)) = O(n^2). Квадрат возникает из-за того, что он фигурирует в формуле суммы арифметической прогрессии, которая появляется в процессе расписывания формулы.

В среднем в идеале надо считать математическое ожидание различных вариантов. Можно показать, что если пивот делит массив в отношении 1:9, то итоговая асимптотика будет все равно O(n * log(n)).

Сортировка слиянием

Сортировки слиянием работают по такому принципу:

1. 
   Ищутся (как вариант — формируются) упорядоченные подмассивы.
   
2. 
   Упорядоченные подмассивы соединяются в общий упорядоченный подмассив.
   

Сам по себе какой-нибудь упорядоченный подмассив внутри массива не имеет особой ценности. Но если в массиве мы найдём два упорядоченных подмассива, то это совершенно другое дело. Дело в том, что очень быстро и с минимальными затратами можно произвести над ними слияние — сформировать из пары упорядоченных подмассивов общий упорядоченный подмассив.



Мы можем получить T (n) = 2 ^ kT (n / 2 ^ k) + kn. Когда T (n / 2 ^ k) = T (1), то есть n / 2 ^ k = 1, мы получаем k = log2n. Подставляем значение k в приведенную выше формулу и получаем T (n) = Cn + nlog2n. Если для представления мы используем большую нотацию O, T (n) равно O (nlogn). Таким образом, временная сложность сортировки слиянием составляет O (nlogn).

Пирамидальная сортировка (или сортировка кучей, HeapSort) — это метод сортировки сравнением, основанный на такой структуре данных как двоичная куча. Она похожа на сортировку выбором, где мы сначала ищем максимальный элемент и помещаем его в конец. Далее мы повторяем ту же операцию для оставшихся элементов.

1. 
   Постройте max-heap из входных данных.
   
2. 
   На данном этапе самый большой элемент хранится в корне кучи. Замените его на последний элемент кучи, а затем уменьшите ее размер на 1. Наконец, преобразуйте полученное дерево в max-heap с новым корнем.
   
3. 
   Повторяйте вышеуказанные шаги, пока размер кучи больше 1.
   

Временная сложность: Временная сложность heapify — O(Logn). Временная сложность createAndBuildHeap() равна O(n), а общее время работы пирамидальной сортировки — O(nLogn)
Алгоритм Кнута-Морриса-Пратта используется для поиска подстроки (образца) в строке. Кажется, что может быть проще: двигаемся по строке и сравниваем последовательно символы с образцом. Не совпало, перемещаем начало сравнения на один шаг и снова сравниваем. И так до тех пор, пока не найдем образец или не достигнем конца строки.

Идея КМП-поиска – при каждом несовпадении двух символов текста и образа образ сдвигается на все пройденное расстояние, так как меньшие сдвиги не могут привести к полному совпадению.

Особенности КМП-поиска:
1. требуется порядка (N+M) сравнений символов для получения результата;
2. схема КМП-поиска дает подлинный выигрыш только тогда, когда неудаче предшествовало некоторое число совпадений. Лишь в этом случае образ сдвигается более чем на единицу. К несчастью совпадения встречаются значительно реже чем несовпадения. Поэтому выигрыш от КМП-поиска в большинстве случаев текстов весьма незначителен.

Алгоритм Рабина — Карпа — это алгоритм поиска строки, который ищет шаблон, то есть подстроку, в тексте, используя хеширование.

алгоритм Рабина — Карпа пытается ускорить проверку эквивалентности образца с подстроками в тексте, используя хеш-функцию. Хеш-функция — это функция, преобразующая каждую строку в числовое значение, называемое хеш-значением (хеш); например, мы можем иметь хеш от строки «hello» равным 5. Алгоритм использует тот факт, что если две строки одинаковы, то и их хеш-значения также одинаковы. Таким образом, всё что нам нужно, это посчитать хеш-значение искомой подстроки и затем найти подстроку с таким же хеш-значением.

Однако существуют две проблемы, связанные с этим. Первая состоит в том, что, так как существует очень много различных строк, между двумя различными строками может произойти коллизия — совпадение их хешей. В таких случаях необходимо посимвольно проверять совпадение самих подстрок, что занимает достаточно много времени, если данные подстроки имеют большую длину (эту проверку делать не нужно, если ваше приложение допускает ложные срабатывания). При использовании достаточно хороших хеш-функций (смотрите далее) коллизии случаются крайне редко, и в результате среднее время поиска оказывается невелико.

Алгоритм Рабина-Карпа имеет сложность O (nm), где n, конечно, является длиной текста, а m — длиной шаблона


n

T
, суммарное время работы алгоритма будет равно O(m+n{\displaystyle \displaystyle \Theta (m+n)}, где {\displaystyle n}  — длина текста {\displaystyle \displaystyle T} .

Понятие хеш-таблицы

Хеш-таблица — это контейнер, который используют, если хотят быстро выполнять операции вставки/удаления/нахождения. В языке C++ хеш-таблицы скрываются под флагом unoredered_set и unordered_map. В Python вы можете использовать стандартную коллекцию set — это тоже хеш-таблица.
Реализация у нее, возможно, и не очевидная, но довольно простая, а главное — как же круто использовать хеш-таблицы, а для этого лучше научиться, как они устроены.


Для начала объяснение в нескольких словах. Мы определяем функцию хеширования, которая по каждому входящему элементу будет определять натуральное число. А уже дальше по этому натуральному числу мы будем класть элемент в (допустим) массив. Тогда имея такую функцию мы можем за O(1) обработать элемент.


Теперь стало понятно, почему же это именно хеш-таблица.

Проблема коллизии

Естественно, возникает вопрос, почему невозможно такое, что мы попадем дважды в одну ячейку массива, ведь представить функцию, которая ставит в сравнение каждому элементу совершенно различные натуральные числа просто невозможно. Именно так возникает проблема коллизии, или проблемы, когда хеш-функция выдает одинаковое натуральное число для разных элементов.


Существует несколько решений данной проблемы: метод цепочек и метод двойного хеширования. В данной статье я постараюсь рассказать о втором методе, как о более красивом и, возможно, более сложном.

Решения проблемы коллизии методом двойного хеширования

Мы будем (как несложно догадаться из названия) использовать две хеш-функции, возвращающие взаимопростые натуральные числа.


Одна хеш-функция (при входе g) будет возвращать натуральное число s, которое будет для нас начальным. То есть первое, что мы сделаем, попробуем поставить элемент g на позицию s в нашем массиве. Но что, если это место уже занято? Именно здесь нам пригодится вторая хеш-функция, которая будет возвращать t — шаг, с которым мы будем в дальнейшем искать место, куда бы поставить элемент g.


Мы будем рассматривать сначала элемент s, потом s + t, затем s + 2*t и т.д. Естественно, чтобы не выйти за границы массива, мы обязаны смотреть на номер элемента по модулю (остатку от деления на размер массива).


Наконец мы объяснили все самые важные моменты, можно перейти к непосредственному написанию кода, где уже можно будет рассмотреть все оставшиеся нюансы. Ну а строгое математическое доказательство корректности использования двойного хеширования можно найти тут.