ответы сессия довгалюк 2 семестр. Определение Правосторонний бинарный поиск

Название	Определение Правосторонний бинарный поиск
Анкор	ответы сессия довгалюк 2 семестр
Дата	10.02.2022
Размер	3.01 Mb.
Формат файла
Имя файла	Algoritmy.docx
Тип	Документы #357616
страница	6 из 11

1 2 3 4 5 6 7 8 9 10 11

Реализация

Реализовать представленный алгоритм проще всего с помощью СНМ(система непересекающихся отрезков).

Вначале, как мы уже раннее говорили, необходимо отсортировать ребра по неубыванию по их весам. Далее с помощью вызовов функции make_set()мы каждую вершину можем поместить в свое собственное дерево, то есть, создаем некоторое множество подграфов. Дальше итерируемся по всем ребрам в отсортированном порядке и смотрим, принадлежат ли инцидентные вершины текущего ребра разным подграфам с помощью функции find_set() или нет, если оба конца лежат в разных компонентах, то объединяем два разных подграфа в один с помощью функции union_sets().

В итоге асимптотическая сложность данного алгоритма сводится к:

O(E log V)

sort() -

O(E log V)
make_set()-

O(V)
find_set -

O(1)
union_sets -

O(1)

Система непересекающихся множеств и её применения

Алгоритмы *

система непересекающихся множеств. Она же известна под названиями disjoint set union (DSU) или Union-Find.

Условие

Поставим перед собой следующую задачу. Пускай мы оперируем элементами N видов (для простоты, здесь и далее — числами от 0 до N-1). Некоторые группы чисел объединены в множества. Также мы можем добавить в структуру новый элемент, он тем самым образует множество размера 1 из самого себя. И наконец, периодически некоторые два множества нам потребуется сливать в одно.

Формализируем задачу: создать быструю структуру, которая поддерживает следующие операции:

MakeSet(X) — внести в структуру новый элемент X, создать для него множество размера 1 из самого себя.
Find(X) — возвратить идентификатор множества, которому принадлежит элемент X. В качестве идентификатора мы будем выбирать один элемент из этого множества — представителя множества. Гарантируется, что для одного и того же множества представитель будет возвращаться один и тот же, иначе невозможно будет работать со структурой: не будет корректной даже проверка принадлежности двух элементов одному множеству if (Find(X) == Find(Y)).
Unite(X, Y) — объединить два множества, в которых лежат элементы X и Y, в одно новое.

На рисунке я продемонстрирую работу такой гипотетической структуры.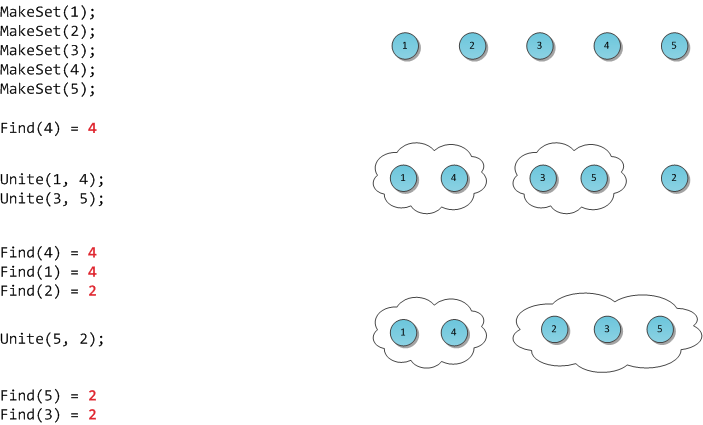

Реализация

Классическая реализация DSU была предложена Bernard Galler и Michael Fischer в 1964 году, однако исследована (включая временную оценку сложности) Робертом Тарьяном уже в 1975. Тарьяну же принадлежат некоторые результаты, улучшения и применения, о которых мы сегодня ещё поговорим.

Хранить структуру данных будем в виде леса, то есть превратим DSU в систему непересекающихся деревьев. Все элементы одного множества лежат в одном соответствующем дереве, представитель дерева — его корень, слияние множеств суть просто объединение двух деревьев в одно. Как мы увидим, такая идея вкупе с двумя небольшими эвристиками ведет к поразительно высокому быстродействию получившейся структуры.

Для начала нам потребуется массив p, хранящий для каждой вершины дерева её непосредственного предка (а для корня дерева X — его самого). С помощью одного только этого массива можно эффективно реализовать две первые операции DSU:

MakeSet(X)

Чтобы создать новое дерево из элемента X, достаточно указать, что он является корнем собственного дерева, и предка не имеет.
public void MakeSet(int x)

{

p[x] = x;

}

Find(X)

Представителем дерева будем считать его корень. Тогда для нахождения этого представителя достаточно подняться вверх по родительским ссылкам до тех пор, пока не наткнемся на корень.

Но это еще не все: такая наивная реализация в случае вырожденного (вытянутого в линию) дерева может работать за O(N), что недопустимо. Можно было бы попытаться ускорить поиск. Например, хранить не только непосредственного предка, а большие таблицы логарифмического подъема вверх, но это требует много памяти. Или хранить вместо ссылки на предка ссылку на собственно корень — однако тогда при слиянии деревьев (Unite) придется менять эти ссылки всем элементам одного из деревьев, а это опять-таки временные затраты порядка O(N).

Мы пойдем другим путём: вместо ускорения реализации будем просто пытаться не допускать чрезмерно длинных веток в дереве. Это первая эвристика DSU, она называется сжатие путей (path compression). Суть эвристики: после того, как представитель таки будет найден, мы для каждой вершины по пути от X к корню изменим предка на этого самого представителя. То есть фактически переподвесим все эти вершины вместо длинной ветви непосредственно к корню. Таким образом, реализация операции Find становится двухпроходной.

На рисунке показано дерево до и после выполнения операции Find(3). Красные ребра — те, по которым мы прошлись по пути к корню. Теперь они перенаправлены. Заметьте, как после этого кардинально уменьшилась высота дерева.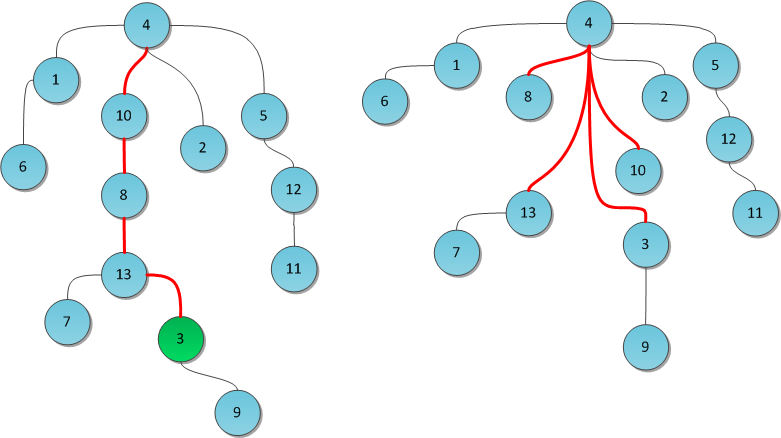

Исходный код в рекурсивной форме написать достаточно просто:
public int Find(int x)

{

if (p[x] == x) return x;

return p[x] = Find(p[x]);

}

Unite(X, Y)

Со слиянием двух деревьев придется чуть повозиться. Найдем для начала корни обоих сливаемых деревьев с помощью уже написанной функции Find. Теперь, помня, что наша реализация хранит только ссылки на непосредственных родителей, для слияния деревьев достаточно было бы просто подвесить один из корней (а с ним и все дерево) сыном к другому. Таким образом все элементы этого дерева автоматически станут принадлежать другому — и процедура поиска представителя будет возвращать корень нового дерева.

Встает вопрос: какое дерево к какому подвешивать? Всегда выбирать какое-то одно, скажем, дерево X, не годится: легко подобрать пример, на котором после N объединений мы получим вырожденное дерево — одну ветку из N элементов. И тут в ход вступает вторая эвристика DSU, направленная на уменьшение высоты деревьев.

Будем хранить помимо предков еще один массив Rank. В нем для каждого дерева будет храниться верхняя граница его высоты — то есть длиннейшей ветви в нем. Заметьте, не сама высота — в процессе выполнения Find длиннейшая ветвь может самоуничтожиться, а тратить еще итерации на нахождение новой длиннейшей ветви слишком дорого. Поэтому для каждого корня в массиве Rank будет записано число, гарантированно больше или равное высоте его дерева.

Теперь легко принять решении о слиянии: чтобы не допустить слишком длинных ветвей в DSU, будем подвешивать более низкое дерево к более высокому. Если их высоты равны — не играет роли, кого подвешивать к кому. Но в последнем случае новоиспеченному корню надо не забыть увеличить Rank.

Вот так производится типичный Unite (например, с параметрами 8 и 19):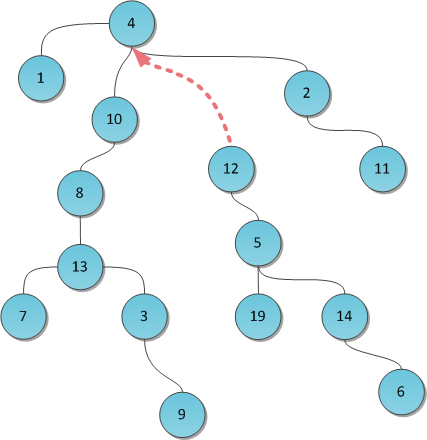

Однако на практике оказывается, что можно и не тратить дополнительные O(N) памяти на махинации с рангами. Достаточно выбирать корень для переподвешивания случайным образом — как ни удивительно, но такое решение дает на практике скорость, вполне сравнимую с оригинальной ранговой реализацией. Автор данной статьи всю жизнь пользуется именно рандомизированным DSU, и еще не было случая, когда тот бы подвёл.

Быстродействие

В силу применения двух эвристик скорость работы каждой операции сильно зависит от структуры дерева, а структура дерева — от списка выполненных до того операций. Исключение составляет только MakeSet — её время работы очевидно O(1) :-) Для остальных двух скорость очень неочевидна.

Роберт Тарьян доказал в 1975 г. замечательный факт: время работы как Find, так и Unite на лесе размера N есть O(α(N)).
Под α(N) в математике обозначается обратная функция Аккермана, то есть, функция, обратная для f(N) = A(N, N). Функция Аккермана A(N, M) известна тем, что у нее колоссальная скорость роста. К примеру, A(4, 4) = 2²²⁶⁵⁵³⁶-3, это число поистине огромно. Вообще, для всех мыслимых практических значений N обратная функция Аккермана от него не превысит 5. Поэтому её можно принять за константу и считать O(α(N)) ≅ O(1).

Итак, имеем:
MakeSet(X) — O(1).
Find(X) — O(1) амортизированно.
Unite(X, Y) — O(1) амортизированно.
Расход памяти — O(N).

Совсем неплохо :-)

Практические применения

Для DSU известно большое число различных использований. Большинство связано с решением некоторой задачи в режиме оффлайн — то есть когда список запросов касательно структуры, которые поступают программе, известен заранее. Я приведу здесь несколько таких задач вместе с краткими идеями решений.

Рандомизированное двоичное дерево поиска

Основное свойство дерева поиска — любой ключ в левом поддереве меньше корневого ключа, а в правом поддереве — больше корневого ключа (для ясности изложения будем считать, что все ключи различны).

Пусть TT — бинарное дерево поиска. Тогда

Если TT пусто, то оно является рандомизированным бинарным деревом поиска.
Если TT непусто (содержит nn вершин, n>0n>0), то TT — рандомизированное бинарное дерево поиска тогда и только тогда, когда его левое и правое поддеревья (LL и RR) оба являются RBST, а также выполняется соотношение P[size(L)=i]=1n,i=1..nP[size(L)=i]=1n,i=1..n.
Похожие идеи используются в декартовом дереве, поэтому во многих русскоязычных ресурсах термин рандомизированное бинарное дерево поиска используется как синонимическое название декартового дерева и декартового дерева по неявному ключу.
Операции обхода дерева, поиска ключа, поиска максимума/минимума, поиск следующего/предыдущего элемента выполняются как в обычном дереве поиска, т.к. не меняют структуру дерева.

1 2 3 4 5 6 7 8 9 10 11