Под управлением будем понимать совокупность мероприятий по организации процесса для достижения поставленной цели.
Под объектом управления будем понимать часть окружающей среды выделенную таким образом, что выполняются два условия:
- на объект можно воздействовать, это воздействие в дальнейшем будем называть управляющим,
- управляющее воздействие меняет состояние объекта в необходимом для достижения поставленной цели направлении.

Необходимые составляющие процесса управления рассмотрим на примере движения судна см.рис.1.1 [6], [7].
Рис.1.1
Целью процесса управления в данном случае является поддержание объектом управления (ОУ) заданного курса з. При движении ОУ (судно) подвергается возмущающему воздействию fв (волны, порывы ветра), в результате чего текущий курс в некоторый момент времени будет отличаться от заданного з. Информация о цели и о текущем состоянии процесса управления поступает на управляющее устройство (УУ). В УУ сравниваются цель и текущее состояние, оценивается их рассогласование и вырабатывается управляющее воздействие на регулирующий орган ОУ. В данном случае регулирующий орган ОУ – руль; управляющее воздействие – угол поворота руля.
УУ “принимает решение”, т.е. вырабатывает управляющее воздействие на основе величины рассогласования и в соответствии с определенным алгоритмом – законом управления. Управляющее воздействие должно минимизировать рассогласование между целью и состоянием процесса управления с заданной точностью и за требуемое время.
Рассмотренный пример содержит все необходимые аспекты, то есть все перечисленные ниже составляющие процесса управления любым объектом.
1. Наличие четко формализованной цели управления. В данном случае это требуемый курс судна з.
2. Контроль за текущим состоянием процесса управления. В данном случае это истинный курс судна .
3. Сопоставление цели и состояния процесса, оценка рассогласования и принятие решения, то есть выработка управляющего воздействия.
4. Исполнение решения – непосредственное действие на регулирующий орган ОУ.
Отсутствие хотя бы одной из перечисленных составляющих или их неправильная организация делают невозможным осуществление процесса управления либо вообще, либо с недостаточно высоким качеством.
Для организации процесса управления конкретным объектом помимо УУ необходимы измерительные устройства для получения информации о текущем состоянии, а также усилительно-преобразовательные устройства и исполнительные механизмы, назначением которых является согласование сигналов по физической природе, по мощности и динамическому диапазону.
Для графического представления структуры систем управления используются два типа схем: функциональные и структурные. В функциональных схемах каждому элементу соответствуют различные технические устройства упомянутые выше. Пример функциональной схемы приведен на рисунке:
fв
               
Ум
СУ
y
fy
ОУ
Р
У
с
СУ1
контур МОС
ку
Контур главной обратной связи ( ГОС)
где приняты обозначения: ОУ- объект управления, СУ – сравнивающие устройства, У- усилитель, Р – регулятор, Ум – усилитель мощности, Ку – корректирующее устройство, МОС – местная обратная связь, ГОС – главная обратная связь.
На структурной схеме все элементы описываются некоторыми математическими операторами.
Все эти взаимосвязанные и взаимодействующие функциональные устройства в совокупности с ОУ и образуют систему управления (СУ).
В дальнейшем могут рассматриваться объекты управления разнообразной физической природы: электрические, механические, гидравлические и другие. В частности, можно рассмотреть такие объекты как аэродинамические (самолет, ракета), или механические (автомобиль) Анализируя процессы управления в автопилоте воздушного судна или в системе авторулевого автомобиля придем к выводу, что они включают все перечисленные выше аспекты.
Наука занимающаяся разработкой методов эффективного управления объектами различной физической природы называется теорией управления.
1.2. Принципы управления
Несмотря на многообразие ОУ, можно сформулировать лишь несколько основополагающих принципов управления [1], [4], [6], [7]. Реализация того или иного принципа управления определяет вид общей структуры СУ.


Рис.1.2
Независимо от того, как организован процесс управления, в любой СУ должен присутствовать прямой канал передачи управляющего воздействия fу к той выходной координате y, которая должна это управляющее воздействие “воспроизводить” –рис.1.2. Пусть известны математические операторы связывающие все сигналы на схеме Рис.1.2. В простейшем случае допустим, что это постоянные коэффициенты: 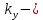 коэффициент передачи УУ. коэффициент передачи УУ. - - 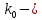 коэффициент передачи объекта управления по управляющему входу, коэффициент передачи объекта управления по управляющему входу, 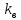 – коэффициент передачи объекта по возмущению. – коэффициент передачи объекта по возмущению.
Здесь изображена укрупненная структура; ОУ может содержать усилительные, преобразовательные и другие функциональные звенья.
Принципы управления разделяются по способу контроля за текущим состоянием процесса управления.
Принцип разомкнутого управления. Структура на рис.1.2 собственно и реализует этот принцип. По существу, здесь не производится учет текущей информации о состоянии процесса управления. В этом случае для выходного сигнала справедливо выражение:
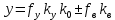
Очевидно, что второе слагаемое есть не что иное,
как величина ошибки обусловленной действием возмущения. Принцип разомкнутого управления может быть использован только в тех случаях, когда сигнальное возмущающее воздействие fв незначительно, вариации параметров (параметрические возмущения) всех функциональных устройств также малы, математическое описание СУ известно и достоверно, а требования к качеству процесса управления не слишком высоки. Таким образом, использование принципа разомкнутого управления ограничено.
Принцип компенсации. При реализации принципа компенсации учет информации о текущем состоянии процесса управления производится путем непосредственного измерения возмущающего воздействия –см.рис.1.3,где ИУ – измерительное устройство.


Рис.1.3
Структурной особенностью СУ, реализующих принцип компенсации, является наличие на структурной схеме модели дополнительного пути прохождения возмущающего воздействия. Обозначим коэффициент передачи ИУ -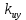 . Тогда выбирая соответствующие знаки суммирования сигналов можно записать: . Тогда выбирая соответствующие знаки суммирования сигналов можно записать:
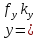 - - 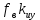 ) )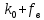 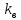 . .
Выберем соответствующее значение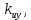 чтобы чтобы 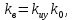 при котором значение возмущения равно нулю, так как второе и третье слагаемые компенсируются.0 при котором значение возмущения равно нулю, так как второе и третье слагаемые компенсируются.0
Принцип компенсации возмущения используется в тех случаях, когда имеется глобальное (по сравнению с другими) и поддающееся измерению сигнальное возмущение.
Очевидно, что влияние параметрических возмущений и неопределенность параметров операторов функциональных звеньев в данном случае не учитываются, не ослабляются и непосредственно ухудшают качество процесса управления.

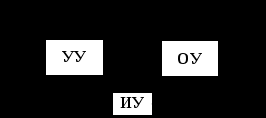
Рис.1.4
Принцип замкнутого управления. При реализации этого принципа учет информации о текущем состоянии процесса управления производится путем непосредственного измерения управляемой координаты –см.рис.1.4.
Структурной особенностью СУ, реализующих принцип замкнутого управления, является наличие на
структурной схеме модели системы замкнутого пути – контура, образуемого при передаче текущей информации от управляемой координаты к УУ. Поэтому такой принцип управления называется также принципом обратной связи, при котором причина (управляющее воздействие) ставится в зависимость от следствия (выходная координата y) которое она вызывает.
Существенной особенностью замкнутого управления является то обстоятельство, что не имеют значения причины, вызвавшие отклонение процесса от цели управления. Ими могут являться множество сигнальных и параметрических возмущений, неточность математического описания функциональных звеньев. В связи с этим рассматриваемый принцип более универсален и получил широкое распространение.
На простейшем примере рассмотрим влияние обратной связи на качество управления. Преобразуем исходную структуру на Рис. 1.4 введя понятие суммирующего устройства (в дальнейшем СУ)
 СУ СУ


fв
С учетом введенных элементов исходная структура на рис.1.4 может быть преобразована к следующему виду:
  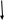  
e
y
µ
fу
ОУ
УУ
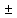

xос
  
ИУ
Приняты следующие обозначения:
- ОУ – объект управления, с выходным сигналом y(t), на объект воздействуют два сигнала –управляющее воздействие µ(t) и сигнал возмущения fв(t). Как и ранее допустим, что коэффициент передачи объекта по управляющему входу равен k0, а по возмущению - kв. Тогда для выходного сигнала y(t) справедливо:
y(t)= µ(t)k0 + fв(t)kв.
Такая запись предполагает, что сигналы на выходе объекта взаимодействуют аддитивно, то есть суммируются;
- УУ – управляющее устройство с коэффициентом передачи kу;
- ИУ – измерительное устройство в цепи обратной связи с коэффициентом передачи kиу. Если kиу=1, то обратная связь называется единичной;
- e(t) сигнал на выходе суммирующего устройства.
Заметим, что в суммирующем устройстве входные сигналы могут как суммироваться (тогда обратная связь называется положительной), так и вычитаться (тогда обратная связь называется отрицательной). В дальнейшем рассматриваются системы только с отрицательной обратной связью.
С учетом введенных обозначений и полагая обратную связь единичной (т.е. kиу=1) можно записать систему уравнений:
e(t) = fу(t) – y(t),
y(t) = µ(t) k0 + fв(t) kв
µ(t) = e(t) kу
Исключая промежуточные переменные e(t) и µ(t) получим:
y(t) = 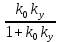 fу(t) + fу(t) +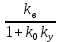 fв(t) fв(t)
Коэффициенты передачи ОУ k0 и kв зависят от физических свойств конкретного объекта и могут считаться конечными и постоянными на интервале управления, а коэффициент УУ kу выбирается на этапе проектирования и может изменяться в широких пределах.
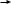 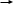 Тогда, если kу ∞, то Тогда, если kу ∞, то 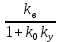 0, а, следовательно, второе слагаемое стремится к нулю, т.е. уменьшается влияние возмущения на выходную координату, 0, а, следовательно, второе слагаемое стремится к нулю, т.е. уменьшается влияние возмущения на выходную координату,
Вывод: отрицательная обратная связь позволяет уменьшить чувствительность системы к возмущающим воздействиям.
Следует отметить, что выработка УУ нового управляющего воздействия для реагирования на изменившееся текущее состояние может произойти только после факта отклонения текущего состояния от цели и появления рассогласования. Поэтому такой принцип управления называется также управлением по отклонению.
Принцип комбинированного управления. Этот принцип является комбинацией (объединением) принципов компенсации и замкнутого управления –см.рис.1.5.

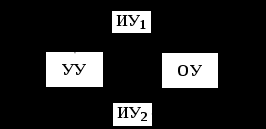
Рис.1.5
Комбинированный принцип целесообразно использовать при высоких требованиях к качеству процесса управления и в том случае, если есть преобладающее и доступное измерению сигнальное возмущение. Это возмущение компенсируется созданием дополнительного пути, а влияние всех остальных неучтенных сигнальных и параметрических возмущений уменьшается контуром отрицательной обратной связи.
1.3. Классификация систем управления
В основе любой классификации лежат признаки, по которым множество объектов подразделяется на подмножества – классы.
Системы управления можно классифицировать по различным признакам. Рассмотрим следующие признаки классификации: информационный, по типу сигналов, алгоритмический, энергетический.
Классификация систем управления по информационному признаку. В этом случае СУ подразделяются по способу получения текущей информации о состоянии процесса управления. Поэтому рассматриваемая классификация подразделяет СУ как раз в соответствии с принципами управления – см.подразд.1.2.
Классификация систем управления по типу сигналов. Используемые в теории управления модели СУ как правило абстрагированы от физической природы сигналов. Сигналы (координаты, переменные) на входах и выходах функциональных звеньев рассматриваются как носители информации, а сами звенья – как преобразователи этих сигналов. Преобразование сигнала некоторым звеном производится в соответствии с приданным (приписанным) этому звену оператором.
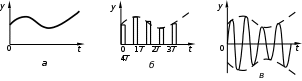
Непрерывные системы. В них информация кодируется уровнем (значением) функции непрерывного времени см.рис.1.6,а.
Рис.1.6
Цифровые системы. В них все переменные или их часть представляют собой дискретные сигналы. Квантование, или дискретизация сигналов может производиться как по уровню, так и по времени. Системы, в которых производится квантование сигнала по времени, а мгновенное значение непрерывного сигнала на выходе какого-либо аналогового звена (звеньев) в моменты квантования кодируется каким-либо параметром импульса (амплитудой, шириной, фазой), называются импульсными системами. На рис.1.6,б приведен пример квантования непрерывного сигнала с одинаковыми периодом следования T и длительностью импульсов, амплитуда которых несет информацию о значениях непрерывного сигнала (так называемая амплитудно-импульсная модуляция).
Системы переменного тока. Информация кодируется амплитудой переменного тока, то есть огибающей несущего сигнала см.рис.1.6,в.

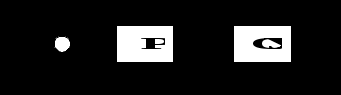
Рис.1.7
Классификация систем управления по алгоритмам управления. На рис.1.7 приведена типовая структура СУ с единичной отрицательной обратной связью. Единичная обратная связь означает, что вся информация о выходной координате передается на элемент сравнения, который образует ошибку рассогласования e(t)=fу(t)y(t). Регулятор P на основе информации об ошибке, т.е. по величине рассогласования цели (задающего воздействия fу(t)) и текущего состояния (управляемой координаты y(t)) вырабатывает управляющее воздействие на ОУ.
Регулятор функционирует в соответствии с заложенным в него алгоритмом, называемым законом управления (законом регулирования).
Рассмотрим наиболее распространенные – типовые законы- управления для непрерывных СУ [4], [6], [7]. Регулятор будем трактовать как преобразователь сигналов в соответствии с некоторым математическим оператором.
Пропорциональный закон (П-закон). Воздействие на объект прямо пропорционально рассогласованию:
(t)=kрe(t). (1.1)
Интегральный закон (И-закон). Уровень воздействия на объект определяется суммарной ошибкой:
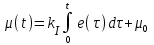 . (1.2) . (1.2)
Если продифференцировать выражение (1.2), то получим соотношение d(t)/dt=kIe(t), которое показывает, что величина ошибки определяет скорость изменения управляющего воздействия. Отличительной особенностью И-закона управления является то обстоятельство, что установившиеся процессы в СУ могут существовать только при e(t)=0.
Пропорционально-интегральный закон (ПИ-закон). Представляет собой комбинацию первых двух:
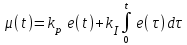 . (1.3) . (1.3)
Пропорционально-интегрально-дифференциальный закон (ПИД-закон). В дополнение к ПИ-закону формирует управляющее воздействие также и с учетом скорости изменения ошибки:
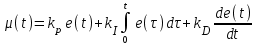 . (1.4) . (1.4)
Рассмотренные типовые законы управления (регулирования) (1.1) – (1.4) часто используются в системах промышленной автоматики.
Классификация систем управления по энергетическому признаку. В зависимости от того, не используется или используется дополнительная (сторонняя) энергия для реализации (исполнения) принятого управляющим устройством решения, СУ подразделяются на системы прямого регулирования и системы непрямого регулирования (управления).
В системах прямого управления отбираемая измерительным устройством энергия достаточна для оказания воздействия на регулирующий орган объекта. При этом часто такие функциональные элементы, как ИУ, УУ (вместе с элементом сравнения) и исполнительный механизм, оказываются конструктивно объединенными. В качестве примера можно указать на две СУ в автомобиле: система стабилизации уровня топлива в поплавковой камере карбюратора, а также система стабилизации температуры охлаждающей жидкости двигателя. Системы прямого регулирования просты и надежны, но применимы с простыми алгоритмами управления и при невысоких требованиях к процессу управления.
В системах непрямого управления функционально разделяются функции измерения (контроля за текущим состоянием процесса), принятия решения управляющим устройством (быть может, по сложному алгоритму) и исполнения решения. Для последней составляющей используются специальные исполнительные устройства и механизмы (сервоприводы), целью которых является преобразование управляющего сигнала по физической природе и усиление по величине и мощности.
По виду используемой энергии различают электрические, механические, гидравлические, электрогидравлические и другие СУ.
1.4. Поведение объектов и систем управления
Теория управления оперирует математическими моделями объектов и СУ, которые описывают поведение систем, то есть их реакцию на управляющие и возмущающие воздействия. Как уже говорилось, функционирующие в этих моделях сигналы (координаты, переменные) в большинстве случаев абстрагированы от их физической природы. Это позволяет описывать и обобщать закономерности поведения в объектах и системах различного функционального назначения.


Рис. 1.8
Поведение объектов управления. Рассмотрим отдельно поведение судна как объекта управления без системы управления, представленной в подразд.1.1, рис.1.1 [6], [7]. Будем считать, что управляющее воздействие на объект не меняется (руль судна закреплен). До момента времени t0 судно двигалось курсом , совпадающим с заданным з – см.рис.1.8. Пусть на этот объект с момента времени t0 и до t1 подействовало постоянное возмущение fв1 (боковой ветер), отклоняющее его с заданного курса з. Отклонение текущего курса от заданного будет возрастать – накапливаться, т.е. интегрироваться. При прекращении действия возмущения (момент времени t1) новый установившийся курс уст не изменится; объект сам по себе не придет в исходное состояние, то есть не вернется к заданному курсу. Такие объекты называются нейтральными, или без самовыравнивания.

 Рис. 1.9 Рис. 1.9
Рассмотрим другой объект – электродвигатель. Будем считать, что на холостом ходу (без нагрузки на валу) на двигатель подано управление, обеспечивающее ему скорость вращения холостого хода nхх – см.рис.1.9. Будем также считать, что управляющее воздействие меняться не будет. В момент времени t0 на валу двигателя произошло изменение нагрузки – момент сопротивления (нагрузки) возрос от Mхх до некоторой величины Mн1. Это вызовет уменьшение скорости вращения, величина которой после окончания переходного процесса примет некоторое значение n1. После сброса нагрузки, то есть после прекращения действия возмущения (момент времени t1) скорость вращения двигателя вернется к значению, существовавшему до приложения возмущения. Считается, что объекты такого типа обладают самовыравниванием и называются устойчивыми.
Приведем пример поведения другого объекта – баллистической ракеты на вертикальном участке активной траектории полета. В плане рассматриваемого процесса аналогами ракеты, “стоящей” на струе газа, являются механический маятник в верхнем положении равновесия, а также длинный шест, поставленный на горизонтальную плоскость. Очевидно, что при любом, даже малом возмущении начнется отклонение объекта от вертикали; это отклонение будет увеличиваться и после прекращения действия возмущения. Такие объекты называются неустойчивыми.
Рассмотрим также поведение маятника, находящегося в нижнем положении равновесия. Возмущающее воздействие отклонит маятник от этого положения на некоторый угол, и после прекращения действия возмущения маятник станет совершать колебательные движения. Про подобные объекты говорят, что они нейтральны, но находятся на колебательной границе устойчивости.
Поведение систем управления. Каждый объект при функционировании должен иметь требуемое поведение. Для нейтрального и, тем более, неустойчивого объекта следует добиться устойчивого поведения. Кроме этого, необходимо обеспечить инвариантность (независимость) или малую чувствительность управляемых координат к сигнальным и параметрическим возмущениям. Например, для рассмотренного примера электродвигателя может быть сформулировано требование в установившемся режиме уменьшить до малой величины (быть может, до нуля) отклонение между nхх и n1 – см.рис.1.9. Переходный процесс как реакция на изменение входных воздействий также должен заканчиваться за требуемое время и быть достаточно плавным.
Для обеспечения требуемого поведения объекта его объединяют с рядом других функциональных звеньев в систему в соответствии с выбранным принципом управления. Такое множество взаимосвязанных звеньев и объекта проявляется при их взаимодействии новым качеством, не присущим отдельно взятому объекту управления – см.подразд.1.1,1.2.
Реакция любой СУ на входное воздействие определяется двумя составляющими: характеристиками входного воздействия и свойствами собственно самой СУ.
На рис.1.10 представлена реакция некоторой устойчивой СУ на входное управляющее воздействие, которое в момент времени t=0 изменяется скачком от нуля до величины fу =Const.
Можно выделить две составляющие реакции СУ на входной сигнал: переходный режим (переходный процесс) и установившийся режим. Время окончания переходного процесса – время регулирования tр – определяют как момент последнего вхождения в некоторую зону, которая обычно составляет 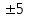 % от установившегося значения yуст (штриховые линии на рис.1.10). % от установившегося значения yуст (штриховые линии на рис.1.10).
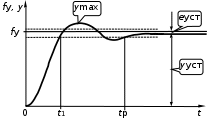
Рис. 1.10
Установившаяся ошибка eуст = fy yуст характеризует точность СУ в установившемся режиме.
Динамика СУ (переходный режим) характеризуется быстродействием системы и склонностью процесса к колебательности.
Склонность к колебательности оценивается перерегулированием
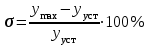 . .

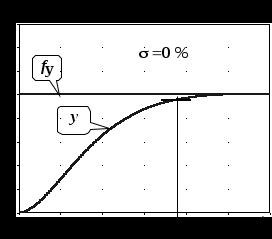
Рис.1.11
Если под быстродействием понимать скорость изменения выходной координаты при реакции на входное воздействие, то может быть также использован показатель качества время первого согласования t1, т.е. время первого вхождения в зону 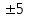 % от установившегося значения yуст. Очевидно, что для процессов с перерегулированием 5%, выполняется tр=t1 см.рис.1.11. Если процесс не имеет перерегулирования, т.е. 0, то процесс называется апериодическим; такой процесс и представлен нарис.1.11. % от установившегося значения yуст. Очевидно, что для процессов с перерегулированием 5%, выполняется tр=t1 см.рис.1.11. Если процесс не имеет перерегулирования, т.е. 0, то процесс называется апериодическим; такой процесс и представлен нарис.1.11.
Для 5% имеем tрt1. При значительной колебательности процесса показатели динамики t1 и tр находятся в противоречии, то есть для достаточно быстродействующей системы время окончания процесса может значительно превосходить время первого согласования – см.рис.1.12.

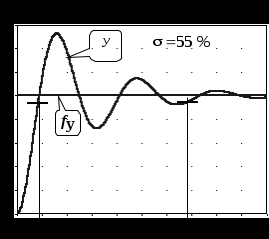
Рис.1.12
Для процессов в СУ, находящихся на границе устойчивости, время регулирования (то есть время окончания процесса) tр =.
Для процессов в неустойчивых СУ рассмотренные показатели качества динамики смысла вообще не имеют.
Типовое поведение систем управления. Несмотря на многообразие объектов различного функционального назначения и систем управления этими объектами, можно описать типовое поведение некоторой “хорошей” СУ. Переходный процесс в такой системе должен быть плавным и либо апериодическим, либо – слабо колебательным – см.рис.1.13. Ограничение на допустимое перерегулирование зависит от требований к конкретной СУ; обычно 1015%. Для некоторых СУ перерегулирование вообще недопустимо и процесс должен быть апериодическим.

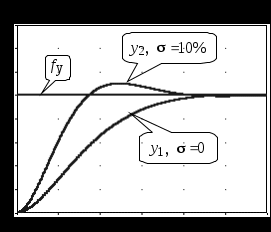 Рис. 1.13 Рис. 1.13
Показанные на рис.1.13 кривые могут быть решением линейного дифференциального уравнения второго порядка, характеристический полином которого имеет пару либо действительных корней (апериодический процесс), либо – пару слабо колебательных комплексно-сопряженных корней (процесс с не значительным перерегулированием). Отсюда следует, что при проектировании даже сложной СУ, содержащей различные динамические звенья и описываемой дифференциальным уравнением достаточно высокого порядка, следует обеспечивать типовое, “простое” поведение, соответствующее поведению системы низкого порядка.
Показатели качества систем управления. Происходящие в динамических системах процессы оцениваются различными показателями качества (критериями), которые характеризуют свойства систем с разных сторон. В этом разделе выше рассмотрены следующие показатели качества: время первого согласования t1, время регулирования tр, перерегулирование, установившаяся ошибка eуст. Все эти критерии оценивают временные процессы, т.е. реакции на входные воздействия и, таким образом, непосредственно характеризуют поведение СУ.
Как будет видно из последующего материала, для расчетов, анализа свойств и обеспечения требуемых характеристик СУ используются модели, представленные не только во временной области, но и в области комплексной переменной “s” преобразования Лапласа, а также модели, отображающие частотные свойства. При использовании всех этих форм представления моделей также вводятся различные оценки и показатели качества.
При проектировании СУ установление взаимосвязи и соответствия различных показателей качества повышает достоверность расчетов и способствует установлению зависимости свойств и характеристик СУ от особенностей внутренней организации и значений параметров отдельных звеньев.
1.5. Задачи теории управления
Основные задачи теории управления – анализ и синтез.
Анализ направлен на выявление свойств поведения СУ и оценку этих свойств с использованием различных критериев – показателей качества. Кроме констатации свойств СУ анализ должен также объяснять зависимость свойств и характеристик от организации системы (ее внутренней структуры), от вида операторов и значений параметров отдельных звеньев.
Синтез направлен на формирование структуры системы для реализации выбранного принципа управления, формирование алгоритма управляющего устройства, а также включает в себя определение и расчет операторов регуляторов и корректирующих звеньев для обеспечения требуемого поведения СУ.
2. ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ МОДЕЛИ И ХАРАКТЕРИСТИКИ
|
 Скачать 1.06 Mb.
Скачать 1.06 Mb.

































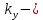 коэффициент передачи УУ.
коэффициент передачи УУ. -
- 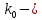 коэффициент передачи объекта управления по управляющему входу,
коэффициент передачи объекта управления по управляющему входу, 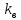 – коэффициент передачи объекта по возмущению.
– коэффициент передачи объекта по возмущению.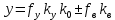


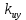 . Тогда выбирая соответствующие знаки суммирования сигналов можно записать:
. Тогда выбирая соответствующие знаки суммирования сигналов можно записать: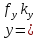 -
- 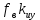 )
)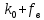
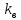 .
.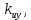 чтобы
чтобы 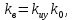 при котором значение возмущения равно нулю, так как второе и третье слагаемые компенсируются.0
при котором значение возмущения равно нулю, так как второе и третье слагаемые компенсируются.0


 СУ
СУ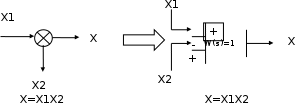




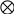







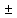


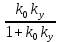 fу(t) +
fу(t) +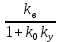 fв(t)
fв(t)
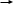 Тогда, если kу ∞, то
Тогда, если kу ∞, то 


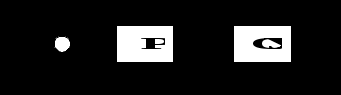
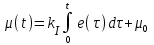 . (1.2)
. (1.2)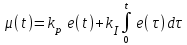 . (1.3)
. (1.3)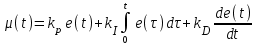 . (1.4)
. (1.4)


 Рис. 1.9
Рис. 1.9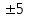 % от установившегося значения yуст (штриховые линии на рис.1.10).
% от установившегося значения yуст (штриховые линии на рис.1.10).
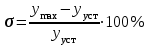 .
.




 Рис. 1.13
Рис. 1.13