Лекция по ОснАУ. лекции ОАУ часть1. Основы автоматического управления

• Название: Основы автоматического управления
• Анкор: Лекция по ОснАУ
• Дата: 05.10.2021
• Размер: 1.06 Mb.
• Имя файла: лекции ОАУ часть1.docx
• Тип: Документы; #241526
• страница: 7 из 9

4.6. Предельные соотношения логарифмических частотных характеристик. Влияние вариаций параметров на частотные характеристики соединений звеньев

Предельные соотношения ЛЧХ соединений звеньев. При построении ЛЧХ последовательного соединения типовых звеньев целесообразно предварительно определить особенности и некоторые параметры ЛЧХ и ФЧХ на низкой частоте (при ) и на высокой частоте (при  ). Сделать это можно по виду оператора W_P(s):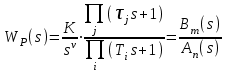

, (4.6)

где m и n – общие степени полиномов числителя и знаменателя ПФ W_P(s), включая интеграторы или дифференциаторы (при их наличии).

Сформулируем следующие правила.

На низкой частоте (при ):

• 
  Наклон ЛАХ составляет *(20дБ/дек),
  
• 
  Значение ФЧХ составляет *(/2)рад=*(90^о).
  

На высокой частоте (при  ):

• 
  Наклон ЛАХ составляет (nm)*(20дБ/дек)
  
• 
  Значение ФЧХ составляет (nm)*(/2)рад=(nm)*(90^о).
  

Знание и использование этих правил позволяет сразу наметить асимптотику ЛЧХ соединений типовых звеньев и уменьшить вероятность появления качественных ошибок при построении ЛЧХ.
Влияние вариаций параметров на ЛЧХ соединений звеньев. Рассмотрим по-отдельности влияние вариаций общего коэффициента передачи K и постоянных времени T_i или _j см. (4.2).
При изменении коэффициента передачи ЛАХ всего соединения будет подниматься при увеличении K или опускаться при его уменьшении. Величина L смещения ЛАХ при изменениии Kв K раз будет составлять L =20lgK (дБ). ФЧХ останется без изменений.

Все перечисленные выше в подразд. 4.6 правила останутся без изменений.

При изменении какой либо постоянной времени T_i или _j будет перемещаться влево или вправо соответствущая этой постоянной времени частота сопряжения. Это вызовет изменение вида обеих ЧХ. Все перечисленные выше в подразд.4.6 правила останутся без изменений. Кроме этого, не только наклон, но и местоположение низкочастотного участка асимптотической ЛАХ слева от _c,min останутся без изменений.

Все рассмотренные в подразд. 4.6 соотношения и правила следуют из
.ВЗАИМОСВЯЗЬ ЧАСТОТНЫХ И ВРЕМЕННЫХ ХАРАКТЕРИСТИК

СИСТЕМ УПРАВЛЕНИЯ

В разделе рассматривается следующий круг вопросов:

• 
  действие обратной связи на разных частотных диапазонах;
  
• 
  связь частотных характеристик разомкнутой и замкнутой СУ;
  
• 
  связь частотной полосы пропускания с быстродействием СУ.
  

Установление соответствия между характеристиками и показателями качества в частотной и временной областях позволяет более корректно решать задачи анализа и синтеза СУ.

5.1. Действие обратной связи в системах управления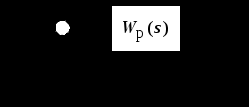





Рис. 5.1
Будем рассматривать СУ с типовой структурой, представленной на рис.5.1 (см. также подразд.2.5).

Для выяснения характера действия обратной связи на динамическую систему рассмот-рим сначала пример охвата пропорционального (то есть безынерци-онного) звена единичной отрицательной обратной связью. Положим W_Р(s)=K и определим передачу Ф(s) замкнутой системы при разных значениях K– табл.5.1.

Связь ПФ разомкнутой и замкнутой типовой СУ получена в подразд.2.6. Для случая безынерционного звена имеем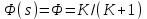

. (5.1)

Таблица 5.1

K	Ф	K/Ф*100(%)
1000	0.9991	105
100	0.991	104
10	0.9091	1100
1	0.5	200
0.1	0.091	10
0.01	0.00990.01K	1
0.001	0.000990.001K	0.1

Cуть приведенных в таблице значений заключается в следующем. Степень влияния обратной связи зависит от коэффициента передачи охватываемого звена. При больших коэффициентах изменение значительно. При K10 имеем Ф1. При малых коэффициентах передачи охватываемого звена характеристики разомкнутого и замкнутого звеньев отличаются незначительно, то есть обратная связь “не действует”. При K0.1 имеем ФK.

АЧХ некоторого динамического звена или всей СУ представляет собой зависимость коэффициента передачи от частоты. Поэтому обратная связь будет по-разному проявлять свое действие на разных частотах ЧХ.

Рассмотрим случай охвата единичной отрицательной обратной связью интегрирующего звена W_Р(s)=K/s. Используя (2.21), получим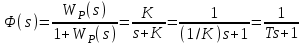

. (5.2)

Таким образом, в результате охвата интегратора обратной связью образуется апериодическое звено с единичным коэффициентом передачи (вне зависимости от K) и с постоянной времени T=1/K.

Н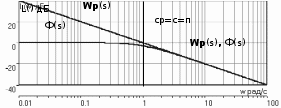
а рис.5.2 построены ЛАХ разомкнутой системы (в данном случае – интегрирующего звена с K=1) и замкнутой системы.

Рис.5.2

Из графиков видно, что при значительных усилениях в прямой цепи (L_Р()16 дБ) различия между ЛАХ разомкнутой и замкнутой системами велики и логарифмический модуль ЧХ замкнутой системы L()0 дБ (R()1). На высоких частотах, где L_Р()16 дБ, ЛАХ разомкнутой и замкнутой систем практически совпадают.

По АЧХ замкнутой системы определяют тот диапазон частот [0, _п], при котором R()1 и выходная координата y(t) “воспроизводит” входной управляющий сигнал f(t). Этот диапазон частот называется полосой пропускания системы. Правая граница этого диапазона – частота пропускания _п – обычно определяется из условия R(_п)=0.707R(0) (изменение модуля на –3 дБ).

Для рассматриваемого случая _п=_c=_ср, то есть совпадает с частотой сопряжения апериодического звена и частотой среза интегратора (см.подразд.3.2, 3.4).

Рассмотренное на данном примере действие обратной связи является закономерным для любых систем, образованных соединением различных звеньев. Это будет проиллюстрировано на примерах в подразд.5.3.

5.2. Полоса пропускания и быстродействие систем управления

Продолжим рассмотрение примера из подразд.5.1. Переходная характеристика апериодического звена является экспонентой со временем окончания процесса t_р=3T (см. подразд.1.4 и 3.4). В этом случае: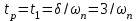

(с). (5.3)

В выражении (5.3) коэффициент  связывает быстродействие системы с ее частотной полосой пропускания; в данном случае =3.

Экспонента является апериодическим процессом; время первого согласования t₁, характеризующее быстродействие, и время регулирования t_р, т.е. время окончания процесса, совпадают подразд.1.4.

Таким образом, полоса пропускания _п и быстродействие системы находятся в обратно-пропорциональной зависимости – см.рис.5.3.

На рис.5.3,а показана АЧХ замкнутой системы при K=1 – кривая 1. Эта ЧХ соответствует апериодическому звену Ф(s)=1/(Ts+1), T=1c. В отличие от рассмотренных ранее ЧХ, в данном случае построены АЧХ не логарифмического модуля R(). При K=1 имеем _п=1рад/с.

На рис.5.3,б построена переходная характеристика замкнутой системы при K=1  кривая 1. Время процесса t_р1=3/_п1=3с.

Увеличим в два раза коэффициент передачи в прямом канале системы и положим его значение K=2. При этом ЛАХ L_Р() (прямая с наклоном, равным –20дБ/дек) поднимется вверх на 6 дБ, в результате получим _ср=_c=_п=2рад/с.

Рис. 5.3

Э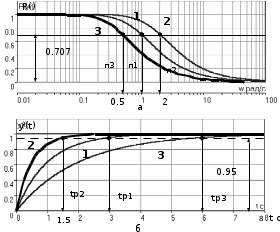
тому будет соответствовать кривая 2 на АЧХ (рис.5.3,а) с увеличенной в два раза полосой пропускания. Время переходного процесса наоборот уменьшится в два раза: t_р2=3/_п2=1.5с – кривая 2 на рис.5.3,б.

Уменьшим в два раза усиление в прямом канале системы, то есть положим K=0.5. При этом ЛАХ L_Р() опустится на 6дБ (относительно исходной ситуации при K=1) и _ср=_c=_п=0.5рад/с. Этому соответствует кривая 3 на АЧХ (рис.5.3,а) с уменьшенной в два раза полосой пропускания. Время переходного процесса наоборот увеличится в два раза: t_р3=3/_п3=6 с.

Заметим, что быстродействие системы мы изменяли не за счет варьирования какой-либо инерционности (постоянной времени). В исходной системе – рис.5.1, W_Р(s)=K/s  такого параметра вообще не присутствует. Полоса пропускания, а следовательно, и быстродействие, обеспечивались усилением в прямом канале системы. Так как рассматриваем СУ с единичной обратной связью, то это усиление совпадает с контурным усилением, то есть коэффициентом передачи контура обратной связи.

5.3. Примеры сопоставления частотных и временных характеристик

систем управления

Проверим выявленные выше закономерности на примерах СУ, рассмотренных в подразд.4.3 и 4.4, где описаны модели и подробно рассмотрен процесс построения ЛЧХ этих систем.

Астатическая система управления. Модель СУ приведена в подразд.4.3. Оператор W_Р(s) задан выражением (4.3). На рис.4.4 подробно отображены ЛЧХ и процесс их построения.

На рис.5.4 показаны ЛЧХ разомкнутой и замкнутой СУ.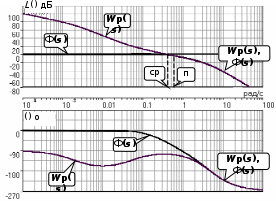


Рис. 5.4

В диапазоне частот, где усиления в разомкнутом контуре большие, ЧХ разомкнутой и замкнутой систем существенно различаются; модуль ЧХ замкнутой системы R()1 (L()0дБ). При L_р()0, ЧХ разомкнутой и замкнутой систем совпадают – обратная связь здесь “не работает”.

Частота среза разомкнутой системы _ср=0.4рад/с. Полоса пропускания замкнутой системы _п=0.54рад/с. Отметим, что для рассматриваемой системы частоты _ср и _п связаны соотношением:

_ср=0.74_п . (5.4)

_{Переходная характеристика приведена на рис.5.5. Заметим}, _{что время} окончания процесса t_р превосходит время первого согласования t₁ в пять раз.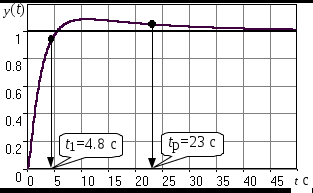





Рис. 5.5
Коэффициент связи быстро-действия и полосы пропускания: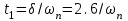

(с). (5.5)

Некоторое отклонение от значения =3 объясняется отличием вида процесса от экспоненты.

Статическая система управ-ления. Модель СУ приведена в подразд.4.4. Оператор W_Р(s) задан выражением (4.4). Рис.4.5 иллюстрирует процесс построения ЛЧХ системы.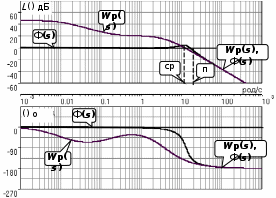


На рис.5.6 показаны ЛЧХ разомкнутой и замкнутой СУ.

Рис.5.6

В диапазоне частот, где усиления в разомкнутом контуре большие, ЧХ разомкнутой и замкнутой систем существенно различаются; модуль ЧХ замкнутой системы R()1 (L()0 дБ). На частотах, где L_Р()0, ЧХ разомкнутой и замкнутой систем совпадают – обратная связь здесь “не работает”. Частота среза разомкнутой системы _ср=12рад/с. Полоса пропускания замкнутой системы _п=18.5рад/с.

Переходная характеристика СУ приведена на рис.5.7. Заметим, что время окончания процесса t_р превосходит время первого согласования t₁ почти в 17раз! Это связано со значительной колебательностью, а также с “затягиванием” приближения координаты к установившемуся значению.

Оценим коэффициент  для этого процесса: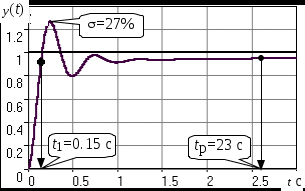




Рис. 5.7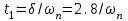
(с). (5.6)

Несмотря на отличие процесса от экспоненты, получили выражение, близкое к (5.3). Для этой системы

_ср=0.65_п . (5.7)

Таким образом, с достаточной достоверностью можно оценить быстродействие СУ по ее ЧХ, воспользовавшись соотношением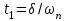

, (5.8)

где (2.53.3). Указанный для (5.8) диапазон значений  учитывает также и результаты расчета других СУ.

5.4. Синтез систем управления по требованиям к быстродействию

Выявленные в этом разделе зависимости между параметрами частотных и временных характеристик позволяют определить при синтезе контурное усиление для обеспечения требуемого быстродействия СУ.

Соотношение (5.6) позволяет найти необходимую полосу пропускания _п замкнутой СУ по времени первого согласования t₁.

Как будет показано в разд.7, для обеспечения “хорошего” переходного процесса типового вида с ограниченной колебательностью (см.подразд.1.4), ЛАЧХ синтезируемой разомкнутой системы также должна иметь типовой вид. В данном контексте это означает наличие достаточно длинного участка асимптотической ЛАХ с наклоном –20дБ/дек в окрестности частоты _ср. Именно такой типовой вид имеет ЧХ СУ, рассмотренной в подразд.4.3 и в подразд.5.3 (см.рис.4.4 и рис.5.4). С учетом (5.4), (5,7) и результатов расчета многих других СУ, можем с достаточной степенью приближения определить требуемую частоту среза разомкнутой синтезируемой системы

_ср (0.70.8)_п. (5.8)

Низкочастотный участок ЛАХ однозначно определит требуемое общее усиление.
6.ВЫНУЖДЕННЫЕ ДВИЖЕНИЯ В СИСТЕМАХ УПРАВЛЕНИЯ

В разделе рассматриваются вынужденные движения в СУ, которые проявляются после затухания свободной составляющей, т.е. после окончания переходного процесса. Рассматривается ряд типовых тестовых воздействий. Анализируется возможность отработки разных сигналов в зависимости от степени астатизма СУ. Определяются установившиеся ошибки, характеризующие точность работы СУ в установившемся режиме.

6.1. Типовые входные воздействия для систем управления.

Установившиеся движения в системах управления

Как уже говорилось в подразд.1.4, реакция любой СУ на входное воздействие определяется двумя составляющими: характеристиками входного воздействия и свойствами собственно самой СУ. Например, на рис.1.10 представлена реакция некоторой устойчивой СУ на постоянный сигнал (ступенчатое воздействие).

Можно выделить две составляющие реакции СУ на входной сигнал: переходный режим (переходный процесс) и установившийся режим. Решение линейного ДУ как раз содержит две составляющих – свободную и вынужденную – см.(2.8),подразд.2.3. Будем анализировать вынужденную составляющую, считая, что рассматриваемые здесь СУ  устойчивы.

Используем модель СУ типовой структуры – подразд.2.5, рис.2.3. В данном случае будем оперировать с ПФ Ф_e(s) по ошибке замкнутой системы, то есть используем модель, представленную на рис.2.4,б.

Будем считать, что ПФ прямого канала (то есть разомкнутой системы)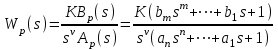

. (6.1)

Младшие коэффициенты полномов B_Р(s) и A_Р(s) равны единице; это означает, что усиление контура сосредоточено в одном параметре K.

Параметр   степень астатизма  определяется числом интеграторов в прямом канале СУ.

Рассмотрим три варианта СУ:

 = 0 – статическая система;

 = 1 – система с астатизмом 1-го порядка;

 = 2 – система с астатизмом 2-го порядка.

В подразд 2.6 получена связь ПФ замкнутой системы по ошибке через полиномы числителя и знаменателя ПФ разомкнутой системы  см.(2.24), (2.25). С учетом (6.1) получим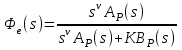

. (6.2)

Установившиеся режимы будем анализировать при так называемых типовых воздействиях, к которым предъявляются следующие требования:

• 
  воздействия должны быть адекватны реальным сигналам, подаваемым на СУ в процессе их функционирования;
  
• 
  воздействия должны иметь простое математическое описание.
  

Используем следующие типовые сигналы.

1. 
   Единичная -функция f(t)= (t), F(s)=1.
   
2. 
   Единичное ступенчатое воздействие f(t)= 1(t), F(s)=1/s.
   
3. 
   Линейно нарастающий сигнал, или – воздействие с постоянной скоростью f(t)= at, F(s)=a/s².
   
4. 
   Воздействие с постоянным ускорением f(t)= at²/2, F(s)=a/s³.
   

В соответствии с определением ПФ по ошибке (см.подразд.2.5)

E(s)=F(s) Ф_e(s). (6.3)

Вынужденное (установившееся) значение ошибки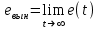

(6.4)

можно получить по теореме о конечном значении оригинала (2.13):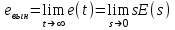

. (6.5)

Используя выражения (6.2)(6.5), можно определить, будет ли установившаяся ошибка нулевой, конечной либо будет стремится к бесконечности. Последнее будет означать, что СУ “не справляется” с входным воздействием.