Лекция по ОснАУ. лекции ОАУ часть1. Основы автоматического управления
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
|
2.5. Cистемы управления с типовой структурой На рис.2.1 представлена модель СУ в форме “вход-выход”. Известен оператор w преобразования входного воздействия в выходной сигнал, заданный в одной из рассмотренных выше форм представления. Информация о внутренней организации в такой модели отсутствует (модель системы со свернутой организацией). Рассмотрим модели с раскрытой внутренней организацией, которые отображают структуру СУ, то есть состав функциональных звеньев и связи между ними. Многообразие объектов и СУ порождает и большое множество структур, отличающихся числом и составом звеньев и способов их взаимосвязей. Здесь ограничимся так называемой типовой структурой СУ, реализующей принцип обратной связи – см.подразд.1.2, рис.1.2, а также п.1.3, рис.1.7. К моделям такого вида может быть приведено описание значительного множества СУ различного функционального назначения. Прежде всего вернемся к рассмотрению объекта управления приведенного на рис.1.2, где на объект воздействуют два внешних сигнала : сигнал управления µ(t) и сигнал возмущения fв(t).В зависимости от физической природы объекта возмущения действующие на него могут быть также разнообразными. Допустим, что y всех рассматриваемых объектах сигналы управления и сигналы возмущения взаимодействуют аддитивно, т. е. суммируются в некоторой точке. Также допустим, что известны математические операторы описывающие передачу сигналов к точке суммирования. Обозначим через W0(s) передаточную функцию прямого канала, т.е. передачу сигнала управления на выход объекта и через Wf (s) передаточную функцию объекта по возмущению. Тогда объект управления может быть представлен следующей структурой: 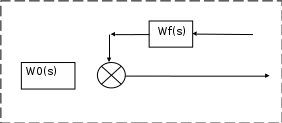   ОУ Fв(s)   M(s) Y(s)   где Fв(s),M(s), Y(s) изображения возмущающего сигнала, сигнала управления и выходного сигнала соответственно. С учетом принятой структуры ОУ типовая структура СУ с учетом возмущения приведена ниже 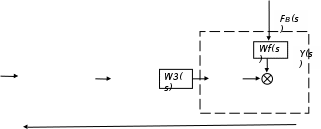  E(s)      W0(s) УМ ОУ    F(s) Р СП   W0(s)        - Прямой канал образован объектом управления ОУ и рядом звеньев, обеспечивающих реализацию управляющего воздействия (в данном случае это сервопривод СП и усилитель мощности УМ). Регулятор Р в соответствии с заложенным в него алгоритмом управления преобразует ошибку рассогласования в управляющее воздействие. В общем случае в зависимости от характеристик ОУ прямой канал может иметь разный состав последовательно соединенных функциональных звеньев. Очевидно, что в этом случае выходная координата СУ Y(s) и сигнал ошибки E(s) =F(s) – Y(s) включают две составляющих , одна из которых обусловлена сигналом управления, а вторая сигналом возмущения. В дальнейшем рассматривается только составляющая обусловленная сигналом управления, так как полученные результаты легко могут быть распространены и на сигнал возмущения. С учетом принятого ограничения структура преобразуется к виду на Рис.2.2  Рис.2.2 Операторы звеньев СУ будем задавать передаточными функциями (2.3) или (2.6). ПФ прямого канала без обратной связи, то есть ПФ разомкнутой СУ, будем обозначать Wр(s). ПФ последовательного соединения звеньев равна произведению ПФ отдельных звеньев, то есть 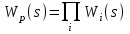 . (2.19) . (2.19) 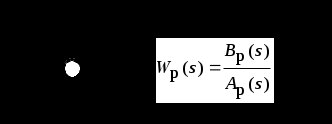 Рис.2.3 В результате типовая структура СУ может быть приведена к виду, представленному на рис.2.3. В данной модели фигурируют три координаты: входное воздействие f(t), выходной управляемый сигнал y(t) и сигнал ошибки e(t). Этой модели можно поставить в соответствие две модели типа “вход-выход” см.рис.2.4. 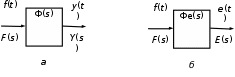 Рис.2.4 На рис.2.4,а представлена модель в виде ПФ Ф(s) замкнутой системы по управлению. На рис.2.4,б представлена модель в виде ПФ Фe(s) замкнутой системы по ошибке. 2.6. Связь передаточных функций замкнутой и разомкнутой типовой системы управления. Характеристический полином типовой системы управления Для СУ с типовой структурой (см. рис.2.3) выразим ПФ Ф(s) и Фe(s) замкнутой системы через оператор Wр(s) прямого канала, то есть системы без обратной связи. ПФ по управлению Ф(s)=Y(s)/F(s). Для получения этого оператора по модели, изображенной на рис.2.3, необходимо исключить координату E(s): Y(s)=E(s)Wр(s)=(F(s)Y(s))Wр(s). (2.20) Из (2.20) получаем 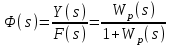 . (2.21) . (2.21)Выразим теперь ПФ замкнутой системы по управлению через полином числителя и знаменателя ПФ разомкнутой системы. Подставляя в (2.21) Wр(s)=Bр(s)/Aр(s), получим 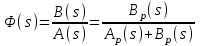 . (2.22) . (2.22)Таким образом, числители ПФ разомкнутой и ПФ по управлению замкнутой систем совпадают. Знаменатель ПФ замкнутой системы A(s), он же характеристический полином замкнутой системы равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы. ПФ по ошибке Фе(s)=E(s)/F(s). Для получения этого оператора по модели, изображенной на рис.2.3, необходимо исключить координату Y(s): E(s)= F(s)Y(s)=F(s)E(s)Wр(s). (2.23) Из соотношения (2.23) получаем 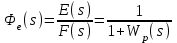 . (2.24) . (2.24)Выразим теперь ПФ замкнутой системы по ошибке через полином числителя и знаменателя ПФ разомкнутой системы. Подставляя в (2.24) Wр(s)=Bр(s)/Aр(s), получим 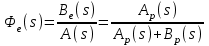 . (2.25) . (2.25)Таким образом, числитель ПФ замкнутой системы по ошибке совпал со знаменателем ПФ разомкнутой системы. Знаменатель ПФ замкнутой системы A(s), он же характеристический полином замкнутой системы, равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы, как и для ПФ по управлению. Сразу обобщим важную особенность. У любой СУ один характеристический полином; он не зависит от назначенных входа и выхода при получении конкретной ПФ. Соотношения (2.21), (2.22) и (2.24), (2.25) справедливы для рассматриваемой здесь типовой СУ, то есть для одноконтурной системы с единичной отрицательной обратной связью при отсутствии возмущения. 3. ТИПОВЫЕ ЗВЕНЬЯ СИСТЕМ УПРАВЛЕНИЯ В [1], [2], [3], [4] описаны различные СУ, объекты и функциональные элементы которых отличаются по назначению, физической природе сигналов, энергоемкости и по другим параметрам. Широкий класс функциональных элементов СУ с достаточной для процесса проектирования точностью может быть представлен так называемыми типовыми звеньями, представленными дифференциальными уравнениями первого и второго порядков. Из всех таких типовых звеньев рассмотрим ряд наиболее распространенных звеньев первого порядка, то есть описываемых дифференциальными уравнениями не выше первого порядка. Эти звенья ограничим следующим составом. Пропорциональное звено Интегрирующее звено (интегратор) Идеальное дифференцирующее звено (дифференциатор) Апериодическое звено первого порядка Пропорционально-дифференцирующее звено. Для описания процессов, содержащих колебательную составляющую, используется и также будет рассмотрено колебательное звено второго порядка. Операторы звеньев будем задавать дифференциальным уравнением и ПФ. Будем рассматривать переходную характеристику звена (реакцию на ступенчатое воздействие) и его частотные характеристики. 3.1. Пропорциональное звено Уравнение имеет следующий вид y = Kx. (3.1) Передаточная функция W(s) = K/1= K.(3.2) Описывающее это звено алгебраическое уравнение (3.1) можно рассматривать как вырожденное дифференциальное уравнение нулевого порядка. Во временной области это звено воспроизводит любой входной сигнал, изменяя его величину в K раз. В связи с этим такое звено называется также безынерционным. Единственный параметр K называется коэффициентом передачи. Получим частотный оператор звена: 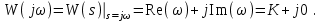 (3.3) (3.3)AЧХ пропорционального звена 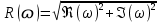 . (3.4) Модуль логарифмической ЧХ ЛАЧХ (размерность в децибеллах (дБ)) 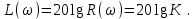 (3.5) (3.5)ФЧХ определяется выражением 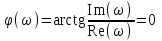 О. (3.6) О. (3.6)Рассмотрим АФХ, определяемую выражением (3.3) – см. рис.3.1.   Рис. 3.1 Мнимая составляющая ЧХ равна нулю, а вещественная часть равна K и не зависит от частоты. Поэтому траектория конца вектора ЧХ при изменении частоты от нуля до вырождается в точку. ЛЧХ определяются выражениями (3.4), (3.5), (3.6) и приведены на рис. 3.2. 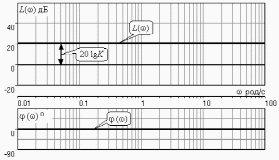 Рис. 3.2 часто также используют аббревиатуру “ЛАХ”) представляет собой прямую, параллельную оси частот и проходящую от этой оси на расстоянии 20lgK. Очевидно, что приведенная на рис.3.2 характеристика построена при значении K=10. ФЧХ от параметра K не зависит и совпадает с осью частот. При K=0 ЛАХ совпадает с осью частот (20lg1=0 дБ); для K1 ЛАХ будет проходить под осью частот. При изменении коэффициента передачи ЛАХ будет подниматься при увеличении K или опускаться при его уменьшении. Величина L смещения ЛАХ при изменениии Kв K раз будет составлять L =20lgK (дБ). Например, при увеличении K в 2 раза ЛАХ звена поднимется на 6 дБ, а при уменьшении в 2 раза опустится на такую же величину. 3.2. Интегрирующее звено (интегратор) Дифференциальное уравнение интегратора   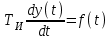 . (3.7) . (3.7)Передаточная функция представляется в двух видах: 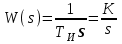 , (3.8) , (3.8)где K=1/TИ . Параметр TИ называется постоянной интегрирования, K коэффициент передачи или добротность интегратора. Далее будет использоваться запись ПФ интегратора в виде W(s)=K/s.  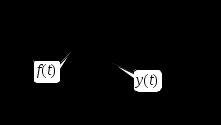 Рис. 3.3 Рис. 3.3Подадим на вход интегратора ступенчатое воздействие величины a, т.е. f(t)=a1(t). Изображение такой функции F(s)=a/s. Изображение сигнала на выходе интегратора Y(s)=F(s)W(s)=aK/s2. Обратное преобразование Лапласа дает реакцию интегратора на постоянный сигнал: y(t)= aKt см. рис.3.3. Таким образом, реакция интегратора на постоянное воздействие представляет собой линейно изменяющийся сигнал, тангенс угла наклона которого к оси времени пропорционален величине входного воздействия и коэффициенту передачи интегратора. Запишем частотный оператор интегрирующего звена: 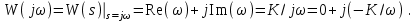 (3.9) (3.9)AЧХ ( модуль) 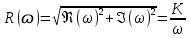 . (3.10) Модуль ЛАЧХ (дБ)   Рис. 3.4 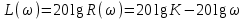 . (3.11) . (3.11)ФЧХ интегрирующего звена 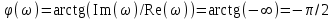 . (3.12) . (3.12)Рассмотрим АФХ, которая определяется выражением (3.9) – см. рис.3.4. Все точки АФХ располагаются на отрицательной части оси мнимых. На нулевой частоте интегратор имеет бесконечное усиление; при увеличении частоты модуль ЧХR() в соответствии с (3.10) монотонно уменьшается. Фазовый сдвиг на всех частотах составляет /2. Л 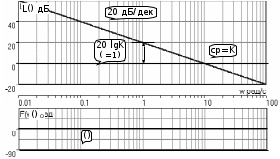 ЧХ интегратора строятся по формулам (3.10), (3.11), (3.12) – рис. 3.5. Рис. 3.5 ЛАХ представляет собой прямую, имеющую наклон –20дБ/дек; это означает, что при увеличении частоты в 10 раз модуль уменьшается также в 10 раз. Действительно, определим изменение модуля на десятикратном интервале изменения частоты в любом месте частотного диапазона: L=L(10i) L(i) = 20lgR(10i) 20 lgR(i)= = (20 lgK 20 lg(10) 20lg(i)) (20 lgK 20 lg(i))= –20дБ . Для определения местоположения ЛАХ найдем точку её пересечения с осью частот. Данная точка называется частотой среза; при этом имеем R(ср)=1, а L(ср)=0дБ. Из (3.10) видно, что R()=1 при =K. Проведенная через эту точку прямая линия с наклоном –20дБ/дек и является ЛАХ интегратора с коэффициентом передачи K. Найдем еще одну характерную точку при =1. Из (3.11) следует, что на данной частоте 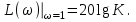 Прямая, проведенная через эту точку и через точку на оси частот =K будет иметь наклон –20дБ/дек. Заметим, что для интегратора с K =1 обе характерные точки совпадают (ср=1). Прямая, проведенная через эту точку и через точку на оси частот =K будет иметь наклон –20дБ/дек. Заметим, что для интегратора с K =1 обе характерные точки совпадают (ср=1).ФЧХ интегрирующего звена, как следует из (3.12), представляет собой прямую линию, параллельную оси частот – см. рис.3.5. При изменении коэффициента передачи (единственного параметра интегратора) ЛАХ будет смещаться параллельно самой себе: подниматься при увеличении K или опускаться при уменьшении K. Величина смещения ЛАХ L при изменениии Kв K раз будет составлять L = 20lg(K) дБ. Например, при увеличении K в 10 раз ЛАХ поднимется на 20 дБ, а при уменьшении K в 4 раза опуститься на 12 дБ. |
