Лекция по ОснАУ. лекции ОАУ часть1. Основы автоматического управления

• Название: Основы автоматического управления
• Анкор: Лекция по ОснАУ
• Дата: 05.10.2021
• Размер: 1.06 Mb.
• Имя файла: лекции ОАУ часть1.docx
• Тип: Документы; #241526
• страница: 6 из 9

3.7. Неминимально-фазовые звенья

Рассмотренные выше в этом разделе типовые звенья имеют полюсы (корни полинома знаменателя ПФ) или нули (корни полинома числителя ПФ), которые либо принадлежат левой полуплоскости комплексной плоскости корней, либо равны нулю, как в случае интегрирующего и идеального дифференцирующего звеньев. ПФ, имеющие такие полюсы и нули, называются минимально-фазовыми. Эти ПФ имеют наименьшие по модулю фазовые сдвиги по сравнению с такими передаточными функциями, которые содержат нули и/или полюсы справа от мнимой оси.

Звенья, содержащие правые полюсы или нули, называются неминимально-фазовыми [2], [3], [4], [6], [7]. Например, звено первого порядка с ПФ W(s)=K/(Ts1) имеет правый полюс s=1/T и расходящийся переходный процесс, как это будет видно, если получить его с использованием (3.21), (3.22). Такое звено называется неустойчивым апериодическим звеном 1-го порядка. Если провести выкладки, аналогичные приведенным в выражениях (3.23) – (3.27), то будет видно, что неустойчивое апериодическое звено имеет одинаковую АЧХ с рассмотренным в подразд.3.4 устойчивым апериодическим звеном W(s)=K/(Ts+1), а фазовый сдвиг определяется соотношением ()=+arctg (T) – см.рис.3.16.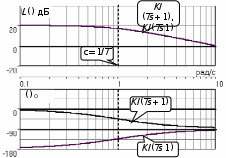


Рис. 3.16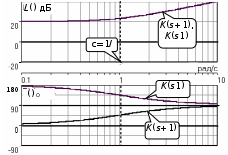


Звено с ПФ W(s)=K(s1) отличается от рассмотренного выше пропорционально-дифференцирующего звена наличием правого нуля s=1/. Соответствующие этому звену ЧХ приведены на рис.3.17.

Рис. 3.17

Если сделать выкладки, соответствующие выражениям (3.32) – (3.35) для этого звена, то как и в предыдущем случае получим совпадающую со звеном W(s)=K(s+1) АЧХ, а фазовый сдвиг будет определяться выражением ()=arctg() – см.рис.3.17.
4.ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК СОЕДИНЕНИЙ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ УПРАВЛЕНИЯ

Для анализа и синтеза СУ широко используются частотные характеристики. Частотная область обладает высокой информативностью в плане выявления зависимости свойств и показателей качества СУ от операторов отдельных звеньев и значений их параметров.

В подразд.2.5 приведена типовая структура одноконтурной СУ с единичной отрицательной обратной связью. Будем считать, что прямой канал передачи управляющего воздействия образован последовательным соединением типовых звеньев, рассмотренных в разд.3. Ряд важных свойств замкнутых СУ может быть выявлен при анализе и сформирован при синтезе по частотным характеристикам разомкнутых систем, то есть по оператору прямого канала без обратной связи.

Целью раздела является описание процесса построения ЧХ СУ без использования компьютера, так как это позволяет установить влияние оператора каждого звена на вид ЧХ и, в конечном счете, на свойства СУ.

4.1. Логарифмические частотные характеристики последовательного соединения типовых звеньев

Рассмотрим последовательное соединение нескольких звеньев, операторы которых заданы передаточными функциями. Как сказано в подразд.2.5, ПФ такого соединения равна произведению ПФ звеньев.

Построение логарифмических ЧХ соединения основано на следующих двух положениях.

1. 
   Используется то обстоятельство, что логарифм произведения равен сумме логарифмов сомножителей. С учетом того, что ПФ звеньев являются комплексными дробно-рациональными функциями, отдельно ЛАЧХ разомкнутой системы есть сумма ЛАЧХ звеньев соединения; ЛФЧХ разомкнутой системы также есть сумма ЛФЧХ отдельных звеньев.
   
2. 
   По асимптотическим ЛАХ отдельных звеньев может быть построена асимптотическая ЛАХ системы, а уточненная ЛАХ системы может быть получена путем учета поправок. При этом необходимо заметить, что в зависимости от решаемой задачи учет всех поправок может и не понадобится.
   

Построим частотные характеристики СУ, структурная схема которой представлена на рис.4.1.

Р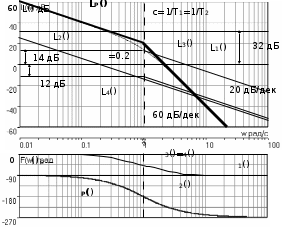
ис.4.1

Прямой канал передачи управляющего воздействия представляет собой последовательное соединение типовых звеньев: пропорциональное W₁(s)=K₁=40, интегрирующее W₂(s)=K₂/s=0.2/s, два апериодических звена W₃(s)=K₃/(T₁s+1)=5/(s+1), W₄(s)=K₄/(T₂s+1)=0.25/(s+1). В данном случае апериодические звенья имеют совпадающие постоянные времени T₁=T₂=1с.

Построение ЛАХ. На рис.4.2. построены асимптотические ЛАХ L_i(), i=1,2,3,4 отдельно каждого звена, а также ЛАХ L_р() последовательного соединения.

Рис. 4.2

ЛАХ пропорционального звена L₁() проходит параллельно оси частот на расстоянии 20lgK_1=20lg40=20lg(10*2*2)=20дБ+6дБ+6дБ=32дБ.

ЛАХ интегратора L₂() представляет собой прямую с наклоном 20дБ/дек, которая пересекает ось частот при =0.2 рад/с.

Асимптотическая ЛАХ L₃() апериодического звена с ПФ W₃(s)слева от частоты сопряжения 1/T₁=1 рад/с проходит параллельно оси частот на расстоянии 20lgK_3=20lg5=20lg(10/2)=20lg1020lg2=20дБ6дБ=14дБ; справа от линии сопряжения имеет наклон 20дБ/дек.

Асимптотическая ЛАХ L₄() апериодического звена с ПФ W₄(s)слева от частоты _с=1/T₂=1 рад/с проходит параллельно оси частот на расстоянии20lgK_4=20lg(0.25)=20lg((1/2)*(1/2))=(6дБ)+(6дБ)=12дБ; справа от линии сопряжения имеет наклон 20дБ/дек.

Сумма этих четырех асимптотических ЛАХ L_P() представляет собой асимптотическую ЛАХ разомкнутой системы, то есть ЛАХ последо-вательного соединения всех звеньев прямого канала. На рис.4.2 приведена и уточненная ЛАХ L_P() (тонкая линия). Максимальное значение поправки L(_с)=2*(3дБ)=6дБ.

Построение ФЧХ. Для пропорционального звена ₁()=0 во всем диапазоне частот.

ФЧХ интегрирующего звена ₂()=/2 во всем диапазоне частот.

ФЧХ обоих апериодических звеньев совпадают и имеют значение /4 на частоте сопряжения _c=1/T_1=1/T_2=1рад/с.

Результирующая ФЧХ _P() для рассматриваемого примера представляет собой смещенную на /2 удвоенную характеристику апериодического звена с _c=1рад/с. На частоте сопряжения в данном случае имеем фазовый сдвиг _P(_c)=( /2)+2*(/4)= .

4.2. Алгоритм построения логарифмической амплитудной характеристики последовательного соединения типовых звеньев

Как следует из разд.3 и подразд.4.1, построение асимптотической ЛАХ последовательного соединения типовых звеньев сводится к суммированию на графике отрезков прямых линий с наклонами, кратными 20дБ/дек.

Используем более эффективный способ построения ЛАХ последо-вательного соединения звеньев, который не требует построения ЛАХ отдельно каждого звена и последующего суммирования этих ЛАХ.

Для рассмотренного в подразд.4.1. примера представим ПФ W_P(s)=W₁(s)W₂(s)W₃(s)W₄(s) в следующем виде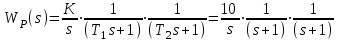

. (4.1)

Основным в данном случае является то обстоятельство, что коэффициенты передач всех звеньев сосредоточены в одном (первом) сомножителе 10/s; оба апериодических звена имеют единичный коэффициент передачи. Очевидно, что результирующая ЛАХ от такого перераспределения параметров должна остаться без изменений.

П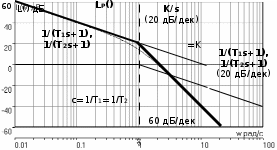
остроим ЛАХ звеньев-сомножителей из (4.1) – см.рис.4.3.

Рис. 4.3

Проведем вертикальную штриховую линию сопряжения на частоте _c=1/T_1=1/T_2=1рад/с. Заметим, что частоты сопряжения позволяют оцифровать ось частот.

Построим ЛАХ первого сомножителя в (4.1). Этот сомножитель соответствует интегрирующему звену с коэффициентом передачи K=10; его ЛАХ представляет собой прямую с наклоном 20дБ/дек, пересекающую ось частот при =10. От левой границы частотного диапазона до частоты сопряжения _c этот участок ЛАХ проведем сплошной линией, а справа от _c до =K=10 наметим ее штрихами – см.рис.4.3.

Теперь построим ЛАХ звеньев 1/(s+1). Слева от _c асимптотическая ЛАХ этих звеньев проходит по оси частот, так как 20lg(1)=0 дБ.

Очевидно, что характеристики апериодических звеньев с K=1 не изменят при суммировании построенную ранее характеристику интегратора на диапазоне _c. На диапазоне частот _c сформировавшийся наклон 20дБ/дек будет изменен на 2*(20)дБ/дек. Продолжение вправо от _c прямой с наклоном 60дБ/дек образует результирующую асимптотическую ЛАХ всего соединения звеньев – см.рис.4.3.

Сформируем алгоритм построения ЛАХ последовательного соединения любых типовых звеньев, позволяющий получить характеристику без предварительного построения и суммирования ЛАХ отдельных звеньев.

1. 
   Оператор последовательного соединения звеньев приводится к виду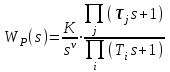
   

, (4.2)

=…2,1,0,1,2,… .

Первый сомножитель в (4.2) определит наклон низкочастотного участка ЛАХ (слева от крайней левой линии сопряжения).

При =0 имеем “статическую систему”; наклон низкочастотного участка ЛАХ будет равен 0дБ/дек  ЛАХ пройдет параллельно оси частот.

При =1 имеем “систему с астатизмом первого порядка”; наклон низкочастотного участка ЛАХ будет равен 20дБ/дек.

При =2 имеем “систему с астатизмом второго порядка”; наклон низкочастотного участка ЛАХ будет равен 40дБ/дек.

Значения =1 или=2 соответствуют наличию в соединении одного или двух идеальных дифференцирующих звеньев; наклон низкочастотного участка ЛАХ будет равен +20дБ/дек или +40дБ/дек.

2. 
   На частотной оси помечаются частоты сопряжения; при этом оцифровывается вся шкала частот. Проводятся вертикальные штриховые линии сопряжения. Каждая линия помечается в соответствии со своей постоянной времени 1/T_i или 1/_j. Важным фактором является четкое разграничение, принадлежит линия сопряжения постоянной времени T_i знаменателя, или постоянной времени _j числителя ПФ.
   
3. 
   Для диапазона частот _c,min , то есть левее самой левой линии сопряжения, строится ЛАХ сомножителя (K/s^).
   
4. 
   Далее построение результирующей ЛАХ производится от _c,min вправо, т.е. в сторону увеличения частоты. Пересечение ранее сформированного участка ЛАХ с очередной линией сопряжения изменяет наклон ЛАХ на 20дБ/дек, если линия сопряжения помечена 1/T_i, или на +20дБ/дек, если линия сопряжения помечена 1/_j. Необходимо иметь ввиду, что постоянные времени некоторых звеньев могут совпадать, как это имеет место в рассмотренном примере подразд.4.1 и 4.2. В этом случае изменение наклона асимптотической ЛАХ будет иметь величину, кратную 20дБ/дек.
   

Описанный способ в значительно меньшей степени подвержен возникновению ошибок при построении ЛАХ по сравнению со способом, основанном на построении ЛАХ отдельно каждого звена с последующим суммированием характеристик. Единственным требованием для получения достоверной результирующей ЛАХ является точное соблюдение кратным 20дБ/дек величин наклонов отрезков асимптотической характеристики.

4.3. Пример построения логарифмических частотных характеристик астатической системы управления

Рассмотрим подробно процесс построения ЛЧХ по предложенному в подразд.4.2 алгоритму для СУ, имеющей ПФ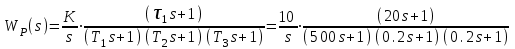

. (4.3)

Построение ЧХ отображено на рис.4.4. Проводим линии сопряжения на частотах _c1=1/T_1=0.002 рад/с, _c2=1/_1=0.05 рад/с, _c3=1/T_2=1/T_3=5 рад/с и помечаем их. На шкале частот эти значения отмечены треугольными метками – острием вверх на частоте, равной значению нуля 1/₁, и острием вниз на частотах, равных значениям полюсов 1/T_i. Направление метки показывает, в какую сторону происходит “излом” асимптотической ЛАХ.

Для диапазона частот _c,min = _c1=1/T_1=0.002рад/с строим участок ЛАХ, соответствующий сомножителю 10/s. Слева от _c1 сразу проводим сплошную линию; ее продолжение штриховой линией до _=10рад/с используется только для построения ЛАХ интегратора.

Р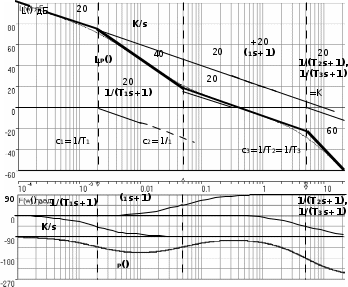
ис.4.4

Частота _c1 “помечена полюсом”, поэтому справа от нее (то есть в сторону увеличения частоты) наклон изменится на 20дБ/дек и будет составлять 40дБ/дек. Прямую с таким наклоном следует провести до _c2.

Частота _c2 “помечена нулем”, поэтому справа от нее наклон изменится на +20дБ/дек и будет составлять 20дБ/дек. Этот наклон следует сохранить до _c3.

Частота _c3 помечена сразу двумя полюсами; справа от нее наклон измениться на 2*(20дБ/дек) и будет составлять 60дБ/дек. Этот наклон останется неизменным при .

На рис.4.4 показаны ЛАХ звеньев 1/(T_is+1) и 1/(_js+1). Видно, что каждое такое звено имеет модуль 0 дБ слева от своей частоты сопряжения; прибавление его характеристики на _c не изменяет ранее сформированного участка ЛАХ соединения. Справа от своей частоты сопряжения такое звено “срабатывает”, изменяя наклон асимптотической ЛАХ соединения.

ФЧХ _P() формируется путем построения ФЧХ отдельных звеньев и последующего их суммирования – см.рис.4.4.

4.4. Пример построения логарифмических частотных характеристик статической системы управления

Проведем построение ЛЧХ для статической СУ, имеющей ПФ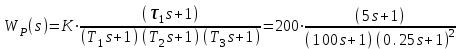

. (4.4)

П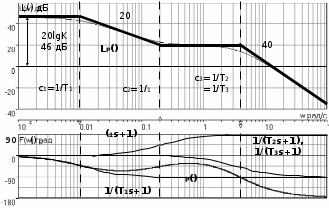
остроение ЧХ отображено на рис.4.5. После оцифровки оси частот и нанесения на сетку ЛАХ вертикальных штриховых линий сопряжения начинается построение собственно ЛАХ L_P(). Слева от минимальной частоты сопряжения _c,min=_c1=1/T_1=0.01рад/с, определяемой самой большой постоянной времени в СУ, формируем низкочастотный участок ЛАХ. В данном случае это прямая, параллельная оси частот и проходящая на расстоянии20lg200=20lg(10*10*2)=20lg10+20lg10+20lg2= =20дБ+20дБ+6дБ=46дБ.

Рис.4.5

Линия сопряжения _c1 соответствует полюсу 1/T₁. Поэтому переход через нее асимптотической ЛАХ в сторону увеличения частоты сопровождается изменением наклона на –20дБ/дек. Прямую с таким наклоном проводим до следующей частоты сопряжения _c2=0.2рад/с, которая соответствует нулю 1/₁, и переход через нее асимптотической ЛАХ в сторону увеличения частоты сопровождается изменением наклона на +20дБ/дек. В результате суммарный наклон следующего участка ЛАХ будет составлять 0дБ/дек; параллельный оси частот участок ЛАХ следует продолжить до частоты сопряжения _c3=4рад/с. На линии сопряжения этой частоты “срабатывают” два полюса, так как “включаются” два апериодических звена с одинаковыми постоянными времени. Переход через эту линию сопровождается изменением наклона на 2*(20дБ/дек)=40дБ/дек. В результате окончательный наклон ЛАХ справа от _c3=4рад/с равен 40дБ/дек.

ФЧХ _P() формируется путем построения ФЧХ отдельных звеньев и последующего их суммирования – см.рис.4.5.

4.5. Пример построения логарифмических частотных характеристик реального дифференцирующего звена

Идеальное дифференцирующее звено (см.подразд.3.3) имеет равномерно возрастающий модуль R() во всем диапазоне частот [0,); при , модуль R(). Такая идеальная модель звена может соответствовать реальности только в ограниченном диапазоне частот. В связи с этим часто используют так называемое реальное дифференцирующее звено, у которого, начиная с некоторой частоты, рост модуля R() ограничивается. ПФ такого звена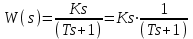

(4.5)

можно рассматривать как ПФ последовательного соединения двух ранее рассмотренных типовых звеньев – идеального дифференцирующего и апериодического первого порядка (4.5).

На рис.4.6 представлено построение ЛАХ реального дифферен-цирующего звена с K=0.1 и T=0.25с.

Р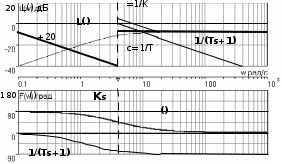
ис.4.6

Единственная частота сопряжения _c=1/T=4рад/с определяется апе-риодическим звеном 1/(Ts+1)=1/(0.25s+1).

До частоты сопряжения _c=1/T наклон ЛАХ определяется наличием дифференциатора и составляет +20 дБ/дек; этот участок ЛАХ (в данном случае – его продолжение за _c) пересечет ось частот при =1/K=10рад/с. На частоте _c “включается” асимптотическая ЛАХ апериодического звена, изменяя имеющийся слева от _c наклон на 20дБ/дек. В результате получаем суммарный наклон ЛАХ справа от частоты сопряжения, равный 0дБ/дек и при [_c,) ЛАХ будет параллелен оси частот.

Результирующая ФЧХ () представляет собой ФЧХ апериодического звена, смещенную на +/2, так как такой фазовый сдвиг вносит идеальное дифференцирующее звено во всем диапазоне частот – см.рис.4.6.