Лекция по ОснАУ. лекции ОАУ часть1. Основы автоматического управления
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
|
6.2. Расчет установившихся ошибок СтатическаяСУ. В прямом канале системы отсутствуют интегрирующие звенья, т.е. =0. В этом случае (6.2) приводится к виду: 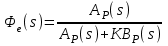 . (6.6) . (6.6)С использованием (6.6) будем находить вынужденные ошибки при разных входных воздействиях. -функция f(t)= (t). 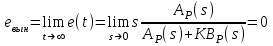 . (6.7) . (6.7)Результат получен с учетом (6.1), где раскрыта запись полиномов BР(s)и AР(s). Ступенчатое воздействие f(t)= 1(t). 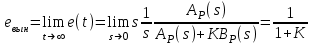 . (6.8) . (6.8)Линейное воздействие f(t)= at. 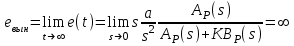 . (6.9) . (6.9)Из (6.9) видно, что аналогичный результат будет получен и при параболическом воздействии, изображение которого F(s)=a/s3. Система с астатизмом первого порядка. В прямом канале системы присутствует одно интегрирующее звено, т.е. = 1. В этом случае (6.2) приводится к виду: 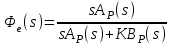 . (6.10) . (6.10)С использованием (6.10) также определим вынужденные ошибки. -функция ( функция Дирака ) f(t)= (t). 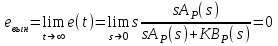 . (6.11) . (6.11)Ступенчатое воздействие f(t)= 1(t). 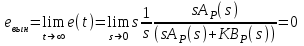 . (6.12) . (6.12)Линейное воздействие f(t)= at. 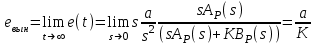 . (6.13) . (6.13)Воздействие с постоянным ускорением f(t)= at2/2. 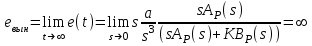 . (6.14) . (6.14)Система с астатизмом второго порядка. В прямом канале системы присутствуют два интегрирующих звена, т.е. = 2. В этом случае (6.2) приводится к виду: 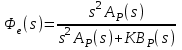 . (6.15) . (6.15)С использованием (6.15) также определим вынужденные ошибки при разных входных воздействиях. -функция f(t)= (t). 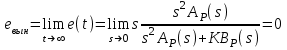 . (6.16) . (6.16)Ступенчатое воздействие f(t)= 1(t). 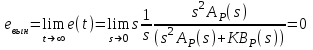 . (6.17) . (6.17)Линейное воздействие f(t)= at. 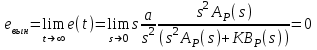 . (6.18) . (6.18)Воздействие с постоянным ускорением f(t)= at2/2. 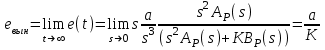 . (6.19) . (6.19)6.3. Анализ соответствия астатизма системы управления и ее функционального назначения  Таблица 6.1
Обобщим полученные выше результаты. Cведем вычисленные по (6.7)(6.9), (6.11)(6.14) и (6.16)(6.19) ошибки в табл. 6.1. Для наглядности аналогичная таблица с изображениями процессов приведена на рис.6.1. Р 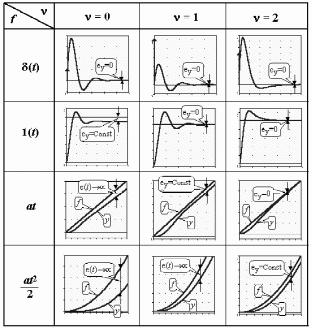 ис.6.1 Рассмотрим верхнюю строку таблиц. Статическая и, тем более, астатические системы “отрабатывают” -функцию с нулевой установившейся ошибкой (при t, f(t)=y(t)=0). Вторая строка таблиц соответствует подаче на вход ступенчатого воздействия, то есть постоянного сигнала. Статическая система отрабатывает его с конечной ошибкой, определяемой усилением в контуре. Астатические системы справляются с этим сигналом с нулевой установившейся ошибкой. Третья строка показывает реакции систем уже на меняющийся сигнал, в данном случае с постоянной скоростью. Статическая система с таким сигналом не справляется – выходная координата не может “следить” за таким сигналом, рассогласование будет накапливаться. Система с астатизмом 1-го порядка имеет конечную установившуюся ошибку, прямо пропорциональную скорости изменения входного сигнала и обратно-пропорциональную контурному усилению. Система с астатизмом 2-го порядка справляется с таким сигналом с нулевой установившейся ошибкой. Последняя строка таблиц показывает реакции систем на наиболее “сложный” из приведенных входных сигналов – с изменяющейся скоростью (но с постоянным ускорением). С таким сигналом справляется только система с астатизмом 2-го порядка, с конечной ошибкой, прямо пропорциональной ускорению изменения входного сигнала и обратно-пропорциональной усилению в контуре. 6.4. Синтез систем управления по требованиям к установившимся процессам Реакция СУ на входное воздействие содержит две составляющих – переходный процесс и вынужденный режим. В соответствии с этим и решение линейного дифференциального уравнения также содержит две составляющих – см. (2.8), подразд. 2.3. Обеспечение качества СУ может быть разделено на два этапа: синтез вынужденных режимов (установившихся процессов) и синтез переходных процессов, причем в указанной последовательности. Синтез вынужденных режимов и синтез переходных процессов может быть осуществлен разными мерами – см. подразд.7.3. Второй этап, т.е. синтез динамики системы, можно и необходимо осуществлять таким образом, чтобы не ухудшить обеспеченное на первом этапе качество установившегося режима. Обеспечение возможности отработки системой управления входного воздействия. Для того, чтобы СУ смогла “справиться” с входным воздействием определенного типа, установим соответствие степени астатизма характеристикам этого воздействия – см.табл.6.1, подразд.6.3. Для систем стабилизации, которые должны поддерживать выходную координату с заданной конечной ошибкой при постоянном входном воздействии, могут быть использованы статические СУ. Для следящих систем, которые должны воспроизводить (отслеживать) меняющиеся во времени входные сигналы, необходимо использовать астатические СУ. Порядок астатизма определяется характеристиками (“сложностью”) входных сигналов. Астатизм определенного порядка в СУ может также потребоваться для обеспечения нулевой установившейся ошибки. Например, для СУ, которая по функциональному назначению является системой стабилизации, для получения eуст=0 при постоянном входном сигнале необходимо обеспечить =1. Также для следящей СУ при отработке сигналов с постоянной скоростью необходимо иметь =2 в случае требования eуст=0. Обеспечение необходимого контурного усиления в системе управления. Для тех случаев, когда задана требуемая (допустимая) конечная установившаяся ошибка, может и должно быть определено необходимое усиление в контуре обратной связи – см.табл.6.1, подразд.6.3. Для статической системы необходимый коэффициент контурного усиления  (6.20) (6.20)В (6.20) eуст,тр требуемая (допустимая) установившаяся ошибка. Для СУ с астатизмом 1-го и 2-го порядков необходимый коэффициент контурного усиления определяется из соотношения 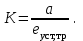 (6.21) (6.21)В (6.21) a скорость линейного воздействия для системы с астатизмом 1-го порядка или ускорение параболического воздействия для системы с астатизмом 2-го порядка. Отметим, что нулевые установившиеся ошибки определяются наличием интеграторов и не зависят от усиления в контуре обратной связи или от других параметров системы. В таких случаях контурное усиление конкретизируется, исходя из других требований, например, необходимого быстродействия – см.подразд.5.4. 7.УСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ В разделе исследуется устойчивость замкнутых СУ. Рассматриваются алгебраические и часто тные критерии устойчивости. Вводятся оценки запасов устойчивости. Формируется типовая частотная характеристика, соответствующая типовому поведению СУ. Описан “частотный” синтез звена коррекции для обеспечения достаточных запасов устойчивости и типового поведения СУ. 7.1. Характеристический полином замкнутой системы управления. Алгебраические критерии устойчивости В подразд.1.4 вводится понятие устойчивых объектов и СУ с позиции их поведения. Показано, что устойчивость является необходимым условием функционирования СУ. В подразд.2.3 понятие устойчивости связывается в решением ДУ, которое описывает поведение СУ. Там же сформулированы необходимое и достаточное условия устойчивости, а именно: для устойчивости СУ необходимо и достаточно, чтобы корни характеристического полинома принадлежали левой полуплоскости плоскости корней. Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой. 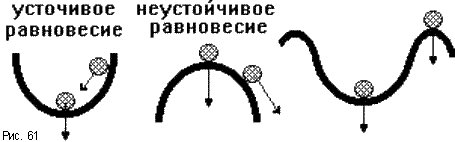 Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы. Говорят, что система устойчива "в малом", если определен факт наличия устойчивости, но не определены ее границы. Система устойчива "в большом", когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы. В соответствии с классическим методом решение дифференциального уравнения ищется в виде: y(t) = yвын(t) + yсв(t). Здесь yсв(t) - общее решение однородного дифференциального уравнения, то есть уравнения с нулевой правой частью: 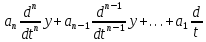 y + y + 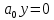 Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. yвын(t) - частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие f(t). Поэтому вторая составляющая общего решения называется вынужденный. Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса. М 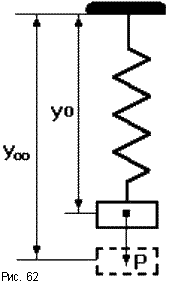 ожно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением. Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р. После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей yвын = y(t ). Если внешнее воздействие само будет изменяться по синусоидальному закону P = Posin( t + ), то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то есть yвын = ymaxsin( t + y). ожно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением. Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р. После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей yвын = y(t ). Если внешнее воздействие само будет изменяться по синусоидальному закону P = Posin( t + ), то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то есть yвын = ymaxsin( t + y).Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t . Свободная составляющая представляет собой сумму из n отдельных составляющих: yсв(t)= 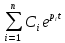 , ,где piкорни характеристического уравненияAn(p)=anpn+ an -1 pn -1+ . . . a1p + a0 = 0 , . Корни могут быть либо вещественными pi = αi, либо попарно комплексно сопряженными pi = αi ± j i. Постоянные интегрирования Ci определяются исходя из начальных и конечных условий, подставляя в общее решение з 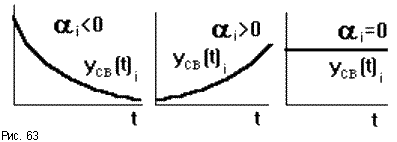 начения u, y и их производные в моменты времени t = 0 и t . начения u, y и их производные в моменты времени t = 0 и t .Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая yсв(t)i, каждому положительному - экспоненциально расходящаяся, каждому нулевому корню соответствует yсв(t)i = const (рис.63). Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой i, при положительной вещественной части - расходящиеся колебания, при нулевой - незатухающие (рис.64). 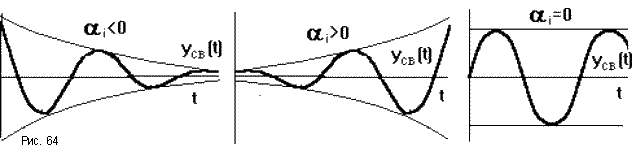 Так как после снятия возмущения yвын(t) = 0, то устойчивость системы определяется только характером свободной составляющей yсв(t). zПоэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанному в отклонениях, должна с 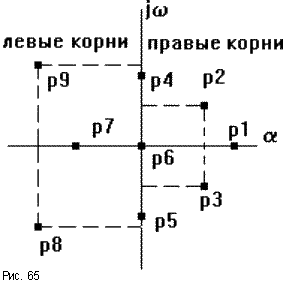 тремиться к нулю, то есть затухать. тремиться к нулю, то есть затухать.Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называются левыми, с положительными - правыми (рис.65). Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где an = 0), а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости. Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости. Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и частотные (основаны на исследовании частотных характеристик). Для СУ, построенных по принципу обратной связи, устойчивость определяет характеристический полином замкнутой СУ. Если модель типовой СУ задана структурной схемой (подразд.2.5, рис.2.2), то по ПФ звеньев прямого канала легко определяется оператор WР(s) и структура СУ приводится к виду, изображенному на рис.2.3. В подразд.2.6 определяются ПФ по управлению и по ощибке замкнутой СУ через оператор WР(s) разомкнутой системы. В обоих случаях ПФ замкнутой системы имеют одинаковый знаменатель – характеристический полином. С учетом обозначений WР(s)=BР(s)/AР(s), характеристический полином A(s) замкнутой системы определяется выражением: 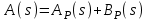 . (7.1) . (7.1)Таким образом, характеристический полином замкнутой системы равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы. Принадлежность корней характеристического полинома левой части комплексной плоскости можно определить непосредственным вычислением корней. Также могут быть использованы критерии устойчивости. Алгебраические критерии устойчивости позволяют установить факт принадлежности корней полинома левой полуплоскости по соотношениям коэффициентов ai полинома 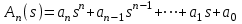 . . |
