Лекция по ОснАУ. лекции ОАУ часть1. Основы автоматического управления

• Название: Основы автоматического управления
• Анкор: Лекция по ОснАУ
• Дата: 05.10.2021
• Размер: 1.06 Mb.
• Имя файла: лекции ОАУ часть1.docx
• Тип: Документы; #241526
• страница: 9 из 9

Критерий устойчивости Гурвица.

Итак, пусть характеристический полином звена или системы автоматического регулирования имеет вид: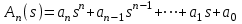

.

Для устойчивости необходимо и достаточно, чтобы при a_n>0 все диагональные определители матрицы Гурвица были положительными. Матрица записывается следующим образом: по главной диагонали ставятся все коэффициенты начиная с a_n-1, затем каждая строка дополняется по правилу четности, на место отсутствующих коэффициентов ставятся нули.

Тогда матрица имеет вид: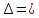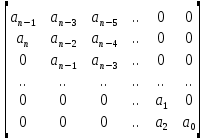


Это квадратная матрица (n*n). Ее диагональным определителями являются: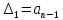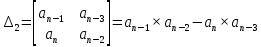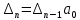





…………………………………………


Необходимым (но не достаточным) условием устойчивости является требование, чтобы все коэффициенты a_i,i=0,…,n, были положительные. Если хотя бы один коэффициент полином, отрицательный то это уже является достаточным условием принадлежности одного или нескольких корней правой полуплоскости.

Для полинома первого порядка A₁(s)=a₁s+a₀ приведенное условие устойчивости является не только необходимым, но и достаточным, так как единственный действительный корень s_1=a₀/a₁.

Для полинома второго порядка A₂(s)=a₂s² +a₁s+a₀ приведенное условие устойчивости также является не только необходимым, но и достаточным, так как :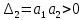



Для полиномов выше второго порядка это необходимое условие уже не является достаточным.

Здесь ограничимся рассмотрением критерия устойчивости Гурвица для полинома 3-го порядка.

Для полинома A₃(s)=a₃s^3+a₂s^2+a₁s+a₀ имеют место следующие соотношения, получаемые из сравнения произведений “средних” коэффициентов a₂a₁ и “крайних” коэффициентов a₃a₀:

• 
  при a₂a₁  a₃a₀ все три корня – левые (система устойчива);
  
• 
  при a₂a₁ a₃a₀ пара комплексно-сопряженных корней – правые (система неустойчива);
  
• 
  при a₂a₁= a₃a₀ пара сопряженных корней – чисто мнимые, то есть корни располагаются на оси мнимых (система находится на колебательной границе устойчивости).
  

Проведем анализ устойчивости СУ, модель которой показана на рис.4.1 (подразд.4.1). В общем виде оператор W_Р(s)записан в выражении (4.1) – см.подразд.4.2. Приведем его к одной дробно-рациональной функции: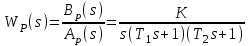

. (7.3)

Запишем теперь в общем виде характеристический полином замкнутой СУ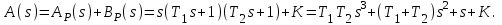

(7.4)

В результате имеем

a_3=T₁T₂, a_2=T₁ +T₂, a_1=1,a_0=K. (7.5)

Определим устойчивость этой СУ при K =10, T₁ =T_2=1с. При таких значениях параметров имеем a₂a₁ a₃a₀ – система неустойчива.

Проанализируем влияние на устойчивость этой СУ усиления в контуре. Зафиксируем значения постоянных времени и будем варьировать параметр K.Из (7.5) видно, что этот параметр входит только в младший коэффициент характеристического полинома (a_0=K). При достаточном уменьшении коэффициента усиления неравенство a₂a₁a₃a₀ поменяет знак: a₂a₁  a₃a₀.

Коэффициент усиления контура обратной связи, при котором система оказывается на границе устойчивости, называется критическим коэффициентом усиления. Для данной СУ, с учетом (7.5), получим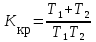

. (7.6)

Для установленных параметров (T₁ =T₂=1 с) получаем K_кр =2.

Для всех K K_кр имеем устойчивую СУ.

Н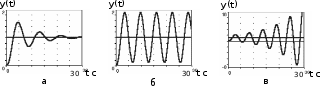
а рис.7.1 изображены переходные процессы в рассматриваемой системе при различных коэффициентах усиления.

Рис.7.1

На рис.7.1,а приведен процесс при K=0.5K_кр=1, на рис.7.1,б  при K=K_кр =2, и на рис.7.1,в  процесс при K=1.5K_кр=3.

Список литературы

1. Техническая кибернетика. Теория автоматического регулирования. Кн.2. Анализ и синтез линейных непрерывных и дискретных систем автоматического регулирования/ Под ред. В.В.Солодовникова. – М.: Машиностроение, 1967.

2. Задачник по теории автоматического регулирования/ Ю.И.Топчеев, А.П.Ципляков. М:. Машиностроение, 1977.

3. Автоматическое регулирование. Теория и элементы систем/ Н.Н.Иващенко – Изд. 4-е, перераб. и доп. - М:. Машиностроение, 1978.

4. Теория систем автоматического управления/ В.А.Бесекерский, Е.П.Попов – Изд. 4-е, перераб. и доп. - СПб.: Изд-во «Профессия», 2003.

5. Анализ и синтез систем управления. Теория, методы, примеры решения типовых задач с использованием персонального компьютера/ Д.Х.Имаев, З.Ковальски, Л.Б.Пошехонов, В.Б.Яковлев идр. СПб, Гданьск, Сургут, Томск, 1998.

6. СПб.: Изд-во СПбГЭТУ. Теория управления/А. А. Алексеев, Д. Х. Имаев, Н. Н. Кузьмин, В. Б. Яковлев “ЛЭТИ”, 1999.

7. Теория автоматического управления: Учеб. для вузов/ С.Е.Душин, Н.С.Зотов, Д.Х.Имаев и др. Под ред. В.Б.Яковлева – М,: Высш. шк., 2003.

8, Основы теории управления. Л.Б. Пошехонов, учебное пособие ,»ЛЭТИ»,2006 г.