Лекция по ОснАУ. лекции ОАУ часть1. Основы автоматического управления
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
|
3.3.Идеальное дифференцирующее звено (дифференциатор) Дифференциальное уравнение звена имеет следующий вид:   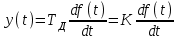 . (3.13) . (3.13)Передаточная функция дифференциатора: 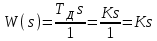 , (3.14) , (3.14)где K=Tд . Параметр Tд называется постоянной дифференцирования, K коэффициентом передачи дифференциатора. Далее будет использоваться запись ПФ дифференциатора в виде W(s)=Ks. Подадим на вход дифференцирующего звена единичное ступенчатое воздействие f(t)=1(t). Изображение такой функции F(s)=1/s. Изображение сигнала на выходе дифференциатора Y(s)=F(s)W(s)=K. Обратное преобразование Лапласа дает реакцию в виде -функции с площадью, равной K, т.е. y(t)=K(t). Запишем частотный оператор дифференцирующего звена: 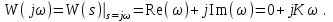 (3.15) (3.15)AЧХ 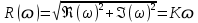 (3.16) Модуль ЛАЧХ (дБ) 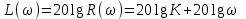 . (3.17) . (3.17)ФЧХ интегрирующего звена 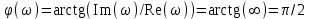 . (3.18) . (3.18)  Рис. 3.6 Рассмотрим АФХ, которая определяется выражением (3.15) – см. рис.3.6. Все точки АФХ располагаются на положительной части оси мнимых. При =0 дифференциатор имеет нулевое усиление, а при увеличении частоты модуль ЧХ R(), как видно из (3.16), монотонно увеличивается. Фазовый сдвиг на всех частотах составляет +/2. ЛЧХ дифференциатора (выражения (3.16), (3.17), (3.18)) приведены на рис.3.7 (построены при K=10). 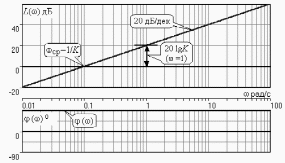 Рис. 3.7 ЛАХ представляет собой прямую, имеющую наклон +20дБ/дек; это означает, что при увеличении частоты в 10 раз модуль ЧХ увеличивается также в 10 раз. Действительно, определим изменение модуля на десятикратном интервале изменения частоты в любом месте диапазона: L=L(10i) L(i) = 20lgR(10i) 20 lgR(i)= = (20 lgK + 20 lg(10) + 20lg(i)) (20 lgK + 20 lg(i))= +20дБ . Для определения местоположения ЛАХ найдем точку L(ср)=0дБ, т.е. место пересечения ЛАХ с осью частот. Из (3.16) видно, что R()=1 при =1/K. Проведенная через эту точку прямая линия с наклоном +20дБ/дек и является ЛАХ дифференциатора с заданным коэффициентом передачи K. Найдем также характерную точку при =1. Из (3.17) следует, что на данной частоте, как и у интегратора 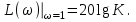 Прямая, проведенная через эту точку и через точку на оси частот =1/K, будет иметь наклон +20дБ/дек. Заметим, что для дифференциатора с K =1 обе характерные точки совпадают (ср=1). ФЧХ дифференцирующего звена, как следует из (3.18), представляет собой прямую линию, параллельную оси частот – см. рис.3.7. При изменении коэффициента передачи (единственного параметра дифференциатора) ЛАХ будет смещаться параллельно самой себе: подниматься при увеличении K или опускаться при уменьшении K. Величина L смещения ЛАХ при изменениии Kв K раз будет составлять L = 20lg(K) дБ. Например, при увеличении K в 20 раз ЛАХ поднимется на 26 дБ, а при уменьшении K в 5 раз опуститься на 14 дБ. 3.4. Апериодическое звено первого порядка Дифференциальное уравнение имеет следующий вид   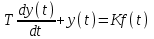 . (3.19) . (3.19)Передаточная функция 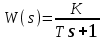 . (3.20) . (3.20)Параметр K называется коэффициентом передачи, T (с) постоянной времени. Изображение сигнала на выходе звена при подаче на вход единичного ступенчатого воздействия 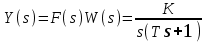 . (3.21) . (3.21)Обратное преобразование Лапласа дает переходный процесс: 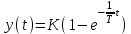 . (3.22) . (3.22)  Рис. 3.8 Таким образом, при реакции на единичное ступенчатое воздействие выходная координата стремится к установившемуся значению K по экспоненциальной зависимости – см.рис.3.8. За t=3T выходной сигнал достигает 95% от своего установившегося значения и переходный процесс принято считать законченным. Частотный оператор апериодического звена: 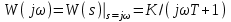 . (3.23) . (3.23)Для получения AФХ выделим вещественную и мнимую части этой комлексной функции, для чего дробь в (3.23) домножим и разделим на комплексно-сопряженное знаменателю выражение. Выполнив соответству-ющие преобразования, получим: 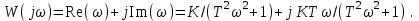 (3.24) (3.24)Можно показать [3], что на комплексной плоскости (3.24) представляет собой уравнение окружности с центром в точке (Re=K/2,Im=0). При изменении частоты от 0 до конец вектора R() описывает полуокружность в первом квадранте комплексной плоскости – см.рис.3.9. Используя (3.24), получим выражение для модуля и фазы ЧХ звена:  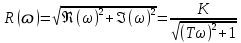   Рис. 3.9 Рис. 3.9(3.25) и 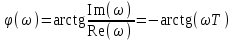 . (3.26) . (3.26)Из этих выражений видно, что на нулевой частоте R(0)=K, (0)=0o, т.е. апериодическое звено ведет себя как пропорциональное звено. При увеличении частоты модуль монотонно убывает и стремится к нулю, а фазовый сдвиг стремится к –/2. Модуль ЛАЧХ (дБ) 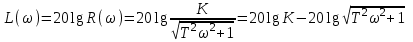 . (3.27) . (3.27)ЛЧХ для апериодического звена с параметрами K=10, T=1c приведены на рис. 3.10. 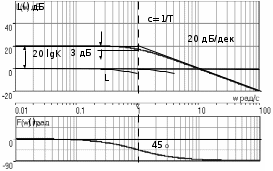 Рис. 3.10 Рассмотрим подробно способ построения ЛАЧХ без вычисления множества точек этой характеристики. Определим так называемую частоту сопряжения с=1/T. На ЛЧХ проведем вертикальную штриховую линию при значении частоты =с (для рассматриваемого примера с=1рад/с – см.рис.3.10). Будем отдельно строить участки ЛАХ для с и с. Рассмотрим диапазон низких частот, который для апериодического звена определим как с. При этом, с учетом (3.25) имеем 2T21 и из (3.27) получаем L() 20lgK – см. рис. 3.10. Проведем прямую линию асимптоту параллельно оси частот на расстоянии 20 lg K от оси частот влево от линии сопряжения с=1/ T. Теперь рассмотрим диапазон высоких частот с. При этом имеем 2T21 и из (3.27) получаем L() 20lg(K/T)=20lg((K/T)/). Последнее выражение соответствует зависимости модуля ЧХ для интегрирующего звена с коэффициентом передачи (K/T) – см. (3.10), (3.11). Его ЛАХ представляет собой прямую линию с наклоном –20дБ/дек; частота среза для такой характеристики ср=(K/T). На частоте сопряжения имеем L(с)=20lgK. В соответствии со сказанным из точки L(с)=20lgK в сторону высоких частот проведем прямую линию с наклоном –20дБ/дек . Полученная ЛАХ, состоящая из двух отрезков прямой линии, которые сопрягаются на частоте с, называется асимтотической ЛАХ – см. рис.3.10. Существенные с позиции расчетов отличия точной ЛАХ от асимтотической ЛАХ будут проявляться в окрестности с, где значения составляющей 2T2 будут соизмеримы с единицей (см. выражение (3.27)). На рис.3.10 изображены асимптотическая ЛАХ (тонкие прямые линии) и точная ЛАХ (жирная кривая). Разница L() между точной и асимптотической ЛАХ называется поправкой, которая также изображена на этом рисунке. Максимальное отличие имеет место на частоте сопряжения и составляет L(с) –3 дБ. На логарифмической ЧХ поправка симметрична относительно линии сопряжения. С достаточной для практических целей точностью можно считать, что L()0 для диапазонов частот (с/3) и 3с. При построении ЛАХ без вычисления точных значений L() в этом диапазоне достаточно наметить две точки на асимптотических ЛАХ при (с/3) и при 3с, а также смещенную на –3 дБ точку сопряжения асимптот, и соединить эти три точки плавной линией – см. рис.3.10. Полученная таким образом уточненная ЛАХ будет иметь достаточную для практических расчетов точность построения. ФЧХ на частоте сопряжения с =1/T , как следует из (3.26), имеет значение (с)=45o. Как видно из рис.3.10, при логарифмическом масштабе оси частот ФЧХ апериодического звена симметрична относительно точки (с)= 45o. При смещении на декаду влево от с=1/T, имеем (0.1с)6o, при смещении на декаду вправо (10с)84o. Таким образом, на частотный диапазон [0.1с,10с] приходится основное изменение фазы ЧХ апериодического звена. В выражение (3.26) не входит параметр K. При построении ЛЧХ в одном и том же масштабе, для любого апериодического звена ЛФЧХ представляет собой одну и ту же кривую, точка (с)=45o которой устанавливается под частотной осью на значении с=1/T. В операторе звена (3.20) зафиксируем постоянную времени T и будем варьировать коэффициент передачи K. В ЛЧХ не изменится местоположение частоты сопряжения; ФЧХ также останется без изменений. ЛАХ будет смещаться параллельно самой себе: подниматься при увеличении K или опускаться при уменьшении K. Смещение ЛАХ L при изменениии Kв K раз будет составлять L = 20lg(K) дБ. Например, при увеличении K в 5 раз ЛАХ поднимется на 14 дБ, а при уменьшении K в 10 раз опуститься на 20 дБ. В операторе звена (3.20) зафиксируем коэффициент передачи K и будем варьировать постоянную времени T, определяющую инерционность апериодического звена. Это вызовет смещение линии сопряжения при с=1/T. Увеличение T приводит к уменьшению частоты сопряжения и, как следствие, полосы пропускания звена. Переходный процесс будет затягиваться – см.(3.22). Уменьшение T вызывает обратную картину. Параллельный оси частот низкочастотный участок асимптотической ЛАХ (слева от частоты сопряжения) остается без изменений при варьировании постоянной времени T. ФЧХ при изменении постоянной времени T будет смещаться влево при увеличении T, или вправо при его уменьшении, следуя точкой (с)=45o за линией сопряжения на с=1/T. Отдельно заметим, что при K=1 низкочастотный участок асимптотической ЛАХ проходит по оси частот, так как 20lg(1) = 0 дБ. Эта особенность будет использована при построении ЛАХ последовательного соединения типовых звеньев СУ. 3.5. Пропорционально-дифференцирующее звено Дифференциальное уравнение имеет следующий вид  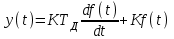 . (3.28) . (3.28)Передаточная функция  . (3.29) . (3.29)Параметр K называется коэффициентом передачи, TД=(с.) постоянная времени. Изображение сигнала на выходе звена при подаче на вход единичного ступенчатого воздействия 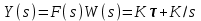 . (3.30) . (3.30)  Рис. 3.11 Обратное преобразование Лапласа дает переходный процесс: 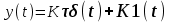 . (3.31) . (3.31)Таким образом, при реакции на единичное ступенчатое воздействие выходная координата содержит две составляющие: -функцию с площадью, равной K, и постоянный сигнал величины K – см.рис.3.11. Частотный оператор пропорционально-дифференцирующего звена: 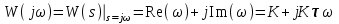 . (3.32) . (3.32)Это выражение позволяет сразу сделать выводы о виде АФХ. Действительно, Re()=Const=K, Im(0)=0, Im()0 при 0 и возрастает пропорционально частоте – см.рис.3.12.   Рис. 3.12 Из (3.32) получим выражение для модуля и фазы ЧХ звена: 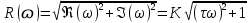 , (3.33) 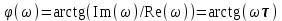 . (3.34) . (3.34)Из этих выражений видно, что на нулевой частоте R(0)=K, (0)=0o, то есть пропорцио-нально-дифференцирующее звено ведет себя как пропорциональное звено. При увеличении частоты модуль монотонно возрастает до , а фазовый сдвиг стремится к /2. Модуль ЛАЧХ (дБ) 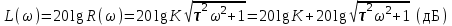 . (3.35) . (3.35)ЛЧХ для пропорционально-дифференцирующего звена с параметрами K=10, =1 c приведены на рис. 3.13. О виде ЛАХ можно судить, сравнив выражения (3.35) и (3.27) и ознакомившись со способом построения ЧХ апериодического звена – см. подразд. 3.4. Частота сопряжения с=1/. Также отдельно строятся участки ЛАХ для с и с. Видно, что ЛАХ пропорционально-дифференцирующего звена является зеркальным отображением (относительно линии 20lgK) ЛАХ звена апериодического с совпадающими параметрами коэффициентами передачи и постоянными времени. 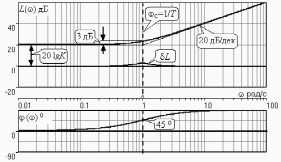 Рис. 3.13 При сопоставлении (3.34) с (3.26) видно, что зависимости фазы от частоты пропорционально-дифференцирующего и апериодического звеньев отличаются только знаком. Поэтому их ФЧХ являются зеркальным отображением друг друга относительно линии ()=0o – см. рис.3.13. Вариации параметров пропорционально-дифференцирующего звена вызывают изменения в ЛЧХ, аналогичные апериодическому звену. Также отдельно заметим, что при K=1 низкочастотный участок асимптотической ЛАХ проходит по оси частот, так как 20lg1=0дБ; это обстоятельство будет использовано при построении ЛАХ последовательного соединения типовых звеньев СУ. 3.6. Колебательное звено 2-го порядка Звено 2-го порядка может описывать колебательные процессы. Дифферециальное уравнение звена   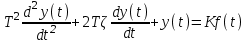 . (3.36) . (3.36)Передаточная функция звена: 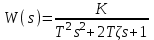 , (3.37) , (3.37)где K коэффициент передачи, T постоянная времени. Параметр ζ коэффициент демпфирования определяет колебательность процесса. Корни квадратного уравнения – знаменателя ПФ – определяют вид переходнеого процесса. При ζ>1 имеем пару разных действительных корней и (3.37) может быть приведено к виду 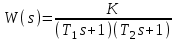 . (3.38) . (3.38)В этом случае звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка; реакция на ступенчатое воздействие будет представлять собой апериодический процесс. При ζ=1 выражение (3.37) приводится к виду 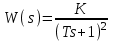 . (3.39) . (3.39)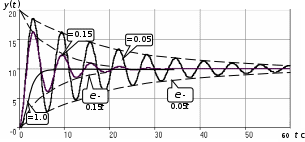 Знаменатель ПФ в (3.39) имеет пару кратных действительных корней s1,2=1/T. Апериодический переходный процесс, соответствующий этому случаю для звена с параметрами K=10, T=1c представлен на рис.3.14 (кривая обозначена соответствующим значением коэффициента демпфирования ζ=1). Рис.3.14 В диапазоне значений коэффициента демпфирования 0<ζ<1 знаменатель ПФ (характеристический полином звена) имеет пару комплексно-сопряженных корней 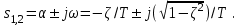 (3.40) (3.40)Реакция на единичное ступенчатое воздействие будет определяться выражением [2], [4] 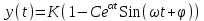 , (3.41) , (3.41)где 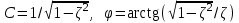 . (3.42) . (3.42)На рис.3.14 представлены два колебательных процесса для звена с параметрами K=10, T=1c. при значениях коэффициента демпфирования ζ=0.15 и ζ=0.05. Видно, что время окончания процессов определяет огибающая et. Количество периодов колебаний за время протекания процесса определяется соотношением мнимой и вещественной частей. На рассматриваемом примере колебательного звена 2-го порядка определим корневые показатели качества процессов в СУ. абсолютное затухание. Определяется как расстояние от мнимой оси до ближайшего корня. Если корень действительный (для рассматриваемого примера это имеет место при ζ1), то =min|si|. Если ближайшей к мнимой оси оказывается пара комплексно-сопряженных корней si,i+1=iji (для данного примера при ζ<1), то =min|i|. Абсолютное затухание определяет время окончания переходного процесса – см.рис.3.14. Значению ζ=0.15 соответствует пара s1,2=0.15j0.989. Ограничивающая экспонента e0.15t “давит” колебания до значения 5% от начального за три своих постоянных времени, что определяет время окончания процесса tp=3(1/0.15)=20c. Для случая ζ=0.05 имеем пару корней s1,2=0.05j0.999 и tp=3(1/0.05)=60c – см.рис.3.14. относительное затухание, или колебательность. Определяется как отношение мнимой части к вещественной части той пары комплексно-сопряженных корней, для которой это отношение максимально, т.е. =max(Imsi/Resi)=max(i/i). Относительное затухание характеризует количество периодов колебаний с частотй , которые “успеют” уложится за время tp. Само значение приблизительно равно числу экстремумов (т.е. числу полупериодов) процесса за время его протекания tp. Для рассматриваемого примера при ζ=0.15 имеем 6.6 и за время tp=20с уложились три полных периода колебаний переходного процесса. При ζ=0.05 имеем 20 и за время tp=60 с. успели уложится десять периодов. 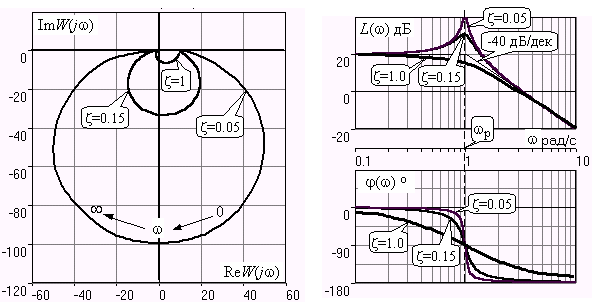 а б Рис. 3.15 На рис.3.15,а представлены АФХ, а на рис.3.15,б ЛЧХ рассматриваемого колебательного звена. В диапазоне низких частот 1/T звено ведет себя как пропорциональное. При >>1/T модуль ЧХ убывает со скоростью –40 дБ/дек, а фаза стремиться к . Комплексно-сопряженные корни порождают на ЧХ резонанс при 1/T, степень проявления которого увеличивается с ростом (т.е. при уменьшении коэффициента ). С уменьшением резонанс на ЛЧХ становится более узким и высоким, а изменение фазы более резким см. рис.3.15.б. ЛЧХ могут быть построены следующим образом. Сначала строится асимптотическая ЛАХ для значения =1 см. рис.3.15,б. Затем в окрестности частоты сопряжения с=1/T вводится поправка, зависящая от величины коэффициента . Эта поправка может быть взята из таблиц, в которых представлено семейство таких поправок при различных значениях при изменении частоты относительно частоты сопряжения с [3], [4]. В этих таблицах также приводится семейство ФЧХ для разных значений см. рис.3.15,б. На примере колебательного звена введем также следующие частотные показатели качества СУ. р – частота резонанса, на которой имеет место резонанс на ЧХ; с этой круговой частотой и проявляется колебательная составляющая переходного процесса. M – показатель колебательности (не путать с корневым показателем колебательность или относительное затухание ); определяется по АЧХ: 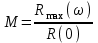 . (3.43) . (3.43)Значение M говорит о числе периодов колебаний за время протекания переходного процесса. Например, для рассматриваемого звена при =0.15 имеем M=3.36; из рис.3.14 видно, что за время процесса имеют место приблизительно три периода колебаний. При =0.05 показатель колебательности M=10 и переходный процесс содержит приблизительно десять периодов колебаний на частоте резонанса. |
