Глава 1_ANSYS. Основы работы в программе ansys 1 Основные элементы управления в ansys
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
|
Выбор типа элемента и задание его опций Для выбора типа элемента используется следующий пункт меню: Main Menu > Preprocessor > Element Type > Add/Edit/Delete В окне Element Typeбудут отображаться все выбранные элементы. Например, нам необходимо выбрать элемент Beam3. Для этого в окне Element Typeнажимаем кнопку Add… В левом поле появившегося окна выбираем Beam,в правом — 2D elastic 3. В строке Element Type reference numberуказывается номер ссылки, ОК(рис.1.48). 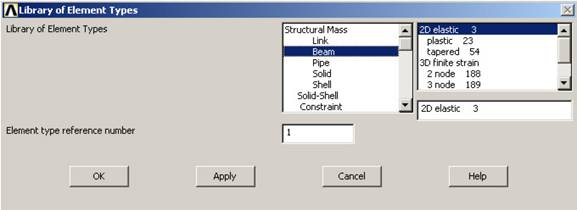 Рис.1.48 Для задания опций элемента нажимаем в окне Element Typeкнопку Options… В появившемся окне в строке Output at extra intermed pts K9выбираем 9 in intermed pts, ОК(рис.1.49). 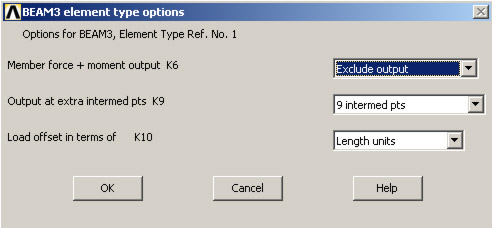 Рис.1.49 Закрываем окно Element Typeнажатием кнопки Close.Опция K9для Beam4позволяет задать расчет искомых величин в промежуточных положениях каждого элемента. Для каждого элемента задаются свои опции, при этом для некоторых элементов (например, для Link 1) задание опций вообще не предусмотрено. Определение вещественных констант элемента Вещественные константы элемента являются свойствами, которые зависят от типа элемента, например свойства сечения элемента в Beam3 (на основании предыдущего примера): Main Menu > Preprocessor > Real Constants > Add/Edit/Delete В окне Real Constants нажимаем кнопку Add...Открывшееся окно ElementTypeforRealConstants после нажатия ОКвыводит на монитор окноRealConstantsforBEAM3, в котором задаются следующие характеристики: AREA — площадь поперечного сечения IZZ — осевой момент инерции сечения HEIGHT — высота сечения SHEARZ — постоянная отклонения сдвига ISTRN — начальная деформация ADDMAS — дополнительная масса на единицу длины (рис.1.50). 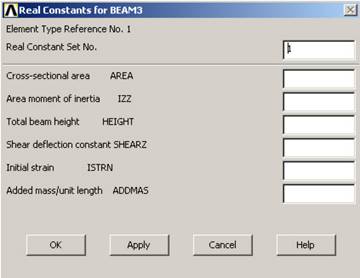 Рис.1.50 Не все типы элементов требуют задания вещественных констант, а разные элементы одного типа могут иметь различные их значения. Так же, как и у типов элементов, каждый набор констант имеет номер ссылки. Определение физических свойств материала При использовании того или иного конечного элемента, как правило, нужно задавать физические свойства материала. Задание физических свойств материала осуществляется с помощью пункта главного меню Main Menu > Preprocessor > Material Props > Material Models… При этом выводится окно Material Model Behavior, в котором выбирают необходимые характеристики и задают их числовые значения (рис.1.51). 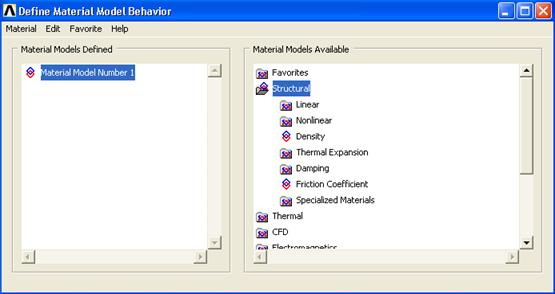 Рис.1.51 Это диалоговое окно разделено на две части. Слева (Material Models Defined) располагается перечень номеров моделей материалов, определенных на момент открытия окна (по умолчанию определено одно имя материала — Material Model Number 1). В правой части (Material Models Available) можно выбрать требуемую для решения задачи модель материала; здесь реализована древовидная структура, двигаясь по которой, переходят от общих пунктов к более детальным. Для решения задач инженерной механики используется пункт Structural, щелчок мышью на котором открывает доступ к подпунктам Linear(линейное деформирование) иNonlinear (нелинейное). При необходимости можно использовать в рамках одной задачи несколько материалов с разными свойствами: Define Material Model Behavior > Material > New Model… В открывшемся окне вводится порядковый номер следующего материала; при этом в окне Material Models Defined появится новая строка —Material Model Number 2и т.д. Линейные свойства материала (Elastic) могут быть постоянными или зависеть от температуры, могут быть изотропными, ортотропными или анизотропными. Можно задавать соответствующую направлению метку того или иного свойства, например, EX, EY, EZ для модуля упругости I рода. Если материал изотропный, то его свойства задаются только в направлении оси Х; свойства по остальным направлениям автоматически принимаются такими же. С целью снижения объема вводимой информации по умолчанию в программе также принимается: 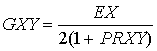 (модуль сдвига). (модуль сдвига).Свойства материала, зависящие от температуры, в ANSYS задаются в виде полинома (от первого порядка до четвертого) или в виде табличных данных. Температуро зависимые свойства материала учитываются программой при составлении матриц элементов. Нелинейные свойства материала (например, данные пластичности) обычно задаются в виде таблиц. Аналогичным образом задаются анизотропные свойства упругости, которые вводятся в виде матрицы (отметим, что эти свойства отличаются от анизотропной пластичности, которая требует задания разных зависимостей растяжения-сжатия в разных направлениях). Анизотропную упругость поддерживают элементы PLANE13, SOLID5, SOLID64, SOLID98. Рассмотрим пример, демонстрирующий задание нелинейной изотропной модели материала, использующей Voce law, в структурном анализе. 1. Выбираем пункт меню Preprocessor >Material Props>Material Models Появляется диалоговое окно Define Material Model Behavior. 2. В окне Material Models Availableдважды щелкаем «мышью» по опциям Structural,Linear,Elastic,Isotropic. 3. Вводим значения свойств материала (модуль упругости EX и коэффициент Пуассона PRXY). OK. В окне Material Models Defined появляетсяметка используемого материала ? Material Model Number 1. 4. В окне Material Models Availableдважды кликните по следующим опциям: Nonlinear, Inelastic, Rate Independent, Isotropic Hardening Plasticity,Mises Plasticity, Nonlinear. Появляется диалоговое окно, включающее таблицу, в которой можно добавить столбцы температуры или ряды данных. Температурное поле завуалировано, так как ANSYS по умолчанию предполагает, что вводятся температуро независимые данные. Вследствие того, что в данном примере используются температуро зависимые свойства материала (включают две температуры), нужно добавить другой температурный столбец. 5. Нажимаем кнопку Add Temperature. Появляется второй столбец. 6. Вводим первую температуру в строке Temperatureи столбце T1. 7. Вводим константы для первой температуры. 8. Вводим вторую температуру в строке Temperatureи столбце T2 и константы для второй температуры. Если есть необходимость ввода констант для третьей температуры, то следует разместить курсор в строке Temperatureстолбца T2, затем нажатьAdd Temperature. После этого появится третий столбец. Рассматриваемая модель материала требует задания четырех констант для каждой из температур. При использовании другой модели, разрешающей большее количество констант, была бы активной кнопка Add Row. 9. Нажимаем OK. Закрывается диалоговое окно. Свойства, заданного материала появляются под Material Model Number 1. Рассмотрим еще один пример, в котором необходимо внести изменения в данные модели материала. Предположим, что предыдущий пример выполнен, и модель материала отображена в окне Material Models Defined. Существуют два метода изменения данных: изменениеданных внутри существующего свойства материала; копирование всего набора свойств материала из другой модели с последующим изменением свойств. Пусть необходимо изменить заданные значения нелинейной изотропной модели. Последовательность действий будет такой: 1. Дважды кликаем Nonlinear_Isotropic'>Nonlinear Isotropic. Появляется диалоговое окно. 2. Изменяем данные в соответствующих полях, OK. Допустим, что одна модель материала построена, а вторая модель должна быть аналогична первой за исключением дополнительной температуры и соответствующих констант. Выполняем следующие действия: 1. В диалоговом окне Define Material Model Behaviorвыбираем пункт меню Edit > Copy, затем выбираем 1 в Material number, и вводим 2 в Material number, OK. Окно Material Models Definedтеперь содержит в своем списке Material Model Number 2. При этом свойства Material Model Number 2Material Model Number 1 будут одинаковыми. 2. Дважды кликаем по Nonlinear Isotropicпод Material Model Number 2. Появляется диалоговое окно. 3. Ставим курсор на крайний правый ряд Temperatureи нажимаем Add Temperature. Появляется столбец T3. 4. В этот новый столбец вводим значение температуры и четыре константы для этой температуры, OK. Диалоговое окно закрывается. Если вы щелкнутьNonlinear Isotropicпод Material Model Number 2, появится диалоговое окно с измененными данными. Рассмотрим задание материала, исходя из комбинации двух моделей материала, и построим модель, моделирующую циклическое смягчение. Используются нелинейная изотропная модель и модель Chaboche. 1. Выбираем пункт меню Preprocessor > Material Props > Material Models Появляется диалоговое окно Define Material Model Behavior. 2. В окне Material Models Availableдважды кликаем Structural, Linear, Elastic, Isotropic. Появляется диалоговое окно. 3. Вводим значения модуля упругости EX и коэффициента Пуассона PRXY). 4. В окне Material Models Available дважды щелкаем Nonlinear, Inelastic, Rate Independent, Combined Kinematic and Isotropic Hardening Plasticity,Mises Plasticity. 5. Дважды кликаем Chaboche and Nonlinear Isotropic. Появляется диалоговое окно для задания констант модели Chaboche. 6. Вводим первые три константы модели Chaboche. 7. Модель Chaboche позволяет задать большее количество констант. При необходимости ввода следующей константы нажимаем Add Row и вводим нужное значение. 8. OK, диалоговое окно закрывается, и появляется другое диалоговое окно для задания констант нелинейной изотропной модели. 9. Вводим константы, связанные с нелинейной изотропной моделью. 10. OK, диалоговое окно закрывается. Под Material Model Number 1приведено следующее: Linear Isotropic,Chaboche, andNonlinear Isotropic. Способы построения конечно-элементной сетки После построения твердотельной модели, создается ее конечно-элементный аналог (т.е. сетка узлов и элементов). В ANSYS предусмотрено четыре способа генерации сетки: использование метода экструзии, создание упорядоченной сетки, создание произвольной сетки (автоматически) и адаптивное построение. Метод экструзии (выдавливания) используется для превращения областей двумерной сетки в трехмерные объекты, состоящие из параллелепипедов, клиновидных элементов или их комбинации. Процесс экструзии осуществляется с помощью процедур смещения из плоскости, буксировки, поступательного и вращательного перемещений. Построение упорядоченной сетки требует предварительного разбиения модели на отдельные составные части с простой геометрией, а затем выбора таких атрибутов элемента и соответствующих команд управления качеством сетки, чтобы можно было построить конечно-элементную модель с упорядоченной сеткой. Создаваемая программой упорядоченная сетка может состоять из шестиугольных, четырехугольных и треугольных элементов. Для получения треугольной сетки программа выделяет области модели, предназначенные для нанесения упорядоченной сетки, создает сначала четырехугольную сетку, а затем превращает ее в сетку из треугольных элементов. Такой способ построения сетки является весьма удобным как при создании сетки из тетраэдров, так и при нанесении сетки на жестких поверхностях при решении контактных задач, где предпочтительно сводить число конечных элементов к минимуму. В качестве дополнительного способа построения упорядоченной сетки на некоторой поверхности используется деление противоположных граничных линий этой поверхности таким образом, чтобы можно было осуществить переход от одного размера сетки к другому. Построение упорядоченной сетки переменного размера возможно только для поверхностей, ограниченных четырьмя линиями (с использованием или без конкатенации, т.е. операции объединения двух последовательностей граничных линий в одну; при этом первая последовательность становится началом результирующей, а вторая — ее хвостом). ANSYS позволяет также строить произвольную сетку, которая может наноситься непосредственно на модель достаточно сложной геометрии — без необходимости строить сетку для отдельных частей и затем собирать их в единую модель. Произвольную сетку можно строить из треугольных, четырехугольных и четырехгранных элементов. Генераторы произвольной сетки обладают широким набором внутренних и внешних опций управления качеством сетки. Например, реализован алгоритм разумного выбора размеров конечного элемента, позволяющий строить сетку элементов с учетом кривизны поверхности модели и наилучшего отображения ее реальной геометрии. Пользователь может выбрать мелкую или крупную сетку элементов, указав в качестве управляющего параметра любое число из диапазона от единицы до десяти. Кроме того, каждый из этих генераторов снабжен алгоритмами сглаживания и рафинирования размеров сетки, что снижает число элементов неудовлетворительной формы и прерываний процедуры построения сетки. Другие доступные средства управления качеством сетки включают указание общего размера элемента, деление граничной линии, размеры в окрестности заданных геометрических точек, коэффициенты растяжения или сжатия вдали от границ, ограничения на кривизну и возможность задания “жестких” точек (т.е. задание точного положения узла вместе с размерами сетки в такой точке). Поскольку тетраэдный генератор работает с учетом размера сетки на соседних частях модели, пользователь имеет возможность указать нужную сетку на границе области до обращения к генератору. Еще один вид контроля качества сетки реализован для двумерных областей, сложных в геометрическом отношении, для которых ручное разбиение на части и последующее построение упорядоченной сетки является обременительным (к ним относятся моделирование некоторых зон потоков жидкости или газа). Для таких случаев программное средство послойного построения сетки дает возможность автоматически генерировать произвольную сетку, профилированную вдоль некоторой преграды и удобную для моделирования явлений, имеющих слоистую структуру. Переход от шестигранной сетки к четырехгранной с использованием пирамидальных элементов весьма удобен для моделирования геометрии на стыке областей с разной сеткой. Имеется возможность автоматически состыковывать такие области без необходимости вводить условия-ограничения или пропускать срединные узлы элементов и избегать математических разрывов в искомых функциях. Некоторые области модели можно достаточно просто разбить на части, для которых строится упорядоченная сетка, тогда как другие ее области могут быть более сложными в геометрическом отношении. Для более простых областей модели можно использовать шестигранные элементы, а для остальных — тетраэдные. Области модели со значительными градиентами искомых величин могут потребовать введения сетки из шестигранных элементов, а для менее критических областей пригодными могут оказаться тетраэдные. Адаптивное построение сетки состоит в том, что после создания твердотельной модели и задания граничных условий программа, по указанию пользователя, генерирует конечно-элементную сетку, выполняет анализ, оценивает ошибку за счет сеточной дискретизации и меняет размер сетки от решения к решению до тех пор, пока расчетная погрешность не станет меньше некоторой наперед заданной величины (или пока не будет достигнуто установленное число итераций). Адаптивное построение модели можно использовать для статического линейного анализа или стационарного теплового расчета. Такая процедура создания сетки может быть выполнена и при наличии нескольких разных условий нагружения. Кроме того, имеется возможность указать те области расчетной модели, для которых уменьшение ошибки дискретизации не столь важно, и исключить их из адаптивной процедуры. Можно настроить процедуру адаптивного построения сетки, исходя из индивидуального подхода к проведению анализа. Возможности программы ANSYS допускают проведение модификации конечно-элементной сетки. Например, могут быть изменены атрибуты узлов и элементов. Если модель состоит из повторяющихся областей, то можно создать сетку только для некоторой области модели, а затем сделать копию этой области. После того как геометрическая модель покрывается сеткой конечных элементов, программа автоматически обеспечивает их взаимо-перекрестный контроль, чтобы гарантировать правильность выполняемых пользователем видоизменений сеточной модели. Такие проверки предотвращают некорректное уничтожение или порчу данных, относящихся к твердотельной и сеточной моделям. Так, например, ключевые точки, линии, поверхности или объемы сеточной модели нельзя уничтожить или переместить до тех пор, пока пользователь явным образом не потребует от программы отменить их автоматический контроль. К другим видам модификации сетки, нанесенной на твердотельную модель, относятся ее измельчение и улучшение формы тетраэдных элементов. Треугольная, четырехугольная и тетраэдная сетки (или произвольное их сочетание) можно локально измельчать, используя интерактивные и “интуитивные” средства. Тетраэдную сетку, независимо от способа ее построения, можно улучшить с помощью процедуры, которая кроме модификации положений узлов, позволяет вводить, удалять и переставлять конечные элементы, обеспечивая тем самым получение сетки высокого качества. |
