Основные понятия математической логики
 Скачать 2.32 Mb.
|
Ещё пример задания:Р-11. На числовой прямой даны два отрезка: P = [10,30] и Q = [25, 55]. Определите наибольшую возможную длину отрезка A, при котором формула ( x A) → ((x P) (x Q) ) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) 10 2) 20 3) 30 4) 45 Решение: для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами A: x А, P: x P, Q: x Q перейдем к более простым обозначениям A → (P + Q) раскроем импликацию через операции НЕ и ИЛИ (  ):  для того, чтобы выражение было истинно при всех x, нужно, чтобы  было истинно там, где ложно  (жёлтая область на рисунке) поэтому максимальный отрезок, где A может быть истинно (и, соответственно, ложно) – это отрезок [10,55], имеющий длину 45Ответ: 4. Ещё пример задания:Р-10. На числовой прямой даны два отрезка: P = [10,20] и Q = [25, 55]. Определите наибольшую возможную длину отрезка A, при котором формула ( x A) → ((x P) (x Q) ) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) 10 2) 20 3) 30 4) 45 Решение: для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами A: x А, P: x P, Q: x Q перейдем к более простым обозначениям A → (P + Q) раскроем импликацию через операции НЕ и ИЛИ ( ): для того, чтобы выражение было истинно при всех x, нужно, чтобы 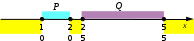было истинно там, где ложно  (жёлтая область на рисунке) поскольку области истинности  и  разделены, максимальный отрезок, где A может быть истинно (и, соответственно, ложно) – это наибольший из отрезков и , то есть отрезок [25,55], имеющий длину 30Ответ: 3. Ещё пример задания:Р-09. На числовой прямой даны два отрезка: P = [14,34] и Q = [24, 44]. Выберите такой отрезок A, что формула ( x A) → ((x P) (x Q) ) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину. 1) [15, 29] 2) [25, 29] 3) [35,39] 4) [49,55] Решение: для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами A: x А, P: x P, Q: x Q перейдем к более простым обозначениям A → (P Q) выражение R = (P Q) истинно для всех значений x, при которых P и Q равны (либо оба ложны, либо оба истинны) нарисуем область истинности выражения R = (P Q) на числовой оси (жёлтые области) 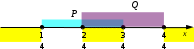 импликация A → R истинна за исключением случая, когда A=1 и R=0, поэтому на полуотрезках [14,24[ и ]34,44], где R=0, выражение A должно быть обязательно ложно; никаких других ограничений не накладывается из предложенных ответов этому условия соответствуют отрезки [25,29] и [49,55]; по условию из них нужно выбрать самый длинный отрезок [25,29] имеет длину 4, а отрезок [49,55] – длину 6, поэтому выбираем отрезок [49, 55] Ответ: 4. |