Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 02.02.2022
• Размер: 2.32 Mb.
• Имя файла: ege15.doc
• Тип: Закон; #349239
• страница: 18 из 50

Ещё пример задания:

Р-08. На числовой прямой даны два отрезка: P = [20, 50] и Q = [10, 60]. Выберите такой отрезок A, что формула

( (x  P) → (x  А) ) /\ ( (x  A) → (x Q) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [5, 40] 2) [15, 54] 3) [30,58] 4) [5, 70]

Решение:

1. 
   в этом выражении две импликации связаны с помощью операции И (конъюнкции), поэтому для истинности всего выражения обе импликации должны быть истинными
   
2. 
   для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами
   

A: x  А, P: x  P, Q: x  Q

3. 
   перейдем к более простым обозначениям в обоих условиях
   

(P → A) /\ (A → Q)

и выразим импликацию через операции ИЛИ и НЕ: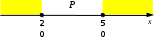

,

4. 
   выражение должно быть истинно на всей числовой оси; обозначим область, которую перекрывает выражение – это две полуоси
   

5. 
   отсюда следует, что отрезок A должен полностью перекрывать отрезок P; этому условию удовлетворяют варианты ответов 2 и 4
   
6. 
   выражение тоже должно быть истинно на всей числовой оси; выражение должно перекрывать все, кроме отрезка, который перекрывает выражение :
   

7. 
   поэтому начало отрезка должно быть внутри отрезка [10,20], а его конец – внутри отрезка [50,60]
   
8. 
   этим условиям удовлетворяет только вариант 2.
   
9. 
   Ответ: 2.
   

Ещё пример задания:

Р-07. На числовой прямой даны два отрезка: Р = [35, 55] и Q = [45, 65]. Выберите такой отрезок А, что обе приведённые ниже формулы истинны при любом значении переменной х:

(x  P) → (x  A)

( (x  А)) → ((x Q))

Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [40,50] 2) [30,60] 3) [30,70] 4) [40, 100]

Решение:

1. 
   для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами
   

A: x  А, P: x  P, Q: x  Q

2. 
   перейдем к более простым обозначениям в первом условии P → A и выразим импликацию через операции ИЛИ и НЕ: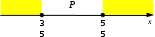
   
3. 
   выражение должно быть истинно на всей числовой оси; обозначим область, которую перекрывает выражение - это две полуоси
   
4. 
   
   
5. 
   отсюда следует, что отрезок A должен полностью перекрывать отрезок P; этому условию удовлетворяют варианты ответов 2 и 3
   
6. 
   аналогично разбираем и преобразуем второе выражение
   

7. 
   и находим, что для того, чтобы обеспечить истинность второго выражения на всей оси отрезок A должен полностью перекрыть отрезок Q; этому условию удовлетворяют варианты ответов 3 и 4
   
8. 
   объединяя результаты п. 5 и 7, получаем, что условию задачи соответствует только отрезок 3.
   
9. 
   Ответ: 3.