Основные понятия математической логики
 Скачать 2.32 Mb.
|
Ещё пример задания:Р-02. На числовой прямой даны три интервала: P = (10, 15), Q = [5, 20] и R = [15,25]. Выберите такой отрезок A, что выражения (x A) → (x P) и (x Q) → (x R) принимают различные значения при любых x. 1) [7, 20] 2) [2, 15] 3) [5,12] 4)[20, 25] Решение (способ 1, отрезки на числовой прямой): обратите внимание, что интервал P – это открытый интервал; это необходимо для того, чтобы можно было выполнить заданное условие в точках стыковки отрезков для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами A: x А, P: x P, Q: x Q, R: x R перейдём к более простым обозначениям:  ,  выразим импликации через операции «ИЛИ» и «НЕ»:  ,  заметим, что неизвестная величина A входит только в выражение  общая идея состоит в том, чтобы построить на числовой оси область истинности для полностью известного выражения  , а затем дополнить отрезок P до «обратной» области, в которой выражение  ложно; это «дополнение» будет соответствовать области  построим область 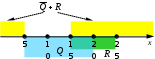 – объединение отрезка R и области вне отрезка Q: теперь рассмотрим область 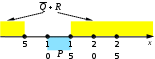 (выделена голубым цветом) чтобы выполнить заданное условие (противоположность значений 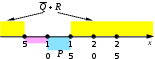 и  при любых x), область истинности выражения должна совпадать с областью, где выражение ложно; для этого выражение должно «перекрыть» всю фиолетовую область (возможно, заходя в область ), но не должно заходить в «жёлтую» область: из предложенных вариантов ответов этим требованиям удовлетворяет только отрезок [5,12] (ответ 3) Ответ: 3. Решение (способ 2, таблицы истинности, Е.А. Смирнов): пп. 1-6 такие же, как и в первом способе решения если рассматривать все значения x на числовой прямой, то логические значения формул могут измениться только при переходе через граничные точки заданных промежутков эти точки (5, 10, 15, 20 и 25) разбивают числовую прямую на несколько интервалов, для каждого из которых можно определить логическое значение выражения 
для упрощения записи не будем рассматривать значения формул на концах отрезков, так как это не влияет на решение по условию выражение  должно быть НЕ равно выражению  при любых значениях x, отсюда можно найти, каким должно быть значение для каждого интервала:
таким образом, среди ответов нужно найти отрезок, который перекрывает отрезок [5,10] и, возможно, заходит внутрь отрезка [10,15] из предложенных вариантов ответов этим требованиям удовлетворяет только отрезок [5,12] (ответ 3) Ответ: 3. |
