Задачи по теории надежности. Практическое 3анятие 1 Определение количественных характеристик надежности по статистическим данным об отказах изделия. Теоретические сведения
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
Задачи для самостоятельного решения Задача 9.9. Радиорелейная станция содержит два приемопередатчика, один из которых используется по назначению, а второй находится в ненагруженном резерве. Определить среднее время безотказной работы станции mt при условии, что для каждого приемопередатчика Задача 9.10. Регистрирующее устройство содержит рабочий блок и блок в нагруженном резерве. Вероятность отказа блока в течение 25 часов q(ti) = 0,1 . Ремонт производится одной бригадой с интенсивностью Задача 9.11. Система связи содержит одно устройство, предназначенное для выполнения задачи и одно устройство в нагруженном резерве. Интенсивность отказов каждого устройства равна Задача9.12. Система сопровождения состоит из рабочего блока и блока в нагруженном резерве. Для каждого блока заданы: λ= 2∙10-3 1/час , μ= 0,2 1/час . Определить время безотказной работы системы. Задача 9.13. Преобразователь “параметр-код” состоит из рабочего блока и блока в нагруженном резерве. Распределения времен между отказами и восстановления показательные с параметрами λ= 8∙10-3 1/час , μ= 0,8 1/час. Требуется определить значения коэффициентов простоя и во сколько раз уменьшается величина коэффициента простоя преобразователя при применении неограниченного восстановления по сравнению с ограниченным. Задача 9.14. Устройство состоит из двух одинаковых блоков, один из которых использутся по прямому назначению, а второй находится в нагруженном резерве. Интенсивность отказов каждого блока λ= 6∙10-3 1/час , интенсивность восстановления μ= 2 1/ час. Ремонт производится одной ремонтной бригадой. Требуется определить коэффициент простоя устройства. Задача 9.15. Усилитель состоит из двух равнонадежных блоков, для каждого из которых λ= 3∙10-3 1/час . Имеется усилитель в ненагруженном резерве. Ремонт производит одна бригада, среднее время ремонта m = 0,5 час . Определить коэффициент простоя усилителя с резервом. Задача 9.16. Усилитель состоит из двух равнонадежных блоков, для каждого из которыхλ= 3∙10-3 1/час . Применено поблочное резервирование усилителя в ненагруженном режиме. Ремонт производит одна бригада, среднее время ремонта m = 0,5 час . Определить коэффициент простоя усилителя с поблочным резервированием. Задача 9.17. Вычислитель состоит из двух одинаково рабочих блоков и одного блока в нагруженном скользящем резерве. Для каждого блока λ= 8∙10-3 1/час ; μ= 1 1/час , ремонтных бригад две. Определить коэффициент простоя вычислителя. Задача 9.18. Вычислитель состоит из двух одинаковых рабочих блоков и одного резервного блока в ненагруженном резерве. Для каждого блока λ= 8∙10-3 1/час ; μ= 1 1/час , ремонтных бригад две. Определить коэффициент простоя вычислителя. Задача 9.19. Генератор импульсов содержит один рабочий блок, один блок в нагруженном резерве и один блок в ненагруженном резерве. При неработоспособности рабочего блока или блока в нагруженном резерве блок из ненагруженного резерва переводится в нагруженный. Задано для каждого блока λ= 10-2 1/час, μ= 0,5 1/час , ремонтная бригада одна . Определить коэффициент простоя генератора. Задача 9.20. Передатчик содержит рабочий блок ( Задача 9.21.Преобразователь частоты содержит один рабочий блок и один блок в нагруженном резерве. Ремонт производится одной бригадой, обеспечивающей среднее время восстановления 0,5 час. Определить предельно допустимую интенсивность отказов преобразователя, чтобы удовлетворялось условие KГ =2∙104 . Задача 9.23. Для нерезервированного изделия, имеющего интенсивность отказов ПРАКТИЧЕСКОЕ 3АНЯТИЕ № 10 Расчет надежности резервированных восстанавливаемых устройств по графику состояний. Теоретические сведения Основным недостатком известных методов оценки надежности резервированных систем является их сложность даже при небольшом числе возможных состояний резервированной системы. Эти методы требуют составления и решения дифференциальных уравнений, описывающих функционирование системы. Большое число состояний системы, например, вычислительной системы (ВС), приводит к большому числу дифференциальных уравнений, которое не дает возможности вычислить количественные характеристики надежности даже с помощью ЦВМ. Этих трудностей в ряде случаев удается избежать, записывая решения в преобразованиях Лапласа непосредственно из графа состояний анализируемого устройства. Рассмотрим методику на простом примере. Пусть граф состояний восстанавливаемого устройства имеет вид, представленный на рис. 10.1. Узлам графа приписаны состояния устройства, а ветвям - возможные переходы из одного состояния в другое с интенсивностями ai и bi. Система отказывает, если она переходит из в состояние k-1. Тогда вероятность застать резервированную восстанавливаемую систему в момент времени t в состоянии отказа КП(t) и вероятность ее отказа Q(t) в течение времени t в преобразованиях Лапласа могут быть записаны в следующем виде: 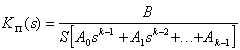 , (10.1) , (10.1) 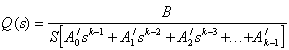 , (10.2) , (10.2)Где k - число состояний системы, равное числу узлов графа состояний; Ai, A/i, B - коэффициенты, зависящие от интенсивностей переходов аi, bi (i=1,2,..., k-1). Коэффициенты Ai, A/i, B можно определить из графа состояний по следующему правилу. Коэффициент при старшем члене sk-1 полинома равен единице, т.е. A0=1. Коэффициент А1 равен сумме всех интенсивностей переходов аi и bi. Коэффициент А2 равен сумме всех попарных произведений интенсивностей переходов, за исключением членов вида aibi, ai+1bi. Из графа (см. рис. 10.1) видно, что члены вида aibi образованы интенсивностями переходов, находящимися в одном кольце графа, а члены ai+1bi - интенсивностями переходов из одного и того же состояния в разные (стрелки,. обозначающие интенсивности переходов, выходят из узлов). Коэффициент А3 равен сумме произведений интенсивностей переходов, взятых по три, за исключением тех членов суммы, в которых встречаются произведения aibi,..., ai+1bi,... Коэффициент Аi при члене Aisk-1-i равен сумме произведений интенсивностей переходов, взятых i (i=1,2,...,k-1), за исключением тех членов суммы, в которых встречаются произведения aibi,..., ai+1bi,... Коэффициент В равен произведению всех интенсивностей отказов и не содержит интенсивностей восстановления, т.е. Коэффициенты Аi/ в выражении (10.2) находятся при известных коэффициентах Аi следующим образом. Если в выражении для коэффициента Аi исключить все члены, содержащие в качестве сомножителя интенсивность перехода bk-1, то полученное выражение будет равно коэффициенту Ai/. Эта закономерность очевидна, так как выражение (10.2) характеризует поведение системы до ее отказа и получено в предположении, что обратного перехода из отказового состояния (состояния k-1) в исправное (состояние k-2) нет. При анализе надежности резервированных восстанавливаемых устройств обычно за критерии надежности принимают функцию готовности КГ(t), коэффициент готовности Функция готовности KГ(t) есть вероятность того, что в любой момент времени t система готова к действию. Наиболее просто из графа состояний находятся коэффициенты простоя и готовности. Очевидно, что Коэффициент готовности KГ является финальной вероятностью пребывания системы в исправном состоянии. Граф состояний резервированной восстанавливаемой системы может иметь более сложный вид, чем изображенный на рис. 10.1. Сложные ветвящиеся графы получаются в случае раздельного резервирования, учета двух характеров отказов, отсутствия контроля моментов отказов отдельных устройств резервированной системы, резервирования неравнонадежных устройств и т.п. В этом случае может быть несколько отказовых состояний. Тогда вероятность того, что резервированная система неисправна в любой момент времени t, вычисляется из соотношения где Pi(t) – вероятность того, что система в момент времени t находится в i-м (отказовом) состоянии, N – число отказовых состояний. Очевидно, что преобразование Лапласа для Pi(t) находится из выражения где Здесь (s) - главный определитель системы; i(s) - частный определитель; k - число состояний системы; ni - число, зависящее от номера отказового состояния. Установлено, что при принятых выше допущениях независимо от вида графа резервированной восстанавливаемой системы коэффициенты Аi определителя (s) находятся по изложенному выше правилу. Оказывается, что число ni и коэффициенты Bi определителя i(s) легко находятся непосредственно из графа состояний и выражений для коэффициентов Ai при соответствующих степенях s определителя (s). Степень полинома числителя i(s) находится из выражения ni=k-1-li , (10.10) где k - число узлов графа состояний; li - число переходов из начального состояния системы, определенного начальными условиями ее функционирования, в состояние i по кратчайшему пути. Если начальным состоянием системы является состояние, когда все устройства системы исправны, то li - номер уровня состояния i, т.е. li равно минимальному числу отказавших устройств системы в состоянии i. Таким образом, степень полинома числителя вероятности Pi(s) пребывания системы в i-м состоянии зависит от номера состояния i и от начальных условий. Так как число переходов li может быть 0,1,2,...,k-1, то степень полинома i(s) на основании (10.10) также может принимать значения ni=0,1,2,...,k-1. Коэффициент при sk-1-j ( j[0;k-1] ) полинома i(s) равен сумме только тех членов коэффициента при sk-j полинома (s), в которых имеются произведения всех интенсивностей переходов из состояния 0 (все элементы исправны) в состояние i по кратчайшему пути, т.е. без восстановления. Получим формулу для определения наработки на отказ tср (tср - математическое ожидание времени между соседними отказами восстанавливаемой системы), воспользовавшись общей формулой для коэффициента готовности вида где tB - среднее время восстановления системы. Из формулы (10.11) получим Пользоваться этой формулой на практике целесообразно в следующих случаях: 1) среднее время восстановления системы tB известно из опыта; 2) система имеет лишь одно отказовое состояниие k-1 (см. рис. 10.1), причем из этого состояния в соседнее состояние (или в соседние состояния) возможен переход с одноой и той же интенсивностью bR-1. Тогда 3) система имеет несколько отказовых состояний (см. рис. 10.2), но интенсивности переходов из этих состояний в соседние одинаковы, т.е. b3=b4 для рис. 10.2. Тогда среднее время восстановления системы для рис. 10.2 равно Случаи 2 и 3 легко распознаются по графу состояний. Тогда для определения наработки на отказ достаточно найти KГ описанным выше способом. На практике наиболее часто встречаются случаи, когда число отказовых состояний системы велико, а значения интенсивностей восстановления зависят от отказового состояния. Тогда tB неизвестно, а наработку на отказ невозможно определить непосредственно по формуле (10.12). Среднее время восстановления и наработку на отказ можно определить, если известны финальные вероятности пребывания системы во всех возможных состояниях и интенсивности переходов из отказовых в предотказовые состояния. Интенсивность восстановления системы с равна сумме произведений интенсивностей переходов из отказовых состояний в исправные на соответствующие вероятности отказовых состояний, т.е. где Ri - вероятность того, что если система откажет, то она попадет в i-е отказовое состояние; i - сумма интенсивностей переходов из i-го отказового состояния во все исправные состояния, граничащие с i-м отказовым состоянием (например, для рис. 10.2 3=b3, 4=b4); е_ - подмножество отказовых состояний, граничащих с исправными. Вероятность Ri вычисляется по формуле 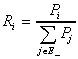 , (10.15) , (10.15)где Pi - финальная вероятность пребывания системы в i-м отказовом состоянии, граничащем с исправным состоянием; Pj - финальная вероятность пребывания системы в j-м отказовом состоянии, граничащем или не граничащем с исправным состоянием; Е_ - подмножество всех отказовых состояний. Интенсивности i легко определить по графу состояний, воспользовавшись соотношением где ij - интенсивность перехода из i-го отказового состояния в j-е граничащее исправное состояние (например, для рис. 10.2 3=32=b3, 4=41=b4); е+ - подмножество исправных состояний, граничащих с отказовыми состояниями. Подставляя значения Ri и i из (10.15) и (10.16) в (10.14), получим 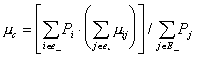 . (10.17) . (10.17)Так как среднее время восстановления и интенсивность восстановления системы связаны соотношением tB=1/c , то  . (10.18) . (10.18)Так как где Е+ - подмножество всех исправных состояний, то  . (10.20) . (10.20)Финальные вероятности пребывания системы в i-м состоянии можно вычислить, воспользовавшись соотношением Соотношение (10.21) с учетом (10.7) - (10.9) примет вид Таким образом, для вычисления финальных вероятностей достаточно определить свободные коэффициенты полиномов si и s по приведенным выше правилам. Заметим, что для определения коэффициента вынужденного простоя или коэффициента готовности можно не искать Kn(s), а находить Kг и KП по формуле (10.5) непосредственно из графа состояний. Из выражения (10.5) следует, что коэффициенты Kг и KП есть отношения вида  , КГ=1-КП , (10.23) , КГ=1-КП , (10.23)где m - число узлов графа, соответствующих отказовым состояниям системы; r=k - m - число узлов графа, соответствующих исправному состоянию системы; Тi - произведение интенсивностей переходов из всех крайних состояний графа в i-е отказовое состояние при движении в i-е состояние по кратчайшему пути в направлении стрелок; Тj - произведение интенсивностей переходов из всех крайних состояний графа в j-е исправное состояние при движении в j-е состояние по кратчайшему пути в направлении стрелок. Руководствуясь установленным правилом, легко найти финальную вероятность пребывания резервированной восстанавливаемой системы в любом i-м состоянии по формуле  , (10.24) , (10.24)где Тi, Tj - произведение интенсивностей переходов из всех крайних состояний соответственно в i-e и j-e состояния при движении по кратчайшему пути в направлении стрелок; k - число узлов графа. |
