практические задания по теории надежности. Практикум по основам надежности технических систем. Методические указания к выполнению практических работ и самостоятельной работы для студентов факультета инженерной механики М. Ргу нефти и газа имени И. М. Губкина, 2018 г. 65 с

• Название: Практикум по основам надежности технических систем. Методические указания к выполнению практических работ и самостоятельной работы для студентов факультета инженерной механики М. Ргу нефти и газа имени И. М. Губкина, 2018 г. 65 с
• Анкор: практические задания по теории надежности
• Дата: 16.12.2021
• Размер: 448.54 Kb.
• Имя файла: mu_teor_aas (1).docx
• Тип: Практикум; #306343
• страница: 3 из 10

МЕТОДИКА РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ПО СТАТИСТИЧЕСКИМ ДАННЫМ

Методика расчета показателей безотказности рассматривается на практическом занятии № 1.

Средний ресурс определяется по формуле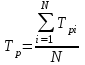

, (3.1)

где Т_pi–ресурс i-го изделия, N – количество объектов, поставленных на испытания или эксплуатацию.

Для нахождения гамма-процентного ресурса необходимо найти такое значение суммарной наработки, вероятность которой равна γ, выраженной в процентах, исходя из условия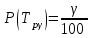

, (3.2)

Значения среднего срока службы и гамма-процентного срока службы определяются аналогично.

Статистическая оценка среднего времени восстановления вычисляется по формуле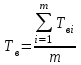

, (3.3)

где Т_вi – время восстановления i-го изделия, m– количество восстановлений рассматриваемых объектов.

Коэффициент готовности К_г определяется по формуле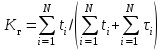

, (3.4)

где t_i – наработка на отказ i-го объекта, τ_i – время восстановления i-го объекта, N– количество рассматриваемых объектов.

Коэффициент технического использования определяется по формуле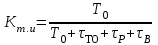

, (3.5)

где T₀ – суммарная наработка объекта, τ_ТО – время планового технического обслуживания, τ_р – время, затрачиваемое на плановый ремонт, τ_в – время, затраченное на внеплановые восстановления.

3. 
   ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
   

1. 
   Изучить методику расчета единичных и комплексных показателей
   
2. 
   Дать определение рассматриваемого показателя
   
3. 
   Определить исходные данные для расчета показателя
   
4. 
   Рассчитать требуемый показатель по формулам (3.1) - (3.5).
   
5. 
   Дать характеристику определяемому показателю по четырем признакам классификации
   
6. 
   Ответить на контрольные вопросы.
   

4. 
   ОФОРМЛЕНИЕ РЕЗУЛЬТАТОВ РАБОТЫ
   

Пример 3.1. На промысловые испытания поставлено 3 буровых насоса. В ходе испытаний у первого насоса было зафиксировано 144 отказа, у второго – 160 отказов, у третьего – 157 отказов. Суммарная наработка на отказ для первого насоса составила 3250 часов, для второго – 3600 часов, для третьего – 2800 часов. Определить среднюю наработку до отказа и средний ресурс бурового насоса.

Решение. Средняя наработка до отказа определяется по формуле (1.5)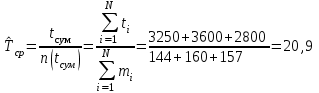

час.

Средний ресурс определяем по формуле (3.1)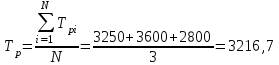

час.

Ответ. Средняя наработка до отказа равна 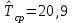час, данный показатель является:

- показателем безотказности;

- единичным, так как характеризует только одно свойств – безотказность.

Средний ресурс равен 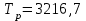час, данный показатель является:

- показателем долговечности;

- единичным, так как характеризует только одно свойств – долговечность.

Пример 3.2. На испытания поставлено 500 изделий. Результаты определения ресурса представлены в таблице 1.4. По данным испытаний определить гамма-процентный ресурс для γ = 95 %, 90 % и 80 %.

Таблица 3.1 – Результаты испытаний изделий

№№	Интервал времени, час	Количество отказавших изделий n(t)
1	0 – 100	24
2	100 – 200	29
3	200 – 300	35
4	300 – 400	15
5	400 – 500	16
6	500 – 600	20
7	600 – 700	35
8	700 – 800	57
9	800 – 900	133
10	900 – 1000	136

Решение. Для определения гамма-процентного ресурса необходимо найти значение наработки, вероятность которой равна 0,95; 0,90; 0,80, согласно формуле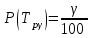

.

Определим количество работоспособных изделий и вероятность безотказной работы на конец каждого временного интервала, результаты расчета сведены в таблицу 3.2.

Таблица 3.2 – Результаты расчета

№№	Интервал времени, час	Количество отказавших изделий n(t)	Количество работоспособных изделий N(t) к концу периода	Вероятность безотказной работы P(t)
1	0 – 100	24	476	0,952
2	100 – 200	29	447	0,894
3	200 – 300	35	412	0,824
4	300 – 400	15	397	0,794
5	400 – 500	16	381	0,762
6	500 – 600	20	361	0,722
7	600 – 700	35	326	0,652
8	700 – 800	57	269	0,538
9	800 – 900	133	136	0,272
10	900 – 1000	136	0	0

По представленному расчету вероятностям 0,95; 0,90 и 0,80 соответствуют значения наработки равные 100, 200 и 400 часов соответственно (выделены в таблице 3.2).

Ответ: гамма-процентные ресурсы равны Т_р95 = 100 часов; Т_р90 = 200 часов; Т_р80 = 400 часов, показатели являются:

- показателем долговечности;

- единичным, так как характеризует только одно свойств – долговечность.

Пример 3.3. В результате наблюдений за работой буровой лебедки получены следующие данные о времени, затраченном на смену тормозных лент, в часах: 2,5; 1,8; 1,8; 2,6; 0,8; 1,2; 0,6; 2,0; 1,6; 3.2. Всего 10 наблюдений. Определить среднее время восстановления буровой лебедки.

Решение: Статистическая оценка среднего времени восстановления вычисляется по формуле (3.3)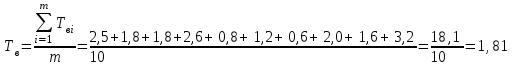

часа,

Ответ: среднее время восстановления равно 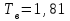часа, показатель является:

- показателем ремонтопригодности;

- единичным, так как характеризует только одно свойств – ремонтопригодность.

Пример 3.4. Определить коэффициент готовности системы при среднем времени восстановления равном 2 часа и средней наработке на отказ равной 100 часов.

Решение: Среднее значение коэффициента готовности К_г вычисляют по формуле (3.4)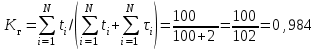

.

Ответ: Коэффициент готовности равен .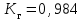

- показателем готовности;

- комплексным, так как характеризует безотказность, ремонтопригодность и готовность.

Пример 3.5. Определить коэффициент технического использования, если известно, что система эксплуатируется в течение 1 года, годовой фонд времени системы составляет 8760 часов. Время проведения ежегодного техосмотра составляет 20 суток, суммарное время, затраченное на ремонтные работы, составляет 20 часов.

Решение: Коэффициент технического использования определяетсяпо формуле (3.5)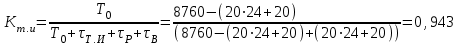

.

Ответ: Коэффициент технического использования равен 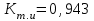, показатель является:

- показателем готовности;

- комплексным, так как характеризует безотказность, ремонтопригодность и готовность.

5. 
   Задания для самостоятельной работы
   

Задача 3.1. На промысловые испытания поставлено 3 насоса. В ходе испытаний у первого насоса было зафиксировано 37 отказа, у второго – 29 отказов, у третьего – 48 отказов. Суммарная наработка на отказ для первого насоса составила 3100 часов, для второго – 2200 часов, для третьего – 2700 часов. Определить среднюю наработку на отказ.

Задача 3.2. На эксплуатацию поставлено 250 изделий. На моменты времени t₁ – t₇ зафиксировано определенное количество отказов (таблица 3.3). Остальные изделия не отказали. Определить средний ресурс.

Таблица 3.3

ti, час	50	100	150	200	250	300	350
n(ti)	5	8	11	15	21	31	9

Задача 3.3. На промысловые испытания поставлено 3 насоса. В ходе испытаний у первого насоса было зафиксировано 37 отказа, у второго – 29 отказов, у третьего – 48 отказов. Суммарная наработка до отказа для первого насоса составила 3100 часов, для второго – 2200 часов, для третьего – 2700 часов. Определить средний ресурс насоса.

Задача 3.4. Длительность проведения технического обслуживания для бурового насоса составляет 45 часов. Межремонтный цикл составляет 2335 часов. Определить коэффициент готовности бурового насоса.

Задача 3.5. Какую длительность восстановления работоспособности должен иметь объект с межремонтным циклом 2000 часов, чтобы коэффициент готовности объекта составлял 0,95.

Задача 3.6. Определить среднее время восстановления компрессора, если на проведение 5 мелких ремонтов было затрачено 30,5 часа.

Задача 3.7. Годовое время работы одной буровой лебедки составляет 3500 часов. За год проводится 4 технических обслуживания продолжительностью 65 часов каждое и 1 средний ремонт продолжительностью 360 часов. Определить коэффициент технического использования буровой лебедки.

Задача 3.8. По данным задачи 3.7 определить коэффициент готовности буровой лебедки.

Задача 3.9. В ходе наблюдений за работой турбобура были зафиксированы отказы в следующие моменты времени: 110, 167, 284, 365, 512, 650 часов работы. Определить среднюю наработку между отказами турбобура.

Задача 3.10. По данным задачи 3.9 определить вероятность безотказной работы и вероятность отказа за 300 и 600 часов работы.

5. Контрольные вопросы:

1. 
   дайте определение средней наработки до отказа и средней наработки на отказ;
   
2. 
   какие показатели используются при определении долговечности;
   
3. 
   как определяются средний и гамма-процентный ресурс;
   
4. 
   как определяются средний и гамма-процентный срок службы,
   
5. 
   дайте характеристику показателям ремонтопригодности: вероятности восстановления, интенсивности восстановления, среднему сроку восстановления;
   
6. 
   дайте характеристику показателям сохраняемости: среднему сроку сохраняемости, гамма-процентному сроку сохраняемости;
   
7. 
   приведите определение и дайте характеристику коэффициенту готовности;
   
8. 
   приведите определение и дайте характеристику коэффициенту оперативной готовности;
   
9. 
   приведите определение и дайте характеристику коэффициенту технического использования;
   
10. 
    приведите определение и дайте характеристику коэффициенту сохранения эффективности.
    

6. 
   Литература:
   

1. 
   Острейковский В.А. Теория надежности: учебник для вузов. – 2-е изд., испр. – М.: Высшая школа, 2008. – 464 с.
   

<sub>Практическая работа № 4

«Определение показателей надежности объектов при различных законах распределения»</sub>

Цель работы:

1. 
   Закрепить теоретические знания, полученные в разделе «Математический аппарат теории надежности».
   
2. 
   Освоить методику нахождения показателей надежности, подчиняющихся различным законам распределения.
   
3. 
   Получить практические навыки расчета показателей надежности, которые подчиняются различным законам распределения, на конкретных примерах.
   

1. 
   ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
   

При решении задач надежности могут использоваться следующие законы распределения: нормальный закон распределения, логарифмически нормальный закон, экспоненциальный закон распределения, распределение Вейбулла и другие.

Нормальный закон распределения является наиболее универсальным, так как он является предельным законом, к которому приближаются другие законы распределения при часто встречающихся типичных условиях.

Нормальному закону распределения подчиняется ряд показателей надежности – суммарная наработка восстанавливаемых изделий до капитального ремонта, время восстановления ремонтируемых изделий и т.п. Для многих восстанавливаемых и невосстанавливаемых изделий наработка на отказ подчиняется нормальному закону.

Закон нормального распределения используется для описания постепенных отказов, когда распределение времени безотказной работы в начале имеет низкую плотность, затем максимальную и далее плотность снижается, т.е. нормальным распределением описывают наработки на отказ элементов и систем вследствие их износа и старения.

Закон экспоненциального распределения случайных величин широко применяется при расчетах надежности элементов электроники. Этот закон описывает надежность работы изделия в период его нормальной эксплуатации, для случая, когда интенсивность отказа величина постоянная, постепенные отказы еще не проявляются и надежность характеризуется внезапными отказами. Отказы вследствие законов старения (коррозии, усталости, изнашивания) не являются внезапными, поэтому данный закон распределения в этом случае применять не рекомендуется.

Экспоненциальным распределением можно описывать время безотказной работы различных изделий: сложных технических систем, эксплуатируемых в период приработки и до появления постепенных отказов; с большим числом последовательно соединенных элементов, если каждый из элементов в отдельности не оказывает влияния на отказы других элементов системы.

В теории надежности используется для описания наработки до отказа и наработки на отказ деталей и узлов в период наступления усталости материала, отказов вследствие изнашивания, отказов подшипников качения и наработки между отказами сложных технических систем, а также процессов восстановления.

В большинстве случаев данное распределение описывает наработку системы с резервированием, время восстановления, а также распределение отказов вследствие износа.

Распределение Вейбулла наиболее широко используется при определении надежности механических систем по результатам эксплуатации или испытаний. Используется при описании усталостной прочности стали, а значит, может быть использовано и для описания изнашивания вследствие многоцикловой фрикционной усталости поверхностных слоев деталей машин. Данное распределение является двухпараметрическим универсальным т. к. при изменении параметров оно в пределе может описывать процессы нормального, логарифмически нормального, экспоненциального и др. распределений.