МУ для лаб.работ СИСТЕМЫ СЧИСЛЕНИЯ. Практикум по теме Системы счисления предназначен для проведения практических занятий с целью получения основных понятий о том, как происходят вычислительные операции в эвм

• Название: Практикум по теме Системы счисления предназначен для проведения практических занятий с целью получения основных понятий о том, как происходят вычислительные операции в эвм
• Дата: 01.03.2023
• Размер: 346.5 Kb.
• Имя файла: МУ для лаб.работ СИСТЕМЫ СЧИСЛЕНИЯ.doc
• Тип: Практикум; #962080
• страница: 7 из 7

6.3Прямой, обратный и дополнительный двоичные коды

В компьютерной арифметике, которая базируется на двоичной системе счисления, операция «вычитания» заменяется операцией «сложения».

Рассмотрим, как это происходит.

Для хранения целых чисел в памяти ЭВМ выделяется фиксированное число двоичных разрядов – бит. Рассмотрим 8–и битовое представление числа. Каждый бит нумеруется «слева – направо» от 0 до 7.


вес разряда
нумерация бит в байте

26

25

24

23

22

21

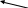2 0

7 6 5 4 3 2 1 0
Старший бит – седьмой – используется для знака числа: 0 – это положительное число, 1 – отрицательное.

Если в разрядах байта с 0 по 6 поместить абсолютное значение числа, а в 7-ом бите установить его знак (0 или 1), то полученное представление числа называется прямым двоичным кодом.

Если в прямом коде число представлено как отрицательное (7-ой бит равен 1), то в числе инвертируются ¹ все разряды, кроме знакового. Такое представление числа называется обратный двоичный код.

После прибавления к обратному коду 1 получается дополнительный двоичный код.

Использование дополнительного двоичного кода позволяет создавать схемы, выполняющие вычитание, умножение и деление посредством операции сложения.

Рассмотрим на примерах операцию вычитания для 8-и битовых чисел.

ПРИМЕР 1: Вычесть число 3 из 5 (101₂ – 011₂).

• 
  Запишем абсолютное значение числа -3 в байте
  

0

0

0

0

0

0

1

1

• 
  В знаковый – седьмой – бит запишем признак отрицательности числа 1 и получим прямой двоичный код числа -3.
  

1

0

0

0

0

0

1

1

• 
  Инвертируем все разряды в числе, кроме знакового
  

1

1

1

1

1

1

0

0

Получим обратный двоичный код числа -3.

• 
  Прибавим к обратному коду единицу
  

1

1

1

1

1

1

0

1

Получим дополнительный двоичный код числа -3.

• 
  Сложим число 5 и дополнительный двоичный код числа -3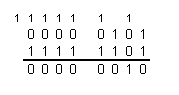
  

Получили число 010₂ = 2₁₀.

Ответ: 101₂ – 011₂ = 010₂
Проверка: Сделаем проверку, преобразуя двоичные числа к десятичному виду:

5₁₀ – 3₁₀ = 2₁₀
ПРИМЕР 2: Вычесть число 49 из 63

• 
  Прямой двоичный код числа -49
  

1

0

1

1

0

0

0

1

• 
  Инверсный код числа -49 (обратный двоичный код)
  

1

1

0

0

1

1

1

0

• 
  Дополнительный код числа -49
  

1

1

0

0

1

1

1

1

• 
  Сложим число 63 и дополнительный код числа -49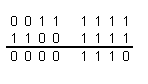
  

Получили число 1110₂ = 14₁₀

Ответ: 11 1111₂ – 11 0001₂ = 1110₂

Проверка: 63₁₀ – 49₁₀ = 14₁₀
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Используя схемы примера 1 или 2, сделайте вычитание целых чисел, используя дополнительный двоичный код.

Номер варианта	Числа	Номер варианта	Числа
1	81 и 17	9	64 и 32
2	42 и 18	10	51 и 28
3	42 и 36	11	92 и 48
4	61 и 28	12	67 и 29
5	74 и 28	13	82 и 29
6	62 и 39	14	53 и 29
7	43 и 28	15	83 и 38
8	78 и 49	16	68 и 29

Контрольные вопросы

1. 
   Что такое система счисления?
   
2. 
   Какие существуют системы счисления?
   
3. 
   Какие непозиционные системы счисления вы знаете?
   
4. 
   Приведите примеры записи чисел 467, 89011 в непозиционной системе счисления.
   
5. 
   Сформулируйте правило, как определяется величина числа в римской системе счисления?
   
6. 
   Для чего используются непозиционные системы счисления?
   
7. 
   Чем отличаются позиционные и непозиционные системы счисления?
   
8. 
   Что такое основание позиционной системы счисления?
   
9. 
   Для чего используются позиционные системы счисления?
   
10. 
    Может ли число 5 являться основанием системы счисления?
    
11. 
    Существует ли двенадцатеричная система счисления?
    
12. 
    Как математически записать любое число А в произвольной позиционной системе счисления?
    
13. 
    Что является весом разряда?
    
14. 
    Приведите пример, указав номер разряда и его вес.
    
15. 
    Сформулируйте правило, как образуются целые числа в позиционных системах счисления?
    
16. 
    Приведите пример образования трех целых чисел в шестеричной позиционной системе счисления после числа 6.
    
17. 
    Что означает понятие продвижение цифры в позиционной системе счисления?
    
18. 
    Как представляется десятичное число 8 в 16-ной, 8-ной и 2-ной системах счисления?
    
19. 
    Какие существуют достоинства и недостатки двоичной системы счисления?
    
20. 
    Что такое мощность алфавита?
    
21. 
    Правило перевода целого положительного числа из 10-ной системы счисления в любую другую позиционную систему.
    
22. 
    Как выглядит число 367₁₀ в 16-ной, 8-ной и 2-ной системах счисления?
    
23. 
    Правило перевода правильной десятичной дроби в любую другую позиционную систему.
    
24. 
    Сделайте перевод десятичной дроби 0,75 в 16-ную, 8-ную и 2-ную системы счисления.
    
25. 
    Переведите число 365,25₁₀ в 16-ную, 8-ную и 2-ную системы счисления.
    
26. 
    Правило перевода восьмеричных и шестнадцатеричных чисел в двоичную систему счисления.
    
27. 
    Переведите число 157₈ и C12₁₆ в двоичную систему счисления.
    
28. 
    Правило перевода числа из двоичной системы счисления в восьмеричную или шестнадцатеричную.
    
29. 
    Переведите число 101000011111,11001₂ в восьмеричную и шестнадцатеричную системы счисления.
    
30. 
    Применяя правило счета, составьте фрагмент таблицы сложения в восьмеричной и шестнадцатеричной системах счисления.
    
31. 
    Сложите числа 17, 6 и 5 в различных позиционных системах счисления. Сделайте проверку.
    
32. 
    Сложите числа 79,25 и 51,125 в различных позиционных системах счисления. Сделайте проверку.
    
33. 
    Найдите разность чисел 99,05 и 51,25 в различных позиционных системах счисления. Сделайте проверку.
    
34. 
    Какое представление числа называется прямым двоичным кодом? Приведите пример.
    
35. 
    Какое представление числа называется обратным двоичным кодом? Приведите пример.
    
36. 
    Что такое дополнительный двоичный код? Приведите пример.
    
37. 
    Сделайте вычитание чисел 51 и 28, используя дополнительный код.
    

Литература

1. 
   Андреева Е.В., Фалина И. Н. Системы счисления и компьютерная арифметика, Издательство: Лаборатория Базовых Знаний
   
2. 
   Андреева Е.В. Системы счисления и компьютерная арифметика. Издание 3 Бином. Лаборатория знаний
   
3. 
   Ашарина и. В. Основы программирования на языках С и С++
   
4. 
   Гашков С. Б. Системы счисления и их применение
   
5. 
   Гашков С. Б. Системы счисления и их применение
   
6. 
   Еремина Е.А. Как работает современный компьютер
   
7. 
   Касаткин В.Н. Азбука кибернетики
   

Содержание

TOC \o "1-3" \f \h \z \u 1 Непозиционные системы счисления 3

HYPERLINK \l "_Toc145178337" 2 Позиционные системы счисления PAGEREF _Toc145178337 \h 4

HYPERLINK \l "_Toc145178338" 3 Образование целых чисел в позиционных системах счисления. Правило счета. PAGEREF _Toc145178338 \h 6

HYPERLINK \l "_Toc145178339" 4 Таблица соответствия между системами счисления PAGEREF _Toc145178339 \h 8

HYPERLINK \l "_Toc145178340" 5 Правила перевода чисел из одной системы счисления в другую PAGEREF _Toc145178340 \h 10

HYPERLINK \l "_Toc145178341" 5.1 Перевод целого положительного числа из десятичной системы счисления в любую другую позиционную систему PAGEREF _Toc145178341 \h 10

HYPERLINK \l "_Toc145178342" 5.2 Перевод правильной десятичной дроби в любую другую позиционную систему счисления PAGEREF _Toc145178342 \h 12

HYPERLINK \l "_Toc145178343" 5.3 Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления PAGEREF _Toc145178343 \h 16

HYPERLINK \l "_Toc145178344" 5.4 Перевод числа из двоичной системы счисления в восьмеричную или шестнадцатеричную PAGEREF _Toc145178344 \h 17

HYPERLINK \l "_Toc145178345" 6 Арифметические операции в позиционных системах счисления PAGEREF _Toc145178345 \h 18

HYPERLINK \l "_Toc145178346" 6.1 Сложение PAGEREF _Toc145178346 \h 18

HYPERLINK \l "_Toc145178347" 6.2 Прямой, обратный и дополнительный двоичные коды PAGEREF _Toc145178347 \h 23

HYPERLINK \l "_Toc145178348" Контрольные вопросы PAGEREF _Toc145178348 \h 26

HYPERLINK \l "_Toc145178349" Литература PAGEREF _Toc145178349 \h 28

TOC \o "1-3" \f \h \z \u

1 Инверсия- замена 0 на 1, а 1 на 0

PAGE ﾵ24ﾧ