Пример решения задач по эконометрике. Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
Требуется: 1) построить уравнение множественной линейной регрессии; 2) записать модель множественной линейной регрессии; 3) оценить качество уравнения регрессии. Решение. Объем выборки n = 20, число независимых переменных (факторов) m = 3. В качестве программного средства для решения задачи воспользуемся программой «Анализ данных» в Excel, инструмент «Регрессия». Результаты расчетов представлены в табл. 2. Таблица 2
1) Уравнение множественной линейной регрессии имеет вид Используя результаты расчетов (см. табл. 2) в данном случае можно записать Коэффициент регрессии b1 = -0,003 показывает, что с увеличением цены единицы продукции на 1 руб. объем реализации продукции уменьшится на 0,003 млн руб., при условии, что расходы на рекламу останутся на прежнем уровне и организация маркетинга в организации не изменится. Коэффициент регрессии b2 = 0,013 показывает, что с увеличением расходов на рекламу на 1 тыс. руб. объем реализации продукции увеличится на 0,013 млн руб., при условии, что цена единицы продукции и организация маркетинга в организации не изменятся. Коэффициент регрессии b3 = 0,015 показывает, что организация отдела маркетинга в организации приведет к увеличению объема реализации продукции на 0,015 млн руб., при условии, что цена единицы продукции и расходы на рекламу останутся на прежнем уровне. Свободный член уравнения регрессии b0 = -0,200нельзя интерпретировать как начальный уровень объема реализации продукции, поскольку показатели «Цена единицы продукции», «Расходы на рекламу», «Отдел маркетинга в организации» не могут одновременно принимать нулевое значение. 2) Множественная линейная регрессионнаямодель зависимости объема реализации продукции от всех факторов имеет вид 3) Для проверки качества уравнения регрессии составим расчетную таблицу (см. табл. 3) (расчеты выполнены в Excel). Таблица 3 Расчетная таблица
а) Найдем среднюю относительную ошибку аппроксимации 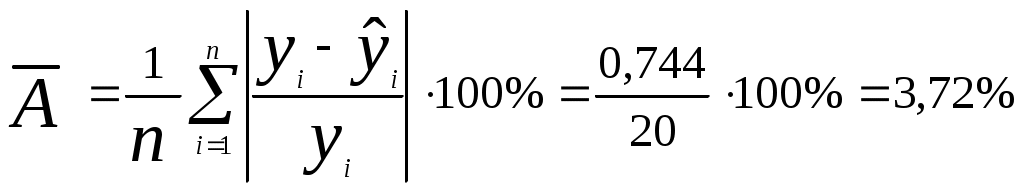 . .Так как б) Проверим статистическую значимость уравнения регрессии в целом с помощью критерия Фишера. Расчетные значения взяты из табл. 2. 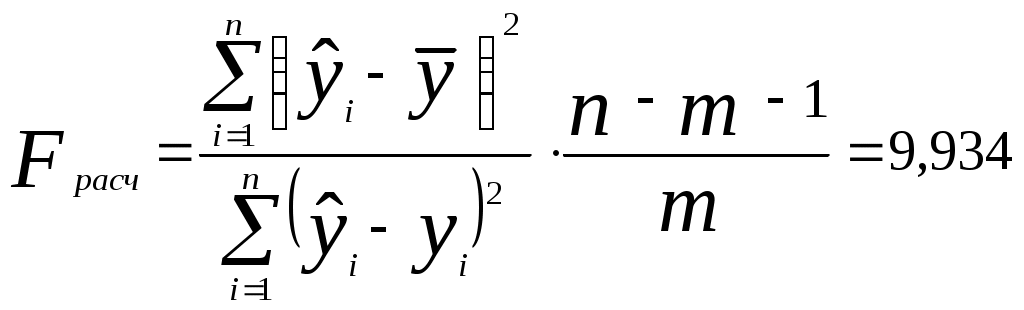 . .Табличное значение критерия Фишера с df1 = m = 3 и df2 = n - m - 1 = 20 - 3 - 1 = 16 степенями свободы при уровне значимости α = 0,05 найдем с помощью встроенной функции Excel «FРАСПОБР». Fтабл = 3,24 . Поскольку Fрасч > Fтабл , уравнение регрессии в целом статистически значимо. в) Проверим статистическую значимость параметров уравнения регрессии с помощью критерия Стьюдента. Расчетные значения взяты из табл. 2. Расчетные значения критерия равны 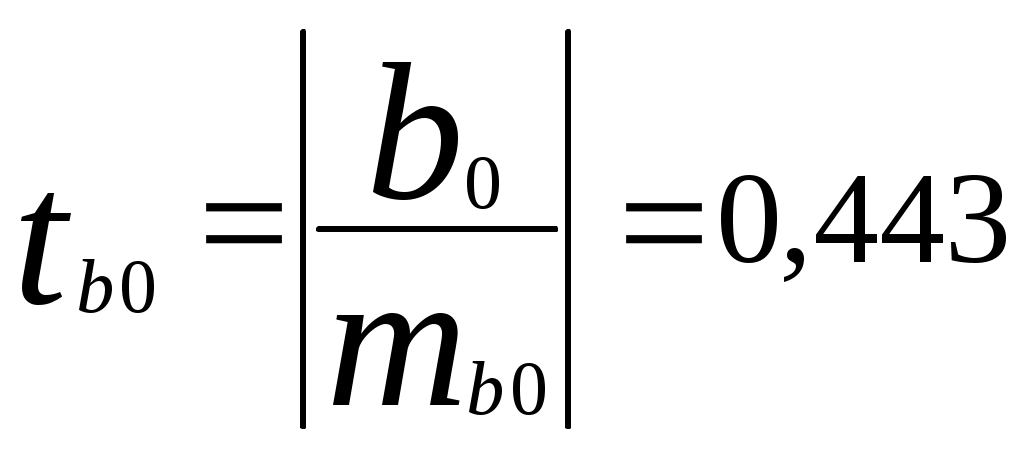 , , 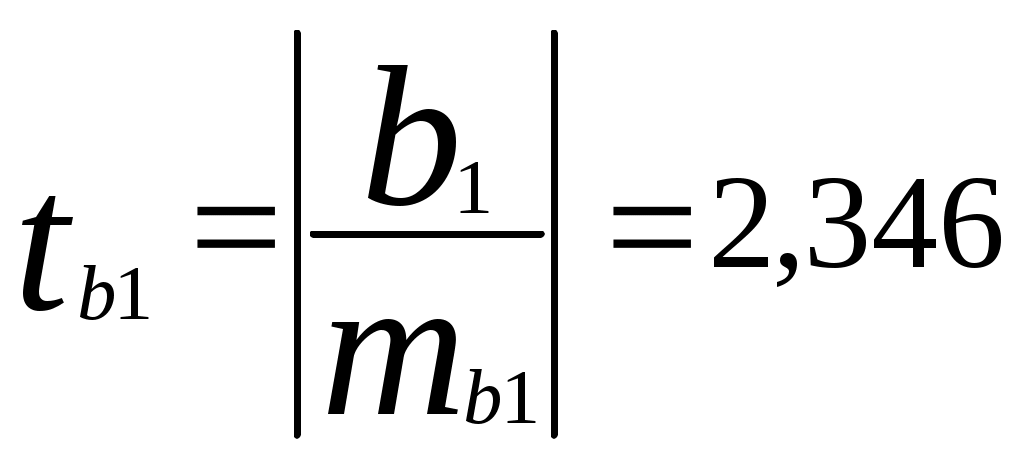 , , 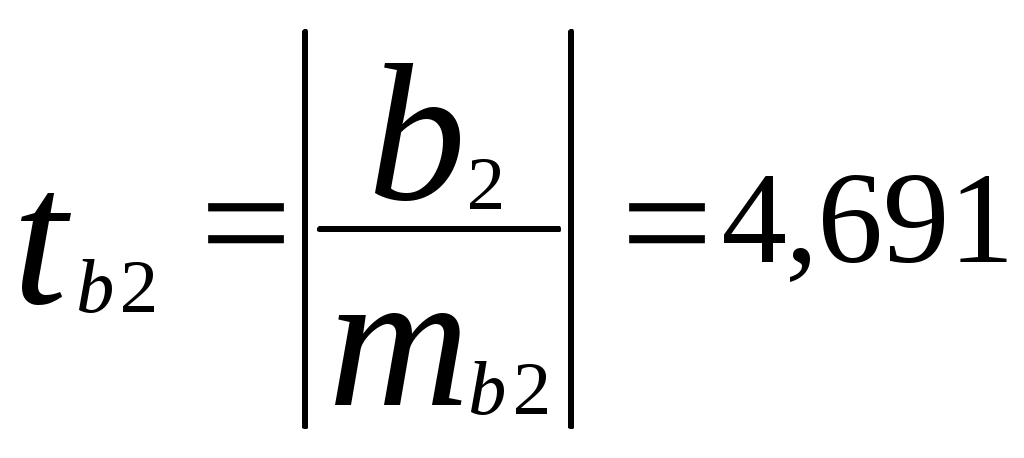 , , 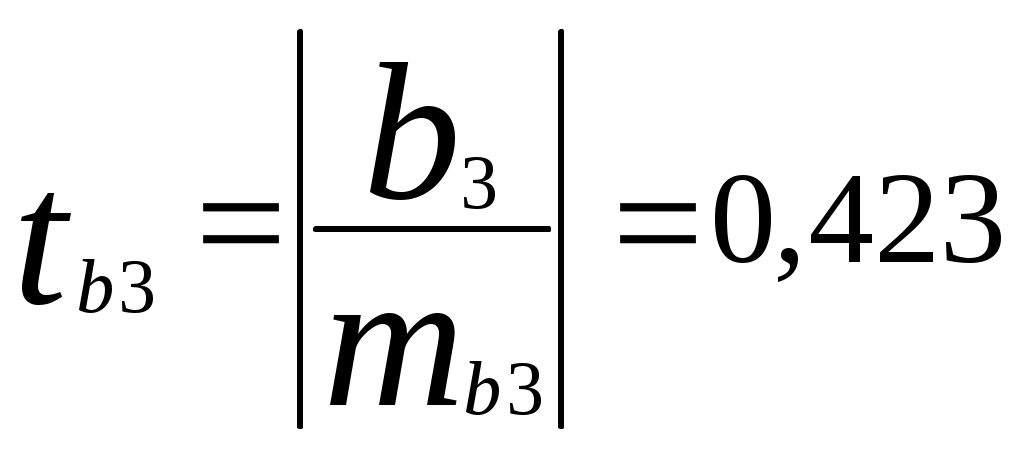 , ,где средние квадратические ошибки параметров Табличное значение t-критерия Стьюдента при уровне значимости α = 0,05 и числе степеней свободы df = n - m - 1 = 20 - 3 - 1 = 16 составляет tтабл = 2,12. (табличное значение найдено с помощью встроенной функции Excel «СТЬЮДРАСПОБР»). Так как tb0 < tтабл , параметр b0 статистически незначим; tb1 > tтабл , параметр b1 статистически значим. tb2 > tтабл , параметр b2 статистически значим. tb3 < tтабл , параметр b3 статистически незначим. г) Интервальные оценки (95%-е доверительные интервалы) параметров уравнения регрессии приведены в табл. 2: Интервальная оценка b0 : Интервальная оценка b1 : Интервальная оценка b2 : Интервальная оценка b3 : Границы доверительных интервалов для статистически незначимых параметров имеют разные знаки. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
