Пример решения задач по эконометрике. Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход

• Название: Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход
• Дата: 03.04.2020
• Размер: 1.02 Mb.
• Имя файла: Пример решения задач по эконометрике.doc
• Тип: Практикум; #114685
• страница: 11 из 11

2) Теснота нелинейной регрессионной зависимости оценивается с помощью индекса корреляции (корреляционного отношения) (необходимые здесь и далее расчеты приведены в табл. 7):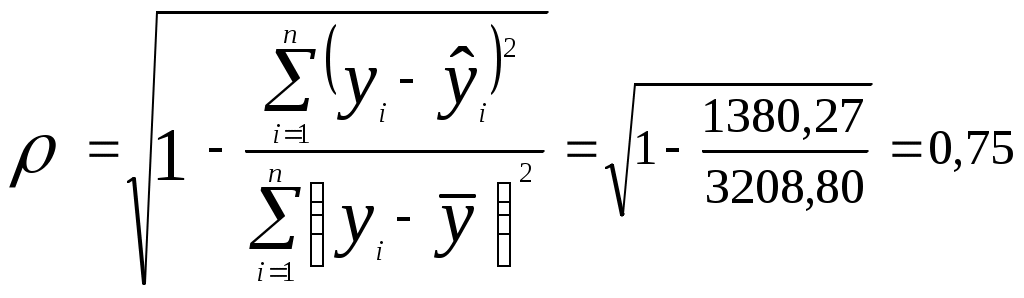

.

Значение ρ одинаково близко к 1 и к 0,5, следовательно, гиперболическая связь между процентом выполнения плана и трудовым стажем работников достаточно сильная, но близка к средней.

Коэффициент детерминации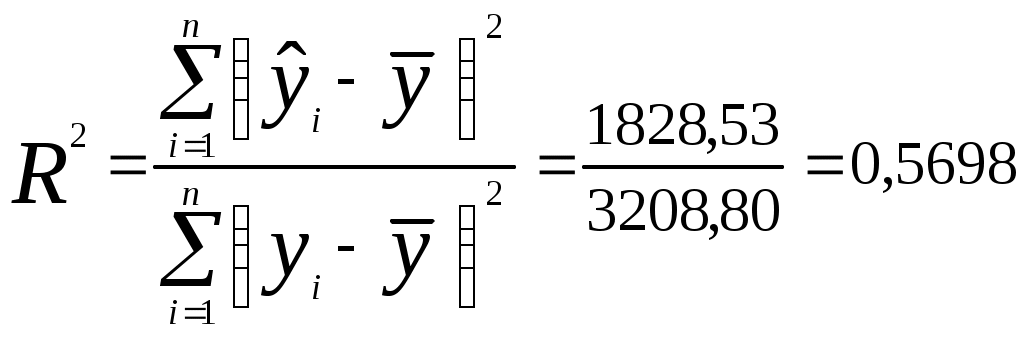



показывает, что в гиперболической модели формирование значений показателя «Процент выполнения плана» на 56,98% объясняется влиянием фактора «Трудовой стаж работника». Оставшиеся 43,02% приходятся на другие факторы, не включенные в модель.

Скорректированный коэффициент детерминации равен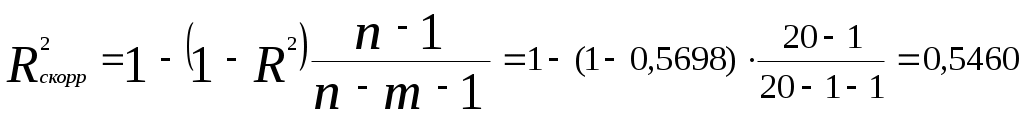



Таблица 7

Расчетная таблица характеристик гиперболической модели

№ п/п
1	1	84	90,14	0,0731	209,16	37,67	424,36	0,24
2	2	92	101,08	0,0987	12,41	82,38	158,76	0,11
3	0,5	80	68,26	0,1468	1320,60	137,83	605,16	0,64
4	2	85	101,08	0,1891	12,41	258,45	384,16	0,11
5	2,5	94	103,26	0,0986	1,78	85,83	112,36	0,08
6	3	89	104,72	0,1767	0,02	247,21	243,36	0,07
7	9	113	109,58	0,0302	24,85	11,67	70,56	0,02
8	9,5	118	109,71	0,0702	26,14	68,68	179,56	0,02
9	3,5	111	105,76	0,0472	1,36	27,41	40,96	0,06
10	4	102	106,55	0,0446	3,79	20,67	6,76	0,05
11	6	110	108,37	0,0148	14,21	2,66	29,16	0,03
12	5	102	107,64	0,0553	9,24	31,81	6,76	0,04
13	7,5	108	109,10	0,0102	20,24	1,21	11,56	0,03
14	8,5	112	109,44	0,0228	23,44	6,55	54,76	0,02
15	7	113	108,89	0,0364	18,40	16,89	70,56	0,03
16	8	115	109,28	0,0497	21,91	32,71	108,16	0,03
17	7	105	108,89	0,0370	18,40	15,13	0,16	0,03
18	11	116	110,03	0,0515	29,45	35,68	129,96	0,02
19	11	121	110,03	0,0907	29,45	120,42	268,96	0,02
20	12	122	110,19	0,0968	31,27	139,42	302,76	0,02
Сумма	120	2092	2092	1,4403	1828,53	1380,27	3208,80
Среднее	6	104,6	104,6	0,0720				0,0834

Оценим качество гиперболического уравнения регрессии;

Поскольку расчет параметров проведен верно.

а) Найдем среднюю относительную ошибку аппроксимации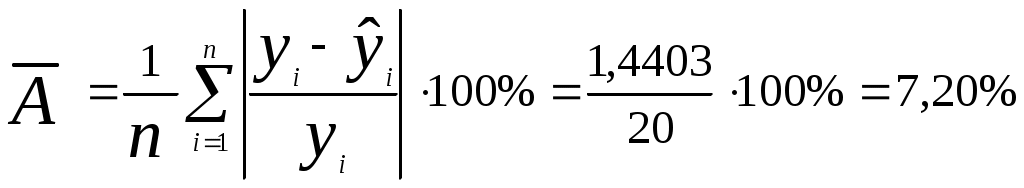

.

Так как < 10% , уравнение имеет высокую точность.

б) Проверим статистическую значимость уравнения регрессии в целом с помощью критерия Фишера. Расчетное значение (статистика) критерия Фишера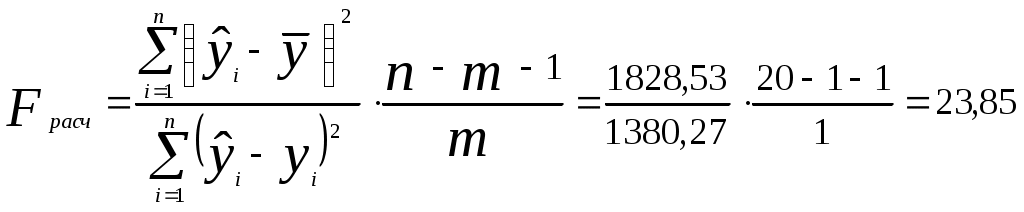

.

Табличное значение критерия Фишера с df₁ = m = 1 и df₂ = n - m - 1 = 20 -1 - 1 = 18 степенями свободы при уровне значимости α = 0,05 найдем с помощью встроенной функции Excel «FРАСПОБР». F_табл = 4,41 .

Поскольку F_расч > F_табл , уравнение показательной регрессии статистически значимо в целом, т.е. адекватно описывает исходные данные.

в) Средний и частные коэффициенты эластичности в гиперболической модели найдем по формулам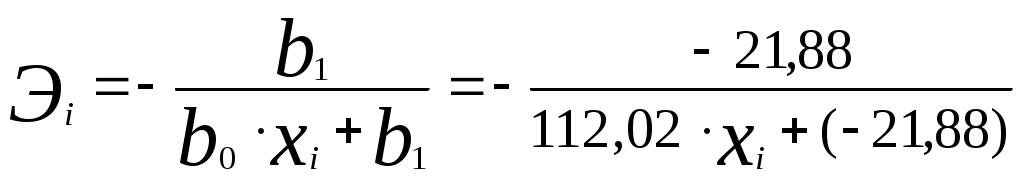





Необходимо отметить, что среднее значение, вычисленное по столбцу частных коэффициентов эластичности, не совпадает со значением среднего коэффициента эластичности (0,08 ≠ 0,03). Для анализа необходимо использовать средний коэффициент эластичности, вычисленный по формуле.

Средний коэффициент эластичности показывает, что при увеличении среднего трудового стажа работников на 1% процент выполнения плана в среднем увеличится на 0,03% (влияние трудового стажа на рост производительности труда в целом по группе наблюдений практически отсутствует).

Анализ значений частных коэффициентов эластичности показывает, что для 7, 8, 14, 18, 19 и 20-го наблюдений показатель «трудовой стаж работника» имеет наименьшее влияние на показатель «процент выполнения плана» (все частные коэффициенты эластичности равны 0,02).

Для 3-го наблюдения увеличение показателя «трудовой стаж» на 1% приводит к наибольшему увеличению процента выполнения плана, чем в целом по группе наблюдений (Э₃=0,64).

Другими словами, в рамках построенной гиперболической модели, у работников, имеющих небольшой стаж работы (два года и менее), увеличение стажа приводит к быстрому росту производительности труда. В тоже время у опытных работников, имеющих стаж работы шесть и более лет, увеличение стажа практически не приводит к росту производительности труда.
3) Выберем наилучшее из построенных уравнений.

Постоим линии регрессии на одном корреляционном поле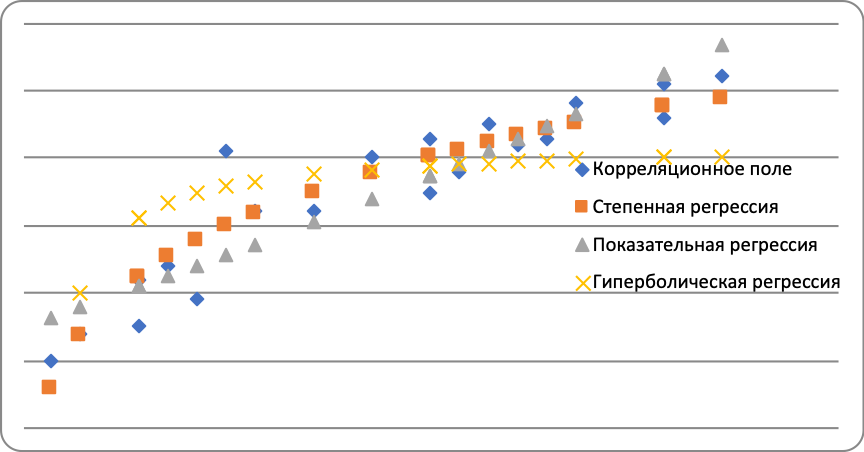



Рис. 4. Линии регрессии на корреляционном поле

Таблица 8

Характеристики регрессионных моделей

Вид регрессии	Средняя относительная ошибка аппроксимации,	Индекс корреляции,	F-статистика	Скорректированный коэффициент детерминации,
степенная	3,25	0,94	130,62	0,84
показательная	4,00	0,91	95,00	0,90
гиперболическая	7,20	0,75	23,85	0,55

Степенная модель имеет наилучшие значения модельных характеристик: наименьшую среднюю ошибку аппроксимации (наилучшая математическая точность); наибольший индекс корреляции (наиболее сильная нелинейная связь); наибольшее расчетное значение критерия Фишера (наиболее адекватное описание исходных данных). В тоже время скорректированный коэффициент детерминации для нее меньше, чем для показательной модели. Несмотря на то, что формально наилучшая модель выбирается по наибольшему значению скорректированного коэффициента детерминации, в данном случае будем считать наилучшей степенную модель, поскольку она правильнее отражает закономерность в исходных данных, отраженную на корреляционном поле (см. рис. 4)

Для практического применения следует использовать выводы о степени влияния трудового стажа на процент выполнения плана, сделанные по коэффициентам эластичности, которые вычислены для степенной модели.