Пример решения задач по эконометрике. Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
Решение. Объем выборки n = 20. 1) Выборочный парный коэффициент корреляции между переменными u и v можно определить по формуле: 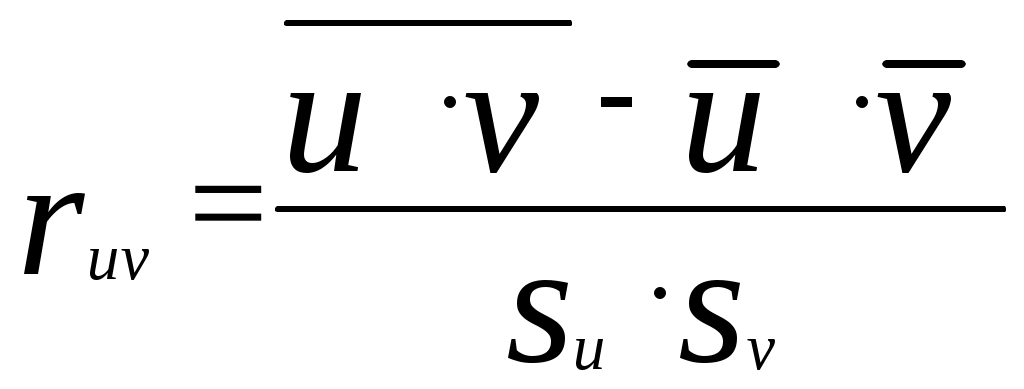 , , где среднеквадратические отклонения переменных Для получения матрицы парных коэффициентов корреляции проведем расчеты (см. табл. 4). Таблица 4 Расчетная таблица
В результате получим: и 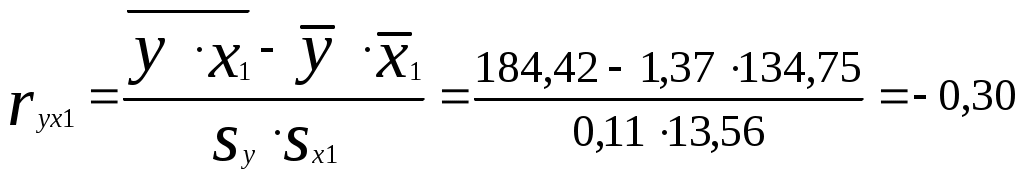 ; ;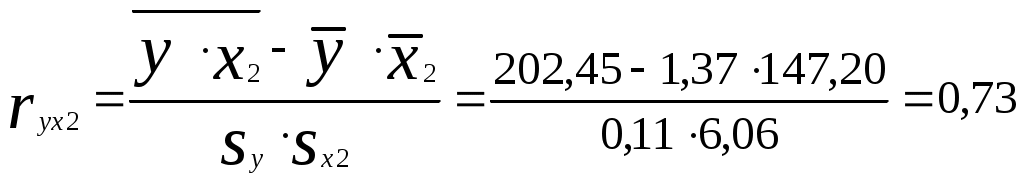 ; ;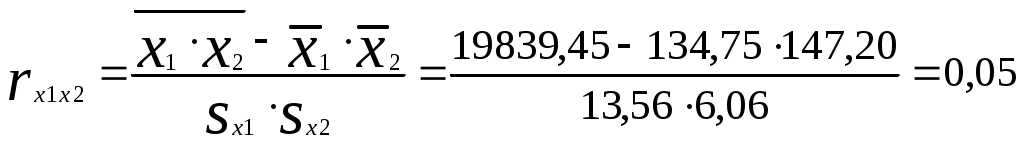 . .Матрица выборочных парных коэффициентов корреляции (корреляционная матрица) имеет вид 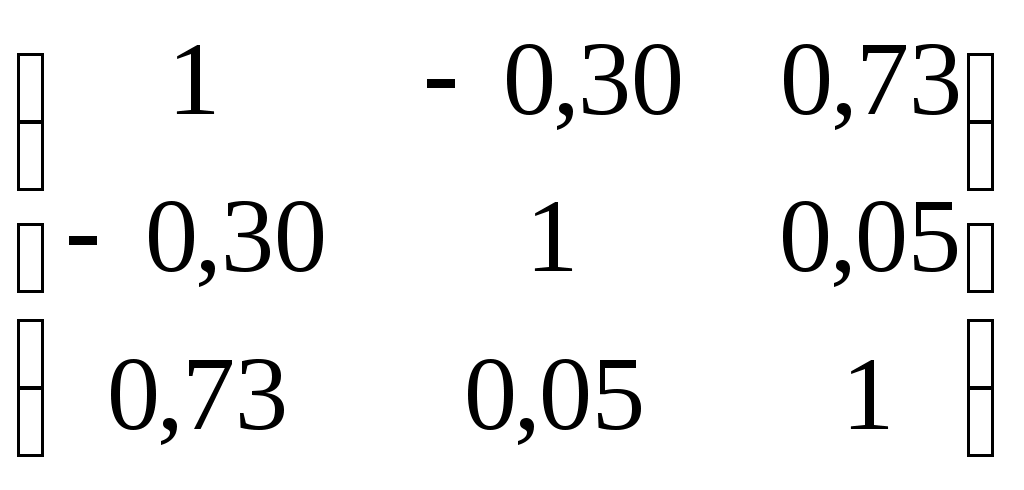 . .На основе корреляционной матрицы можно сделать вывод о том, что для данной группы торговых организаций между объемом реализации продукции и ее ценой существует прямая сильная связь; связь между объемом реализации продукции и расходами на рекламу - обратная слабая; между расходами на рекламу и ценой продукции связь практически отсутствует. 2) Корреляционная матрица является основой для вычисления частных коэффициентов корреляции. В трехмерном случае частный коэффициент корреляции между случайными величинами u и v при фиксированном значении третьей величины w определяется по формуле:  . .Частный коэффициент корреляции между y и x1 при фиксированном x2 равен 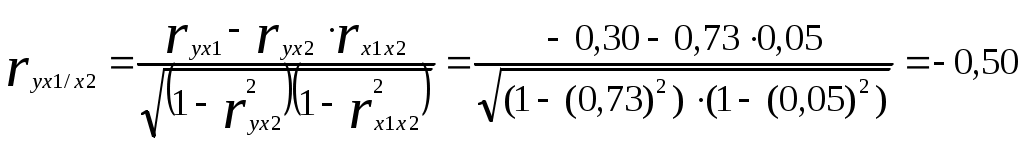 . .Поскольку по абсолютной величине парный коэффициент корреляции (ryx1 = ‑0,30) меньше частного коэффициента корреляции (ryx1/x2 = -0,50) наличие третьей переменной (х2) усиливает связь между y и x1 . Другими словами, фиксирование цены продукции усиливает зависимость объема реализации продукции от расходов на рекламу. Частный коэффициент корреляции между y и x2 при фиксированном x1 равен 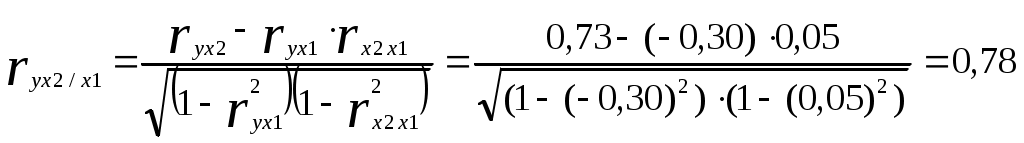 Поскольку парный коэффициент корреляции (ryx2 = 0,73) меньше частного коэффициента корреляции (ryx2/x1 = 0,78) наличие третьей переменной (х1) усиливает связь между y и x2 . Другими словами, фиксирование расходов на рекламу усиливает зависимость объема реализации продукции от ее цены. 3) На основе корреляционной матрицы вычислим выборочный множественный коэффициент корреляции между y и х1, х2 и коэффициент детерминации. 1. Способ. Воспользуемся формулой:  Коэффициент детерминации равен 2. Способ. Найдем коэффициент детерминации по формуле 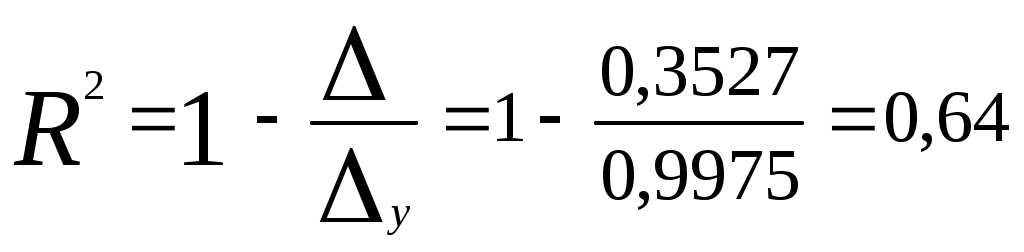 , , где определитель корреляционной матрицы 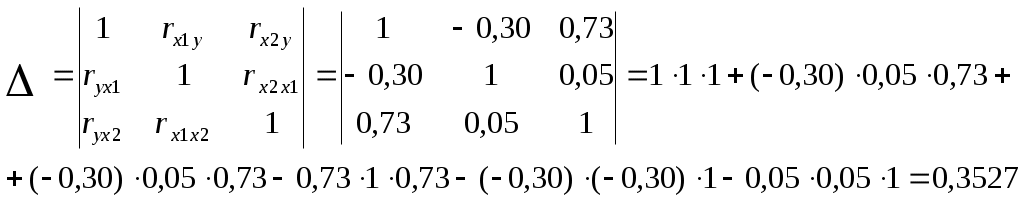 , ,определитель матрицы межфакторных корреляций Коэффициент множественной корреляции Проверим статистическую значимость коэффициента множественной корреляции с помощью критерия Фишера (m = 2). Найдем 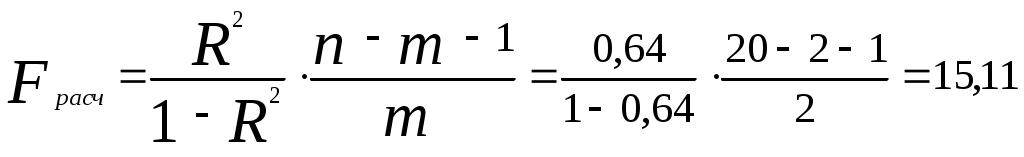 Табличное значение F-критерия Фишера при уровне значимости α = 0,05 и числах степеней свободы df1 = m = 2 и df2 = n - m - 1 = 20 - 2 - 1 = 17 составляет Fтабл = 3,59. (табличное значение критерия найдено с помощью встроенной функции Excel «FРАСПОБР»). Так как Fрасч > Fтабл (15,11 > 3,59), коэффициент множественной корреляции признается статистически значимым. Значение коэффициента множественной корреляции показывает, что между объемом реализации продукции и расходами на рекламу, а также ценой продукции существует сильная связь. При этом расходы на рекламу и цена продукции на 64% объясняет изменение объема реализации продукции. Остальные 36% объясняются другими факторами, не включенными в модель. Задача 3.1. Имеются выборочные данные (табл. 1) показателей «среднедушевой денежный доход» (х, руб.) и «среднедушевой оборот розничной торговли» (y, руб.). Таблица 1
|
