Пример решения задач по эконометрике. Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход
 Скачать 1.02 Mb.
|
|
Оценим качество степенного уравнения регрессии; Поскольку  расчет параметров проведен верно.а) Найдем среднюю относительную ошибку аппроксимации 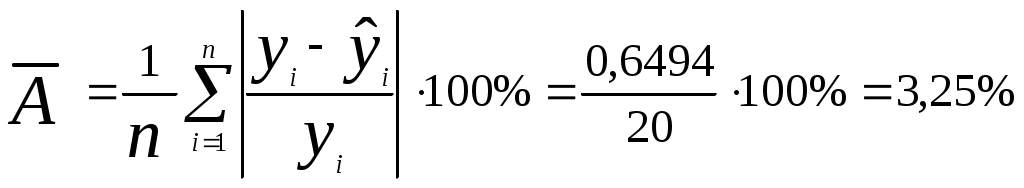 .Так как  < 10% , уравнение имеет высокую точность.б) Проверим статистическую значимость уравнения регрессии в целом с помощью критерия Фишера. Расчетное значение (статистика) критерия Фишера 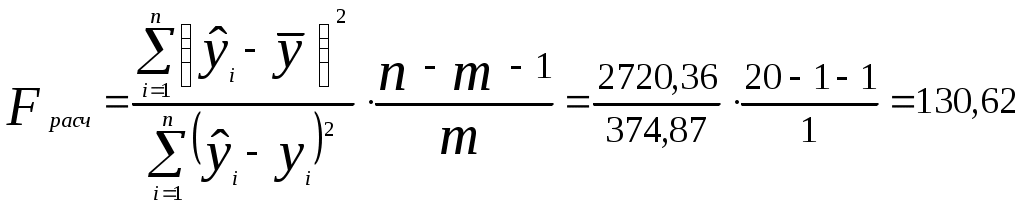 .Табличное значение критерия Фишера с df1 = m = 1 и df2 = n - m - 1 = 20 -1 - 1 = 18 степенями свободы при уровне значимости α = 0,05 найдем с помощью встроенной функции Excel «FРАСПОБР». Fтабл = 4,41 . Поскольку Fрасч > Fтабл , уравнение степенной регрессии статистически значимо в целом, т.е. адекватно описывает исходные данные. в) Средний и частные коэффициенты эластичности в степенной модели  ,  ,постоянные и равны b1 = 0,14, т.е. при увеличении трудового стажа работника на 1% процент выполнения плана увеличится на 0,14%. Показательная регрессия 1) Для нахождения параметров b0, b1 уравнения показательной регрессии  приведем уравнение к линейному виду. Введем новые переменные  ,  ,  .Тогда уравнение регрессии примет вид  .Параметры уравнения определим по формулам (необходимые расчеты приведены в табл. 4): 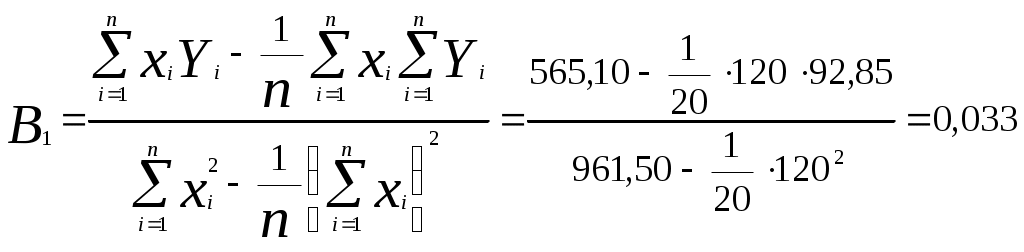 , .Обратный переход к параметру b0 осуществим по формуле   .Уравнение показательной регрессии имеет вид  .Показательная регрессионная модель имеет вид  или  Подставляя в полученное уравнение регрессии значения 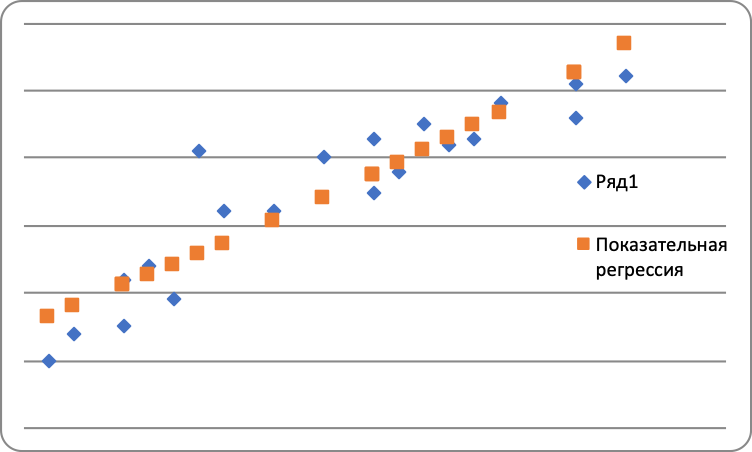 можно определить теоретические значения  и построить линию регрессии на корреляционном поле (рис. 2). Рис. 2. Линия показательной регрессии на корреляционном поле Линия показательной регрессии проходит внутри корреляционного поля. Кроме того, число точек корреляционного поля (9), лежащих выше линии регрессии, примерно равно числу точек (11), лежащих ниже линии регрессии. Следовательно, линия показательной регрессии занимает правильное положение. Таблица 4 Расчетная таблица параметров уравнения показательной регрессии
|
