Пример решения задач по эконометрике. Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход

• Название: Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход
• Дата: 03.04.2020
• Размер: 1.02 Mb.
• Имя файла: Пример решения задач по эконометрике.doc
• Тип: Практикум; #114685
• страница: 4 из 11

Средние значения признаков равны





Коэффициент парной корреляции равен

.

Статистическую значимость коэффициента корреляции проверим с помощью критерия Стьюдента. Найдем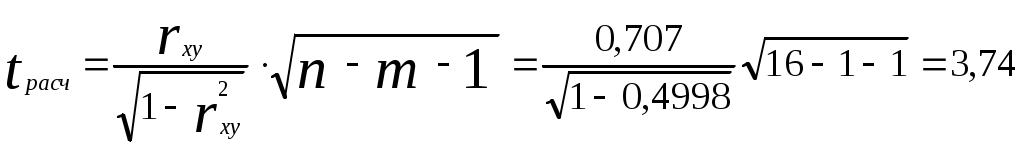

(m = 1).

Табличное значение t-критерия Стьюдента при уровне значимости α = 0,05 и числе степеней свободы df = n - m - 1 = 16 - 1 - 1 = 14 составляет t_табл = 2,14. ( табличное значение найдено с помощью встроенной функции Excel «СТЬЮДРАСПОБР»).

Так как |t_расч| > t_табл (3,74 > 2,14) , значение коэффициента корреляции статистически значимо.

Величина статистически значимого коэффициента парной корреляции свидетельствует о тесной линейной связи (близкой к умеренной) между среднедушевым денежным доходом и среднедушевым оборотом розничной торговли.

Коэффициент детерминации



Показывает, что на 49,98% изменение оборота розничной торговли объясняется изменениями денежных доходов населения. Оставшиеся 50,02% приходятся на другие факторы, не включенные в модель.

Построение уравнения парной линейной регрессии теоретически обосновано.

2) Уравнение парной линейной регрессии

найдем методом наименьших квадратов по формулам, предварительно проведя необходимые расчеты (здесь и далее см. табл. 3):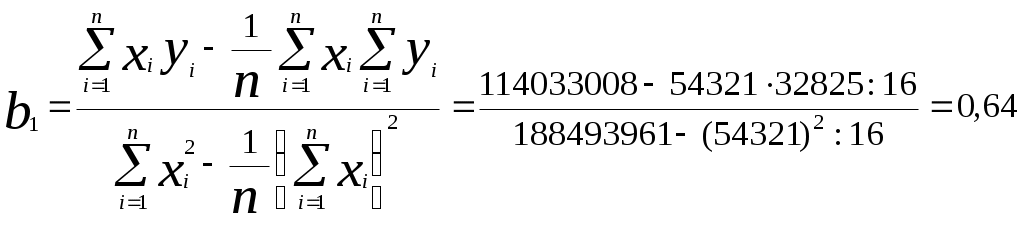

,



Уравнение парной линейной регрессии имеет вид:

.

Коэффициент регрессии b₁ = 0,64 показывает, что с увеличением среднедушевого денежного дохода на 1 руб. среднедушевой розничный оборот возрастает на 63 коп.

Подставляя в полученное уравнение регрессии значения можно определить теоретические значения .

Таблица 3

Расчетная таблица

% п/п
1	3357	2425	11269449	8140725	2027,3	0,164	586,5	158129,7	1448,8
2	3135	2050	9828225	6426750	1886,1	0,080	27379,7	26865,1	67632,5
3	2842	1683	8076964	4783086	1699,7	0,010	123828,9	277,9	305878,1
4	3991	2375	15928081	9478625	2430,7	0,023	143772,2	3106,5	355141,5
5	2293	1167	5257849	2675931	1350,4	0,157	491683,9	33621,2	1214541,8
6	3563	2200	12694969	7838600	2158,4	0,019	11417,4	1729,3	28203,0
7	3219	1892	10361961	6090348	1939,5	0,025	12548,9	2260,1	30998,0
8	3308	2008	10942864	6642464	1996,2	0,006	3068,6	140,0	7579,9
9	3724	2225	13868176	8285900	2260,9	0,016	43802,6	1285,5	108199,9
10	3416	1983	11669056	6773928	2064,9	0,041	177,5	6705,0	438,4
11	3340	1925	11155600	6429500	2016,5	0,048	1227,4	8377,4	3031,9
12	3089	1042	9541921	3218738	1856,8	0,782	37922,2	663941,8	93674,3
13	4372	2925	19114384	12788100	2673,2	0,086	386373,3	63427,5	954406,9
14	3022	2342	9132484	7077524	1814,2	0,225	56342,6	278576,4	139175,6
15	3383	2458	11444689	8315414	2043,9	0,168	58,9	171489,1	145,5
16	4267	2125	18207289	9067375	2606,3	0,227	307782,7	231692,2	760275,0
Сумма	54321	32825	188493961	114033008	32825,0	2,078	1647973,3	1651624,6	4070770,9
Среднее	3395,1	2051,6			2051,6	0,1299

3) Модель парной линейной регрессии имеет вид



или


4) Оценим качество уравнения регрессии;

а) Найдем среднюю относительную ошибку аппроксимации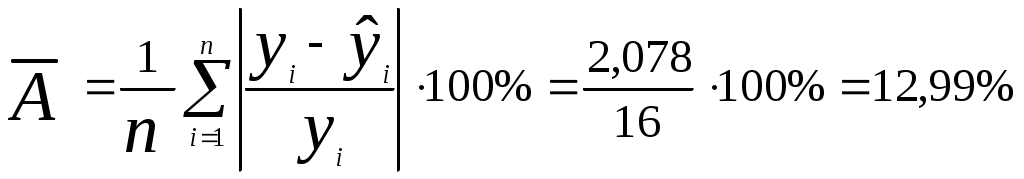

.

Так как 10% < < 20% , уравнение имеет хорошую точность.

б) Проверим статистическую значимость уравнения регрессии в целом с помощью критерия Фишера. Необходимые расчеты приведены в табл. 3.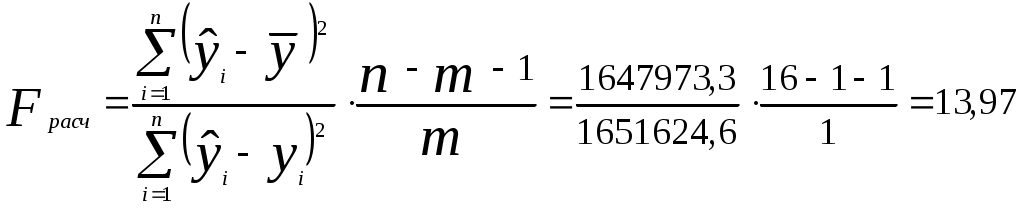

.

Табличное значение критерия Фишера с df₁ = m = 1 и df₂ = n - m - 1 = 16 -1 - 1 = 14 степенями свободы при уровне значимости α = 0,05 найдем с помощью встроенной функции Excel «FРАСПОБР». F_табл = 4,60 .

Поскольку F_расч > F_табл , уравнение регрессии статистически значимо в целом.

в) Проверим статистическую значимость параметров уравнения регрессии с помощью критерия Стьюдента. Необходимые расчеты приведены в табл. 3.

Расчетные значения критерия равны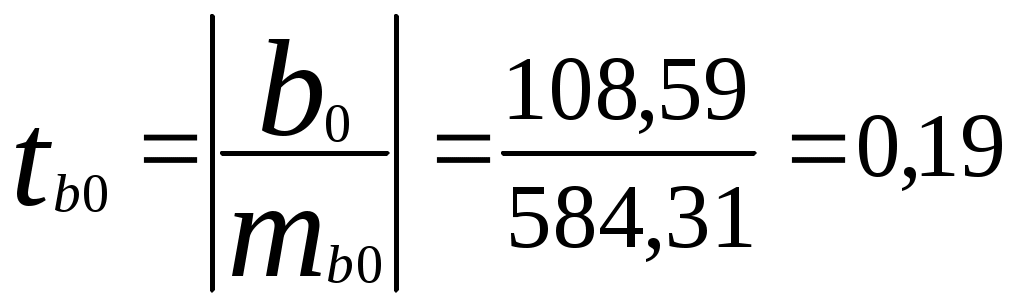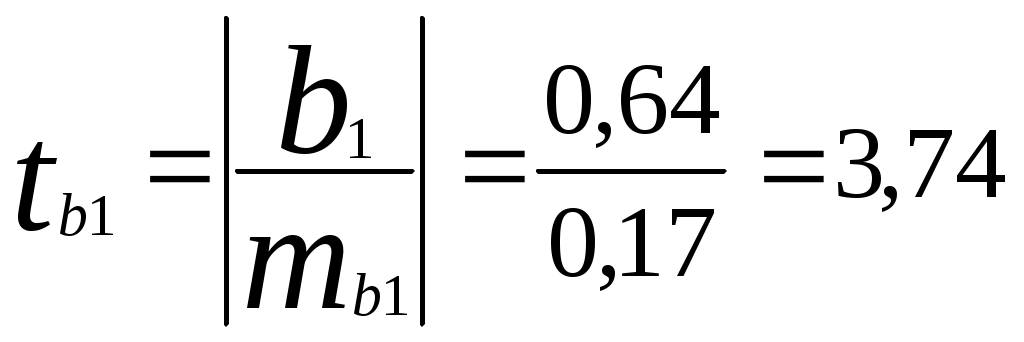

,
.

Средние квадратические ошибки параметров равны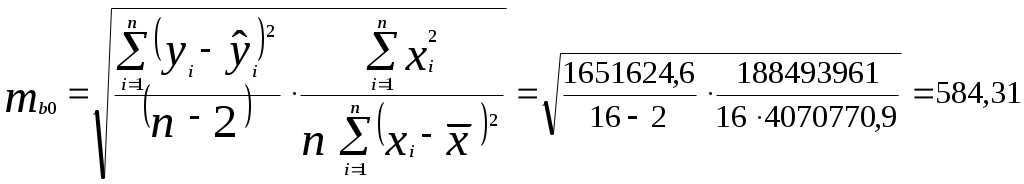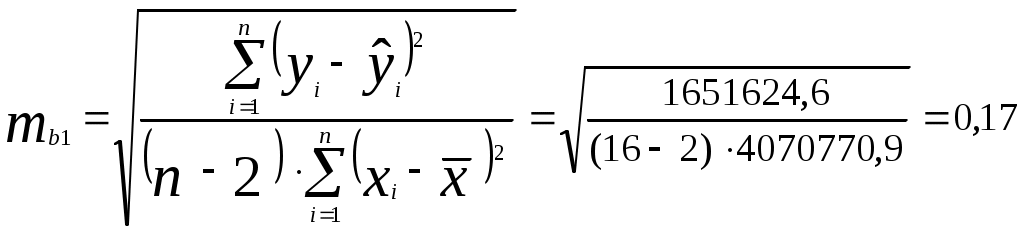

,
.

Табличное значение критерия Стьюдента t_табл = 2,14 найдено в пункте 1).

Так как t_b0 < t_табл , параметр b₀ статистически незначим; t_b1 > t_табл , параметр b₁ статистически значим.

г) Найдем интервальные оценки параметров по формулам:

;

;

;

.

Интервальная оценка b₀ : .

Интервальная оценка b₁ : .
Задача 4.1. Имеются выборочные данные (табл. 1) показателей «Объем реализации продукции» (y, млн руб.), «Цена единицы продукции» (х₁, руб.), «Расходы на рекламу» (х₂, тыс. руб.), «Отдел маркетинга в организации» (х₃, 1 - есть, 0 - нет, ).

Таблица 1

Исходные данные

№ организации	Объем реализации продукции (y)	Цена единицы продукции (x1)	Расходы на рекламу (x2)	Отдел маркетинга в организации (x3)
1	1,27	138	140	1
2	1,34	134	141	1
3	1,25	116	136	0
4	1,28	137	149	1
5	1,43	127	154	0
6	1,25	125	143	0
7	1,53	116	155	1
8	1,57	134	155	1
9	1,27	145	151	1
10	1,46	135	154	1
11	1,28	164	147	0
12	1,55	109	151	0
13	1,35	145	144	0
14	1,49	144	156	1
15	1,46	132	152	0
16	1,25	122	141	0
17	1,29	163	148	1
18	1,28	139	141	1
19	1,33	134	139	0
20	1,51	136	147	1