Пример решения задач по эконометрике. Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход
 Скачать 1.02 Mb.
|
|
Оценим качество показательного уравнения регрессии; Поскольку  расчет параметров проведен верно.а) Найдем среднюю относительную ошибку аппроксимации 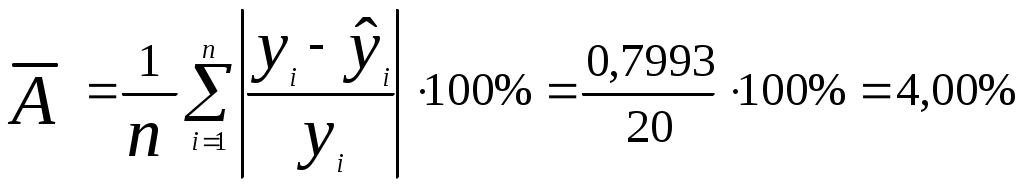 .Так как  < 10% , уравнение имеет высокую точность.б) Проверим статистическую значимость уравнения регрессии в целом с помощью критерия Фишера. Расчетное значение (статистика) критерия Фишера 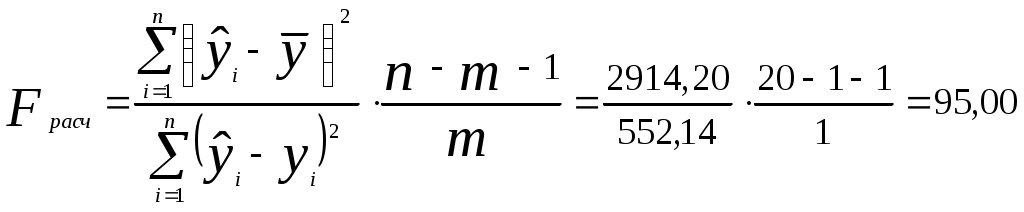 .Табличное значение критерия Фишера с df1 = m = 1 и df2 = n - m - 1 = 20 -1 - 1 = 18 степенями свободы при уровне значимости α = 0,05 найдем с помощью встроенной функции Excel «FРАСПОБР». Fтабл = 4,41 . Поскольку Fрасч > Fтабл , уравнение показательной регрессии статистически значимо в целом, т.е. адекватно описывает исходные данные. в) Средний и частные коэффициенты эластичности в показательной модели найдем по формулам   Средний коэффициент эластичности показывает, что при увеличении среднего трудового стажа работников на 1% процент выполнения плана в среднем увеличится на 0,20%. Анализ значений частных коэффициентов эластичности показывает, что для 1-го и 3-го наблюдения показатель «трудовой стаж работника» практически не влияет на показатель «процент выполнения плана» (Э1=0,03, Э3=0,02)(для данных наблюдений влияние x на y наименьшее). Для 18-го, 19-го и 20-го наблюдений увеличение показателя «трудовой стаж» на 1% приводит к наибольшему увеличению процента выполнения плана, чем в целом по группе наблюдений (Э18=0,36, Э19=0,36, Э20=0,40) (для данных наблюдений влияние x на y наибольшее). Другими словами, в рамках построенной показательной модели, у работников, имеющих небольшой стаж работы, менее трех лет, увеличение стажа практически не приводит к росту производительности труда. В тоже время у опытных работников, имеющих стаж работы более десяти лет, увеличение стажа приводит к значительно большему росту производительности труда. Необходимо отметить, что среднее значение, вычисленное по столбцу частных коэффициентов эластичности, как правило, не совпадает со значением среднего коэффициента эластичности. Для анализа необходимо использовать средний коэффициент эластичности, вычисленный по формуле. Гиперболическая регрессия 1) Для нахождения параметров b0, b1 уравнения гиперболической регрессии 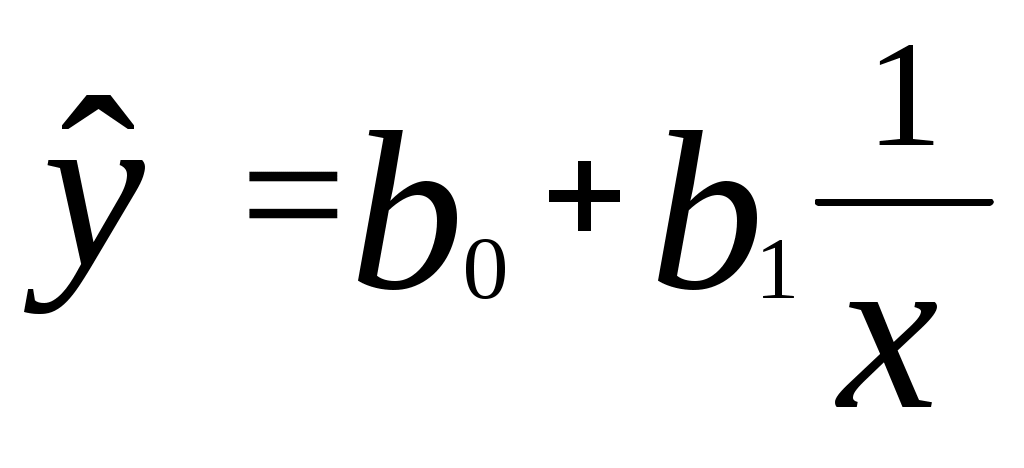 приведем уравнение к линейному виду. Введем новую переменную 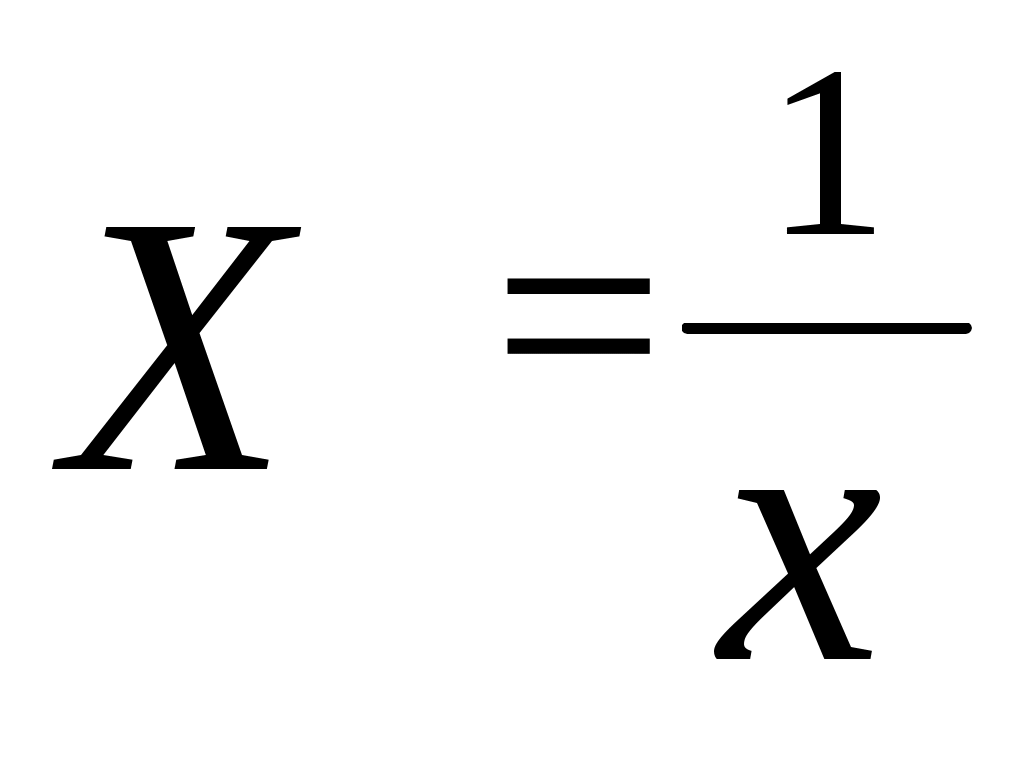 .Тогда уравнение регрессии примет вид  .Параметры уравнения определим по формулам (необходимые расчеты приведены в табл. 6): 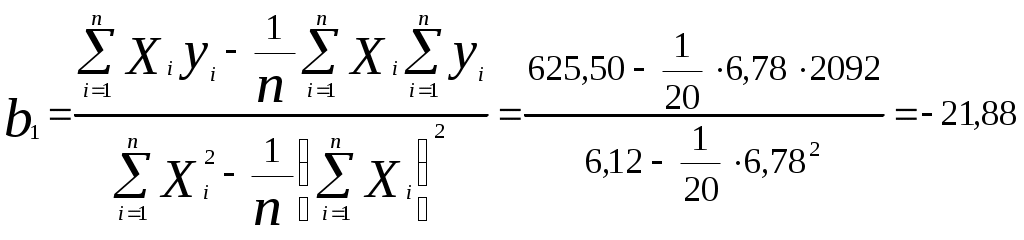 , .Уравнение гиперболической регрессии имеет вид  .Гиперболическая регрессионная модель имеет вид  или  Подставляя в полученное уравнение регрессии значения 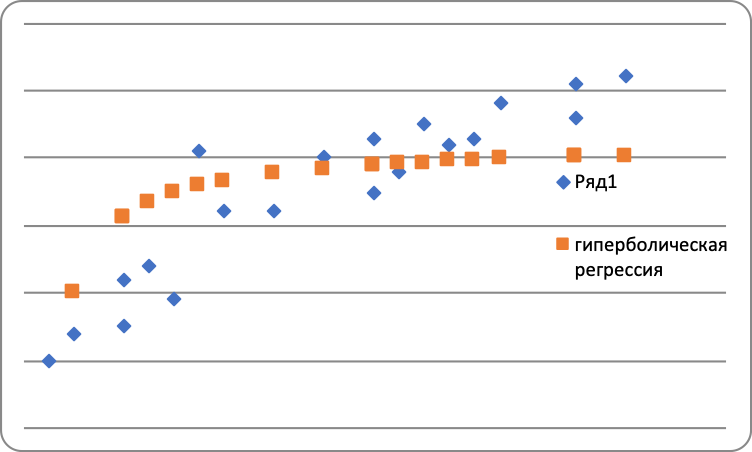 можно определить теоретические значения  и построить линию регрессии на корреляционном поле (рис. 3). Рис. 3. Линия гиперболической регрессии на корреляционном поле Линия показательной регрессии проходит внутри корреляционного поля. Кроме того, число точек корреляционного поля (10), лежащих выше линии регрессии, примерно равно числу точек (10), лежащих ниже линии регрессии. Следовательно, линия регрессии занимает правильное положение. Таблица 6 Расчетная таблица параметров уравнения гиперболической регрессии
|
