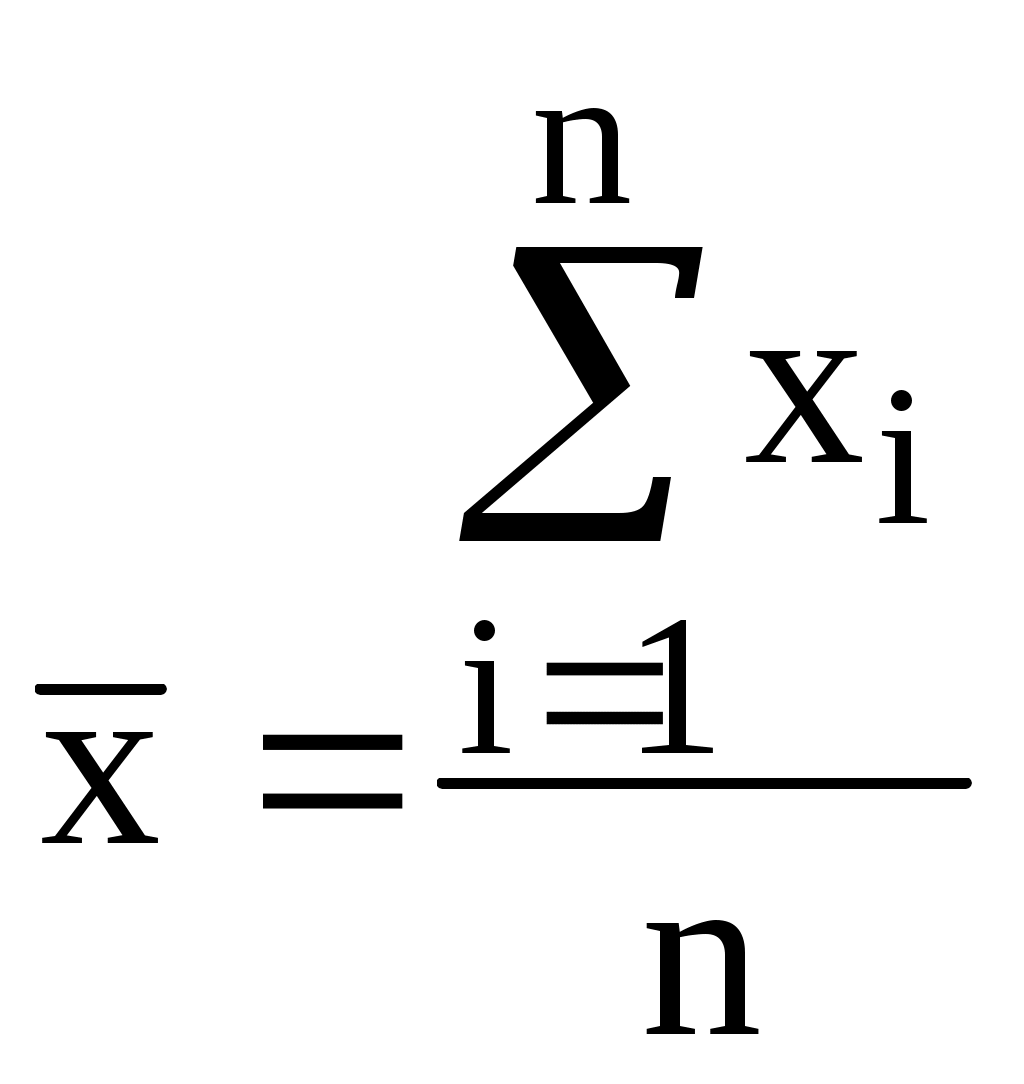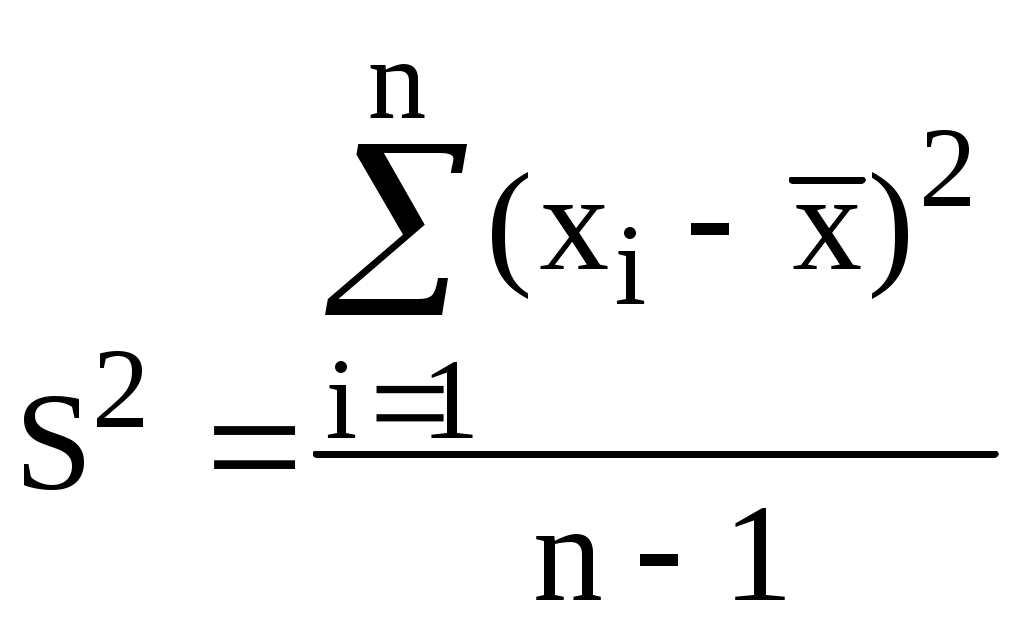Аналитическая химия. !курс лекций 5 семестр. Предмет аналитической химии

• Название: Предмет аналитической химии
• Анкор: Аналитическая химия
• Дата: 15.05.2023
• Размер: 4.18 Mb.
• Имя файла: !курс лекций 5 семестр.doc
• Тип: Документы; #1131241
• страница: 14 из 15

Метод градуировочного графика

При использовании данного метода готовится серия стандартных растворов с разными концентрациями вещества, которые считаются точно известными. Затем для каждого приготовленного раствора в одинаковых условиях получают соответствующую величину аналитического сигнала (рис. 10.1).

Для получения градуировочных графиков иногда используют внутренние стандарты - компоненты, содержание которых во всех пробах, используемых для построения градуировочного графика, и в анализируемой пробе одинаково (они могут содержаться в исходной пробе или специально в неё добавляться). В качестве аналитического сигнала в случае использования внутреннего стандарта используют отношение y/y_вс.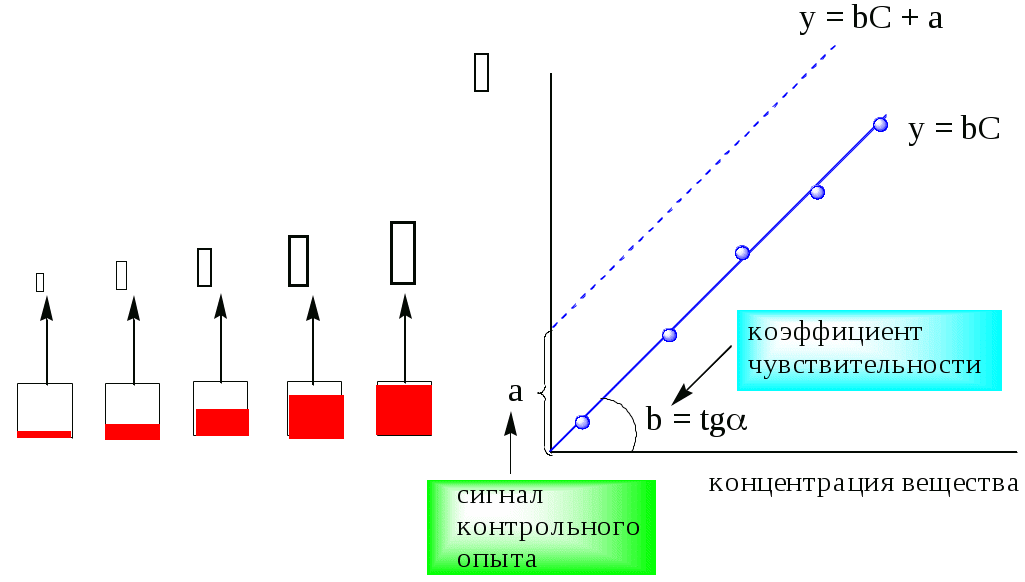


Рис. 10.1. Построение градуировочного графика и его основные параметры

Уравнения, описывающие градуировочный график, можно получить методом наименьших квадратов: коэффициенты a и b должны быть такими, чтобы сумма квадратов отклонений реальных значений от рассчитанных по полученному уравнению была бы минимальной. Согласно методу наименьших квадратов коэффициенты b и a рассчитываются по следующим формулам:

градуировочный график не проходит через начало координат



градуировочный график проходит через начало координат



«Качество» полученного градуировочного графика можно охарактеризовать коэффициентом корреляции (r). Чем ближе его значение к 1, чем меньше разброс точек относительно полученной прямой. Для практических целей рекомендуется использовать градуировочные графики c r > 0,99.

Градуировочный график желательно строить в таком интервале, чтобы неизвестная концентрация вещества попадала примерно в его середину, так как погрешность при этом будет минимальной.

Пример 10.1. При измерении оптической плотности растворов с известной концентрацией растворённого вещества были получены следующие значения:

С, мг/л	1,00	3,00	5,00	7,00	9,00
A	0,125	0,350	0,570	0,795	1,010

Раствор с неизвестной концентрацией вещества имел оптическую плотность 0,500. Определить концентрацию вещества в данном растворе.

Методом наименьших квадратов можно определить, что

A = 0,111C + 0,016 (r = 0,999)

Для расчётов удобнее использовать обратное уравнение градуировочного графика, характеризующего зависимость концентрации от оптической плотности. Для данного случая

C = 9,03A - 0,15

Концентрация вещества в исследуемом растворе равна 4,37 мг/л.

Метод стандартов

В методе одного стандартного раствора измеряют величину аналитического сигнала (y_ст) для раствора с известной концентрацией вещества (C_ст). Затем измеряют величину аналитического сигнала (y_x) для раствора с неизвестной концентрацией вещества (С_x).



Такой способ расчёта можно использовать в том случае, если зависимость аналитического сигнала от концентрации описывается линейным уравнением без свободного члена. Концентрация вещества в стандартном растворе должна быть такой, чтобы величины аналитических сигналов, полученных при использовании стандартного раствора и раствора с неизвестной концентрацией вещества, были бы как можно ближе друг к другу.

В методе двух стандартных растворов измеряют величины аналитических сигналов для стандартных растворов с двумя разными концентрацией вещества, одна из которых (C₁) меньше предполагаемой неизвестной концентрации (C_x), а вторая (C₂) - больше.

или

Метод двух стандартных растворов используют, если зависимость аналитического сигнала от концентрации описывается линейным уравнением, не проходящим через начало координат.

Пример 10.2. Для определения неизвестной концентрации вещества были использованы два стандартных раствора: концентрация вещества в первом из них равна 0,50 мг/л, а во втором - 1,50 мг/л. Оптические плотности данных растворов составили, соответственно, 0,200 и 0,400. Чему равна концентрация вещества в растворе, оптическая плотность которого составляет 0,280?

= 0,90 мг/л

Метод добавок

Метод добавок обычно используется при анализе сложных матриц, когда матричные компоненты оказывают влияние на величину аналитического сигнала и невозможно точно скопировать матричный состав образца. Данный метод может быть использован лишь в том случае, когда градуировочный график является линейным и проходит через начало координат.

При использовании расчётного метода добавок вначале измеряют величину аналитического сигнала для пробы с неизвестной концентрацией вещества (y_x). Затем к данной пробе прибавляют некоторое точное количество определяемого вещества и снова измеряют величину аналитического сигнала (y_доб).



Если необходимо учесть разбавление раствора



Пример 10.3. Исходный раствор с неизвестной концентрацией вещества имел оптическую плотность 0,200. После того, как к 10,0 мл этого раствора добавили 5,0 мл раствора с концентрацией этого же вещества 2,0 мг/л, оптическая плотность раствора стала равной 0,400. Определите концентрацию вещества в исходном растворе.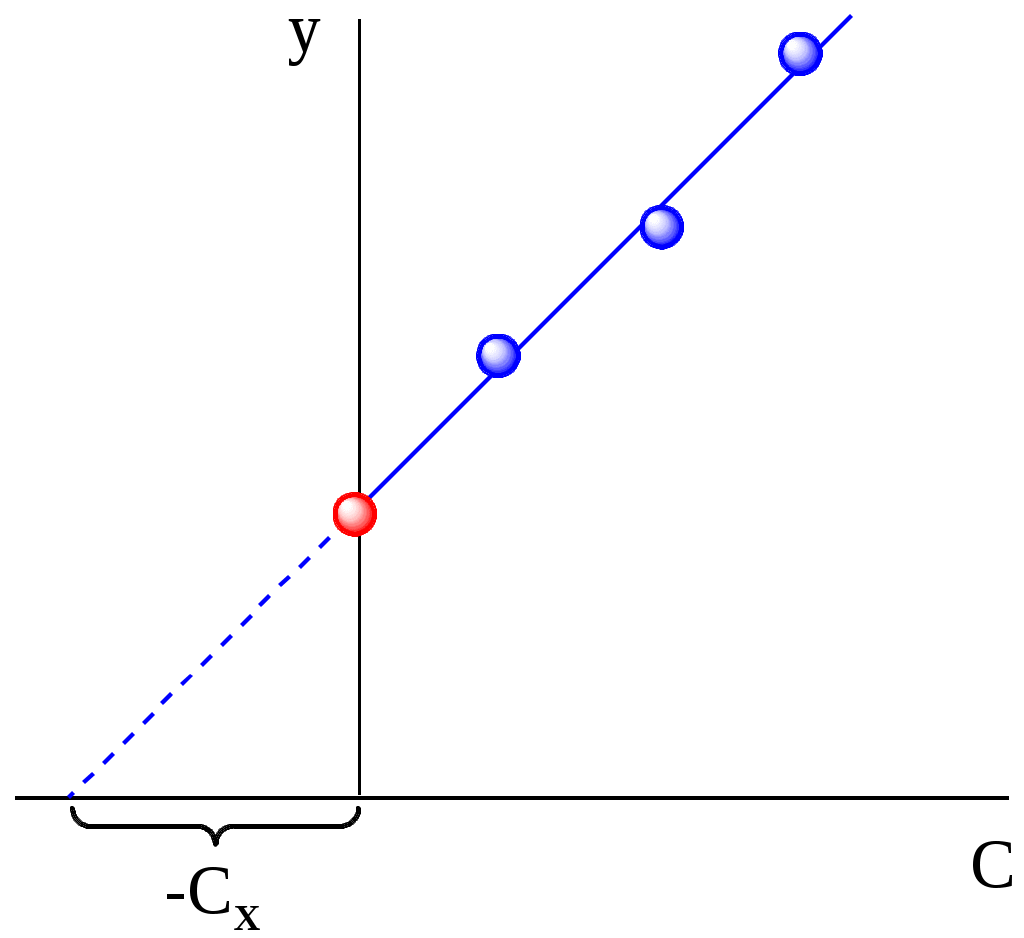

= 0,50 мг/л




Рис. 10.2. Графический метод добавок
В графическом методе добавок берут несколько порций (аликвот) анализируемой пробы, в одну из них добавку не вносят, а в остальные добавляют различные точные количества определяемого компонента. Для каждой аликвоты измеряют величину аналитического сигнала. Затем получают линейную зависимость величины полученного сигнала от концентрации добавки и экстраполируют её до пересечения с осью абсцисс (рис.10.2). Отрезок, отсекаемый данной прямой на оси абсцисс, будет равен неизвестной концентрации определяемого вещества.

10.4. Неопределённость и погрешности измерений

Любой результат анализа всегда имеет некоторую неопределённость. Это связано с особенностью работы приборов, несовершенством работы химика-аналитика при проведении отдельных операций, влиянием посторонних веществ, присутствующих в матрице, реактивах и с другими причинами.

Неопределённость измерения - параметр, связанный с результатом измерения и характеризующий разброс значений (например, ширина доверительного интервала, стандартное отклонение), которые с достаточным основанием могут быть приписаны измеряемой величине.

Погрешность результата - это разность между данным результатом и истинным значением измеряемой величины (абсолютная погрешность ) либо отношение этой разности к истинному значению измеряемой величины (относительная погрешность).

Истинное значение измеряемой величины - идеальная величина, которую можно достичь только в том случае, когда устранены все источники погрешностей измерения и выбрана вся генеральная совокупность.

Неопределённость измерения и погрешность измерения - разные понятия. Погрешность является идеализированным понятием, её нельзя знать точно. Погрешности, как таковой, в каждом опыте соответствует единственное значение, неопределённость выражается в виде интервала. Результат измерения может быть, например, очень близок к истинному значению измеряемой величины, но иметь большую неопределённость.

В зависимости от причины возникновения погрешности бывают



К появлению систематической погрешности могут приводить следующие основные причины:

методические (погрешность отбора пробы, погрешность разделения и концентрирования, пренебрежение сигналом контрольного опыта и т.д.);

реактивные (использование недостаточно чистых реактивов);

инструментальные (использование неправильно градуированного прибора);

индивидуальные (особенности работы химика-аналитика)

Причина грубых погрешностей - неправильная работа химика-аналитика.

10.5. Некоторые основные положения математической статистики, используемые в аналитической химии

Случайной величиной называется измеряемая по ходу опыта численная характеристика, принимающая одно и только одно возможное и наперёд неизвестное значение вследствие действия различных факторов, которые не могут быть заранее учтены.

Дискретной называют случайную величину, множество возможных значений которой конечно либо счётно. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.

Функцией распределения случайной величины называется функция, определяемая равенством

F(x) = P(X  x)

где P(X  x) - вероятность того, что случайная величина X примет любое значение, которое меньше или равно x.

Функция f(x) называется плотностью вероятности непрерывной случайной величины, если для любых чисел a и b (b > a) выполняется равенство

P(a < X < b) =



Явления, носящие случайный характер, также как и закономерные явления подчиняются определённым законам, с помощью которых можно определить, какова будет вероятность того, что случайная величина примет интересующее нас значение. Распределения вероятностей случайных величин могут быть дискретными и непрерывными. Наиболее важным непрерывным распределением вероятностей, используемых в аналитической химии, является нормальное распределение. Примерами одномерного нормального распределения являются идеальный хроматографический пик или полоса поглощения в электронном спектре.

Плотность вероятности нормально распределённой случайной величины описывается формулой: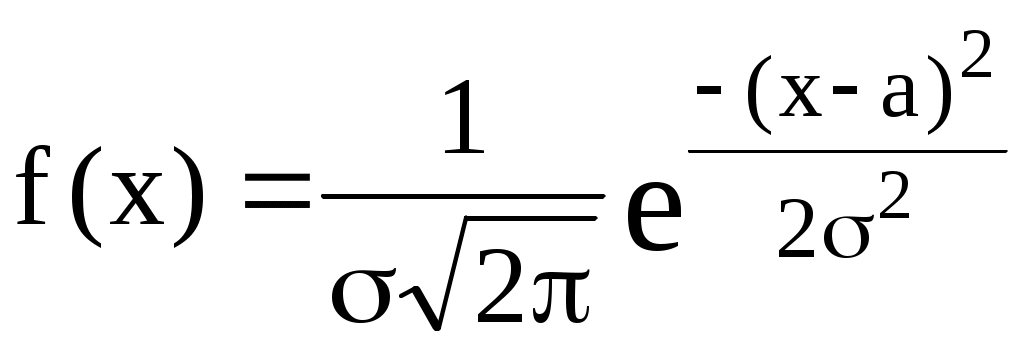



Графики плотности вероятности нормального распределения и функции нормального распределения показаны на рис. 10.3.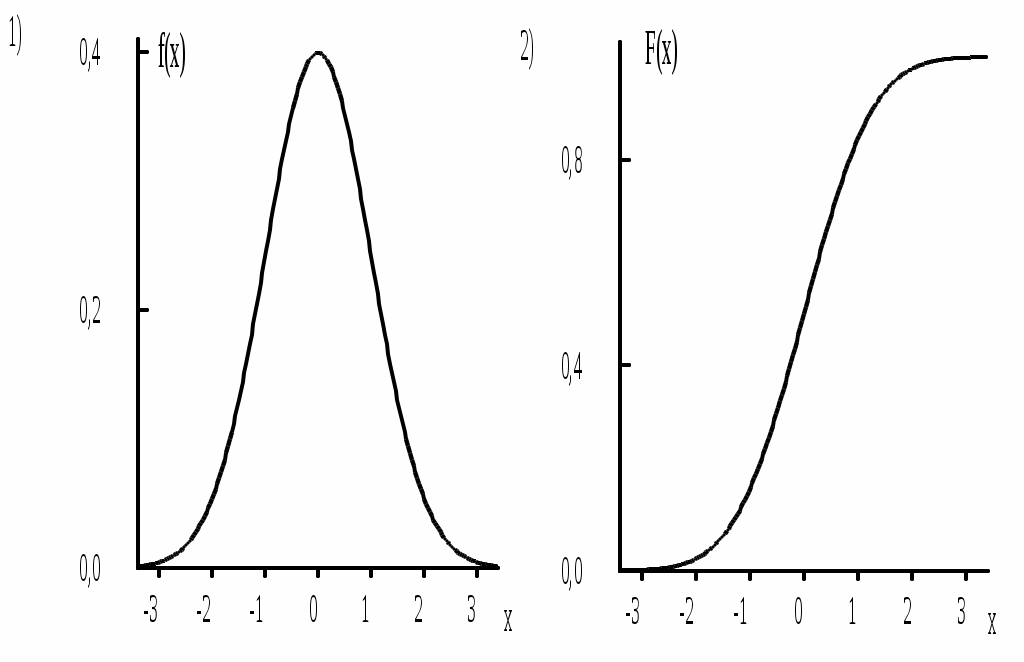



Рис. 10.3. Графики плотности вероятности (1) и функции (2) стандартного нормального распределения(2)

Любое нормальное распределение описывается двумя параметрами: параметр а по смыслу является математическим ожиданием случайной величины и характеризует положение графика функции f(x) относительно числовой оси, параметр  ( > 0), характеризующий растяжение (сжатие) графика, будучи возведённым в квадрат, равен дисперсии случайной величины. Нормальное распределение с а = 0 и  = 1 называется стандартным нормальным распределением.

Вероятность попадания значений нормально распределённой случайной величины в интервал a  3 составляет 99,73%, т.е. практически все значения нормально распределённой случайной величины находятся в этом интервале. Это свойство нормального распределения называется “правилом 3“.

Для характеристики случайной величины на практике пользуются выборкой. Выборкой называется последовательность независимых одинаково распределённых случайных величин. Выборка, пронумерованная в порядке возрастания, т.е. x₁, x₂ ... x_n, называется вариационным рядом. Сами значения x называются вариантами, а n - объёмом выборки. В табл. 10.1 приведены основные характеристики, используемые для описания выборки.

Табл. 10.1.

Основные характеристики, используемые для описания выборки

Характеристика	Определение понятия	Расчётная формула
выборочное среднее	сумма всех значений серии наблюдений, делённая на число наблюдений
выборочная дисперсия (исправленная)	сумма квадратов отклонений, делённая на число степеней свободы. Число степеней свободы f = n-1 - число переменных, которые могут быть присвоены произвольно при характеристике данной выборки
выборочное стандартное отклонение	положительный квадратный корень из выборочной дисперсии
стандартное отклонение выборочного среднего	отношение выборочного стандартного отклонения к положительному квадратному корню из числа наблюдений
относительное стандартное отклонение	отношение выборочного стандартного отклонения к выборочному среднему

Чем меньше число степеней свободы (n-1), тем в большей степени выборочные характеристики отличаются от характеристик случайной величины. Для характеристики выборок малых объёмов (n < 30), взятых из нормально распределённых генеральных совокупностей, используют распределение Стьюдента (t-распределение), представляющее собой распределение случайной величины t

(или )

Данное распределение зависит только от объёма выборки и не зависит от неизвестных параметров a и . При распределение Стьюдента переходит в стандартное нормальное распределение.

Распределение Стьюдента можно использовать для расчёта доверительного интервала выборочного среднего (в том случае, если выборка имеет нормальное распределение). Доверительным интервалом называется интервал, вероятность попадания значений случайной величины в который равна принятой нами доверительной вероятности 1-, где  - уровень значимости (в аналитической практике  = 0,05). Неизвестное математическое ожидание с вероятностью 1- попадёт в интервал:



Например, если  = 0,05 и f = 5, то доверительный интервал для выборочного среднего равен 2,57 .

10.6. Пример статистической обработки результатов измерений. Исключение промахов

Процесс анализа многостадиен. Каждая стадия вносит определённый вклад в неопределённость окончательного результата. Рассмотрим простейший вариант статистической обработки последней стадии анализа - измерения аналитического сигнала.

Пример 10.4. При измерении рН раствора с помощью рН-метра получены следующие результаты 4,32; 4,35; 4,36; 4,98; 4,38; 4,34. Провести статистическую обработку полученных результатов.

Перед началом статистической обработки необходимо проверить, не содержат ли полученные результаты грубых погрешностей. Измерения, в которых обнаружены такие погрешности, должны быть исключены. Их нельзя использовать при дальнейшей статистической обработке результатов. Существует несколько способов исключения грубых погрешностей. Для исключения промахов при работе с выборками малого объёма (n = 4 - 10) можно воспользоваться величиной Q-критерия. Для выборок больших объёмов можно использовать, например, «правило 3» - если значение отличается от среднего более, чем на 3 стандартных отклонения, то его можно считать промахом.

Экспериментальное значение Q-критерия рассчитывают по следующим формулам: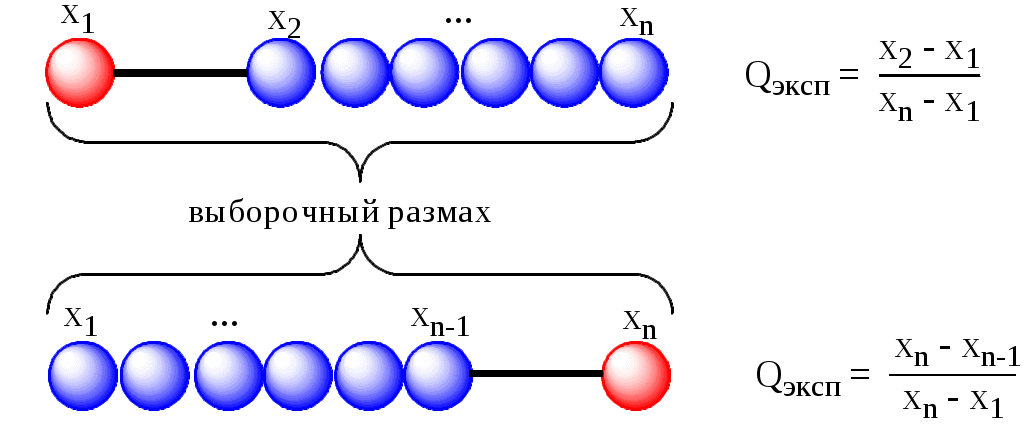



Полученное значение сравнивают с критической (табличной) величиной для Q-критерия. Если оно превышает последнюю, то проверяемый результат является промахом и его необходимо исключить из дальнейших расчётов.

Преобразуем выборку, приведенную в примере 10.4, в вариационный ряд: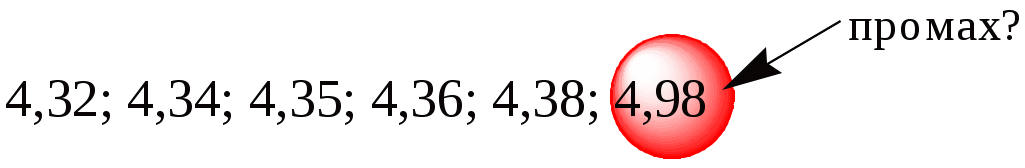



Последнее значение является явно подозрительным. Рассчитаем для него величину Q



Для n= 6 и P = 0,90 Q_крит = 0,48. Следовательно, результат рН = 4,98 является промахом и его необходимо исключить.

При обработке оставшихся данных с помощью формул, представленных в табл. 10.1, получены следующие результаты: = 4,35; = 5,0010^-4; = 2,2410^-2; = 1,0010^-2; = 5,1510^-3; (=0,05) = 0,03. Таким образом, рН = 4,350,03.

Обратите внимание, что окончательный результат среднего значения рН содержит столько же значащих цифр (3), сколько их присутствует в исходных данных. Величина, характеризующая доверительный интервал среднего, имеет столько же десятичных знаков (2), сколько и само среднее. Если бы мы привели в качестве результата, что-нибудь вроде 4,35000,028, то это было бы неверно.

10.7. Основные характеристики методики анализа

Основными характеристиками методики анализа являются воспроизводимость и правильность, предел обнаружения, границы определяемых содержаний и чувствительность.