Редуктора. задача для курс. Проектный и проверочный расчет цилиндрического одноступенчатого прямозубого редуктора
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
Проверка зубьев колеса по контактным напряжениямКонтактная прочность зубьев является основным критерием работоспособности большинства зубчатых передач. При этом рассматривают соприкасание зубьев в полюсе, где происходит однопарное зацепление и возникает выкрашивание. При работе зубчатых передач в результате неточностей изготовления и сборки, деформации зубьев возникают дополнительные динамические нагрузки, влияние которых при расчёте на контактную прочность учитывается коэффициентом 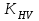 . . Для прямозубой передачи при 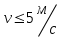 рекомендуется: рекомендуется:- 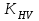 =1,2 – при твёрдости колеса Н≤350НВ, =1,2 – при твёрдости колеса Н≤350НВ,- 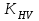 =1,1 – при твёрдости зубьев колеса Н>350НВ. =1,1 – при твёрдости зубьев колеса Н>350НВ.Наибольшее контактное напряжение в зоне зацепления равно: 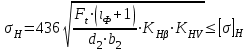 Влияние неравномерного распределения нагрузки по длине зуба при расчёте на контактную прочность зубьев учитывается коэффициентом 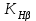 . Для прирабатывающихся колёс . Для прирабатывающихся колёс 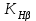 =1,0. =1,0.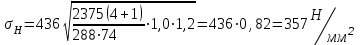 357<375 – контактная прочность зубьев обеспечивается. Проверим нагруженность зубчатой передачи, учитывая расчетные данные через составленную пропорцию: 375 МПа – 100 % 357 МПа – х % 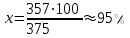 100 % –95%=5% Недогрузка составляет 5%, контактная прочность зубьев обеспечивается. Проверка зубьев колёс по напряжениям изгибаОдним из основных критериев работоспособности зубчатых передач является прочность зубьев на изгиб. При этом зуб рассматривают, как консольную балку, нагруженную сосредоточенной силой Fn, приложенной к зубу в его вершине. Силой трения в зацеплении пренебрегают. Определим коэффициент формы зуба в зависимости от числа зубьев. Коэффициент формы зуба YF Таблица 7
(Пример интерполяции для количества зубьев Z1=27 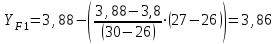 или 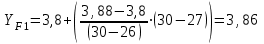 ) )Количество зубьев шестерни совпадает с табличным. Принимаем при Z1=24 YF1=3,92. Количество зубьев колеса Z2=96 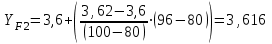 Или 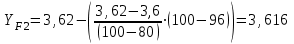 Вся нагрузка зацепления передается одной парой зубьев, которая приложена к вершине зуба и направлена по нормали к его профилю. Фактически зуб представляет собой балку с изменяющейся формой. Это учитывается введением в расчетные формулы теоретических коэффициентов концентрации напряжений, неравномерности распределения нагрузки по ширине зубчатого венца и дополнительной динамической нагрузки в зацеплении. Наибольшее напряжение изгиба равно: 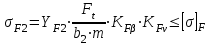 где 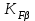 - коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся колёс - коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся колёс 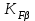 =1,0. =1,0.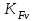 - коэффициент динамической нагрузки. - коэффициент динамической нагрузки.Для прямозубых передач при 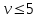 м/с: м/с:- 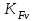 =1,4 при твёрдости зубьев колеса Н≤350НВ, =1,4 при твёрдости зубьев колеса Н≤350НВ,- 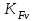 =1,2 при твёрдости зубьев колеса Н>350НВ. =1,2 при твёрдости зубьев колеса Н>350НВ.Тогда напряжения изгиба для колеса равны: 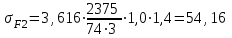 МПа МПа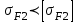 54,16<176МПа, что значительно ниже допускаемых напряжений. Для шестерни: 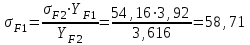 МПа МПа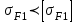 46,95<208МПа, что значительно ниже допускаемых напряжений. Прочность зубьев на изгиб обеспечивается. Произведем окончательную проверку прочности зубьев шестерни и колеса. Для этого необходимо сравнить значения 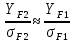 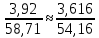 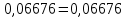 |
