цйу. Документ Microsoft Word (2). Программа дисциплины Статистика
 Скачать 1.87 Mb. Скачать 1.87 Mb.
|
|
Тема 3. Сводка и группировка статистических данных. Ряды распределения Цель изучения темысостоит в формировании системы знаний и компетенций о методах сбора и систематизации статистической информации, в частности о формах и видах статистической сводки и группировки данных, методике построения группировок, построении и графическом представлении рядов распределения. В результате успешного освоения темы Вы: Узнаете: · что такое сводка и группировка данных; · какие виды группировок существуют и для чего они применяются; · как определить, сколько групп можно выделить внутри любой статистической совокупности; · как оформляются результаты группировки данных; · что такое ряд распределения и чем он отличается от группировки; · каким образом можно наглядно представить ряд распределения; · что такое полигон и гистограмма распределения. Приобретете компетенции: · владение методами теоретического и экспериментального исследования; · понимание роли и значения информации в развитии современного общества и экономических знаний; · владение основными методами, способами и средствами получения, хранения, переработки информации; · способность оценивать воздействие макроэкономической среды на функционирование организаций; · способность анализировать финансовую отчетность и принимать обоснованные решения; · владение методами построения и анализа статистических группировок по любому набору первичных статистических данных. В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях: · сводка; · группировка и ее виды; · группировочный признак; · интервал, границы интервала, ширина интервала; · ряд распределения, атрибутивные и вариационные ряды; · частоты, частости; · полигон распределения; · гистограмма распределения; · плотность распределения. Вопросы темы: 1. Статистическая сводка и группировка данных. 2. Ряды распределения. Теоретический материал по теме Вопрос 1. Статистическая сводка и группировка данных. Собранные данные необходимо систематизировать и подготовить к последующей обработке. Для упорядочивания исходных данных статистика применяет два основных метода – метод сводки и метод группировки. Сводка –это научная обработка первичных данных с целью получения обобщенных характеристик изучаемого социально-экономического явления по ряду существенных для него признаков (рис. 11). По глубине и точности обработки данных различают простую и сложную сводку. Данные можно обрабатывать централизовано – в одной организации или децентрализовано – последовательно передавая результаты сводки от территориальных органов в федеральные (как при обработке отчетности). 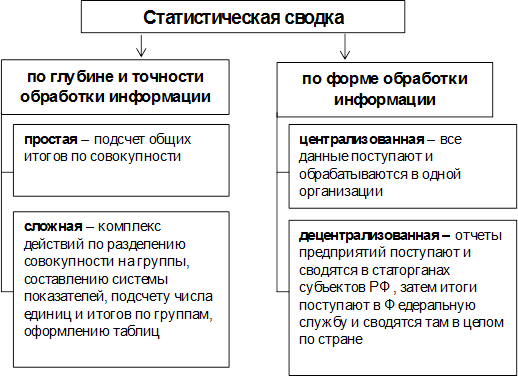 Рис. 11. Виды статистических сводок Группировкой называется разбиение общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на более однородные группы. Группы могут различаться между собой по числу объектов и в качественном отношении. В соответствии с познавательными задачами различают три основных вида группировок (рис. 12).  Рис. 12. Виды группировок Типологическая группировка – это разбиение разнородной совокупности единиц наблюдения на отдельные качественно однородные группы и выявление на их основе устойчивых социально-экономических типов явлений. Например: группировка предприятий и организаций по формам собственности; группировка торговых предприятий по их принадлежности к сферам промышленных и продовольственных товаров. Структурная группировка предназначена для изучения состава совокупности по какому-либо признаку. Например: изучение возрастной структуры безработных в Российской Федерации (табл. 1). Таблица 1. Распределение численности безработных по возрастным группам и средний возраст безработных в 2011 г. (в среднем за год; в процентах к итогу)
Аналитическая группировка выявляет взаимосвязи между изучаемыми признаками. В статистике выделяют факторные и результативные признаки. Факторными называются признаки, под воздействием которых изменяются другие, результативные признаки. Взаимосвязь проявляется в том, что с возрастанием или убыванием значения факторного признака систематически возрастает или убывает значение признака результативного, и наоборот. При построении аналитической группировки, как правило, единицы совокупности группируются по факторному признаку; каждая выделенная группа характеризуется средними величинами результативного признака. Пример аналитической группировки представлен в табл. 2. Таблица 2. Группировка зависимости суммы кредитов, выданных коммерческими банками, от размера процентной ставки
Данные табл. 2 показывают, что с ростом процентной ставки, под которую выдается кредит, средняя сумма кредита, выдаваемая одним банком, уменьшается. Это говорит о том, что между исследуемыми признаками существует обратная связь. По способу построения группировки бывают простые и комбинационные. Простой называется группировка, в которой группы образованы только по одному признаку. Комбинационной называется группировка, в которой образование групп производится по двум и более признакам, взятым в сочетании (комбинации). Рекомендуется сначала группировать единицы по качественным признакам, а затем – по количественным. Например, в группировке водителей автопарка по уровню квалификации (классу) и производительности труда вначале все водители делятся на две группы по классу, а затем внутри каждого класса производится деление по проценту выполнения плана (табл. 3). Таблица 3. Группировка водителей автопарка по классу и производительности труда
Построение статистических группировок включает следующие этапы: 1. Определение группировочного признака. 2. Определение числа групп. 3. Расчет ширины интервала группировки. 4. Выбор признаков, которые будут характеризовать выделенные группы. Группировочным признаком (или основанием группировки)называется количественный или качественный признак, по которому проводится разбиение единиц совокупности на группы. Число выделяемых групп зависит от вида группировочного показателя, степени его вариации и объема изучаемой совокупности. Если группировочный признак качественный, то число групп будет равно числу вариантов этого признака. Например, группируя сотрудников по полу, мы получим 2 группы: сотрудники-мужчины и сотрудники-женщины. При определении числа групп необходимо учесть размахвариации группировочного признака (R), который определяется по формуле: R = Хmax – Хmin, (1) где Хmax – максимальное значение группировочного признака; Хmin – минимальное значение группировочного признака. Чем больше размах вариации группировочного признака, тем большее число групп может быть образовано. Однако при слишком большом их числе возникает проблема «пустых» групп, т.е. не содержащих ни одного объекта. Число групп можно определить математически или экспертным путем. Математический способ предполагает использование формулы Стерджесса, которая дает хорошие результаты при большом объеме совокупности: m = 1 + 3,322 ´ lg n, (2) где m – число выделяемых групп; n – общее число единиц совокупности. Полученное в результате расчетов значение округляют до целого числа по стандартным правилам округления. Интервал – это значения признака, лежащие в определенных границах. Нижней границей называется наименьшее, а верхней границей – наибольшее значение признака в интервале. Ширина интервала – это разность между его верхней и нижней границами. По ширине интервалы группировки бывают равные (одинаковые) (табл. 4) и неравные (табл. 5). Таблица 4. Группы коммерческих банков по величине балансовой прибыли
Ширина каждого интервала составляет 200 млн руб: 400 – 200 = 600 – 400 = 800 – 600 = 200 Таблица 5. Группы фирм по объему инвестиций
Ширина интервалов неодинакова: · 20 – 10 = 10 млн руб. · 40 – 20 = 20 млн руб. · 80 – 40 = 40 млн руб. Ширина равного интервала h определяется по следующейформуле: где хmax, xmin – максимальное и минимальное значения признака в совокупности; m – число выделяемых в совокупности групп. Существуют следующие правила округления ширины интервала h: · Если h имеет один знак до запятой (например: 0,67; 1,487; 3,82), полученные значения округляют до десятых (0,7; 1,5; 3,8.). · Если h имеет две значащие цифры до запятой (например, 14,876), это значение округляют до целого числа (15). · В случае, когда h является трех-, четырех- или еще более значимым числом, его величину следует округлить до ближайшего числа, кратного 100 или 50. Например, 652 следует округлить до 650 или до 700. Интервалы группировки бывают также закрытыми(табл. 6.) и открытыми (табл. 7.). Таблица 6. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
