расчет длины общей нормали. Расчет длины общей нормали Длина общей нормали
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
= 69,364 мм; 5) по табл. 2.8 найдем Е1 =0,100 мм; 6) по табл. 2.9 определим допуск радиального биения Fr =71мкм; 7) по табл. 2.8 найдем Е2= 0,018 мм при Fr= 71мкм; 9) по ф.(3) рассчитаем действительную длину общей нормали 10) по табл. 2.10 определим допуск на среднюю длину общей нормали ТWm= 0,090 мм. Таким образом, во вторую часть таблицы параметров на чертеже цилиндрического прямозубого колеса запишем: «Длина общей нормали W = 69,25 –0,09». Для косозубых и шевронных колес при вычислении длины общей нормали по ф. (2) и ф. (3) используют те же таблицы, что и для прямозубых колес, но расчет проводят для условного числа зубьев ZУ и вводят поправку длины общей нормалиWУ. Условное число зубьев вычисляют по зависимости: ZУ = Z . k. Коэффициент“k” зависит от угла наклона зубьев (табл. 2.11). Как правило, условное число зубьев получается не целым, поэтому в расчет вводят поправку: WУ =0,0149 . (ZУ – Z * ),(4) где Z *– целая часть условного числа зубьев. Таблица 2.11 – Значения коэффициента “k” [3, c.134]
В остальном, расчет длины общей нормали и допуска на её величину для косозубых и шевронных колес не отличается от расчета для прямозубых колес. пример № 2. Вычисление длины общей нормали для косозубого цилиндрического колеса: Z = 42, m = 5 мм, x= 0, β = 14 о 22 ’ , внешнее зацепление, степень точности 8 – С. 1. вычислим делительный диаметр колеса: d = m . Z / cos 14 o 22 ’ = 216,78мм; 2. по табл. 2.11 определим k = 1,0948 и ZУ = k . Z = 1,0948 . 42=45,98; 3. по табл. 2.6 определим охватываемое число зубьев ZW = 6 и W ’ =16,8670 мм; 4. вычислим поправку WУ = 0,0149 . (ZУ –Z * )= 0,0149 . (45,98 – 45) = 0,0146 мм; 5. по ф.(2) рассчитаем номинальную длину общей нормали: W * = (W ’ + Wу + 0.684x) m =(16,8670 + 0,0146 + 0) . 5 = 84,408мм; 6. по табл. 2.7 найдем Е1= 0,100 мм; 7. по табл. 2.9 определим допуск радиального биения Fr = 71 мкм; 8. по табл. 2.8 найдем Е2= 0,018 мм при Fr = 71 мкм; 9. вычислим наименьшее отклонение средней длины общей нормали: ЕWms = Е 1+ Е2 = 0,100+0,018 = 0,118 мм; 10. по ф.(3) рассчитаем действительную длину общей нормали W = (W * – ЕW ms ) =(84,408 – 0,118 ) = 84,39 мм. 11. по табл. 2.10 определим допуск на среднюю длину общей нормали ТWm = 0,090 мм. Таким образом, во вторую часть таблицы параметров на чертеже цилиндрического косозубого (или шевронного) колеса запишем: «Длина общей нормали W = 84,39 –0,09». Дата добавления: 2015-07-13 ; Просмотров: 11697 ; Нарушение авторских прав? ; Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет Зубчатые передачи находят широкое применение в различных видах машин и механизмов, исполняя роль передаточного механизма. Они определяют качество, надежность, работоспособность и долговечность машин, станков, приборов и других изделий. Расчет геометрических параметров зубчатых передач необходим с конструкторской точки зрения, так как определяет основные размеры и габариты передачи, а также с технологических позиций, так как влияет на выбор оборудования и методов обработки. Наиболее широко применяются эвольвентные цилиндрические зубчатые передачи внешнего и внутреннего зацепления с исходным контуром, профилирующим режущий инструмент по ГОСТ 13755. Исходный контур выполняется в виде прямозубой рейки с углом α = 20°. Прямозубые колеса имеют направление зуба вдоль оси колеса. У косозубых колес зуб направлен под утлом βк оси колеса. Основным геометрическим параметром, определяющим все элементы передачи, является модуль — т, который выбирается в зависимости от передаваемой нагрузки из нормального ряда модулей по ГОСТ 9563 . Модуль – это число, показывающее, сколько миллиметров диаметра делительной окружности приходится на один зуб зубчатого колеса. Зубчатые колеса с модулем от 0,05 мм до 1 мм принято называть мелкомодульными; от 1 до 10 мм – среднемодульными и свыше 10 мм – крупномодульными. Основное применение находит первый ряд модулей: 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16. Второй ряд применяется ограниченно: 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5; 7; 9; 11; 14; 18. Мелкомодульные передачи (m — длина общей нормали W или средняя длина общей нормали Wm. Длина общей нормали – это расстояние между двумя параллельными плоскостями, касательными к двум разноименным, активным боковым поверхностям зубьев колеса. Номинальное значение длины общей нормали определяется по формуле: где Zw = 0,111 z + 0,5 или Zw = z/9 + 1 – число охватываемых при измерении зубьев, которое необходимо округлять до ближайшего целого числа (таблица 7.1). Для колес с углом зацепления α = 20° формула принимает вид: Длина общей нормали прямо пропорциональна модулю, поэтому в таблицах справочников указывается значение длины общей нормали для т = 1 (см. таблицу 7.1). При изменении модуля табличное значение необходимо умножить на величину модуля. Средняя длина общей нормали определяется по результатам измерения всех длин у колеса от зуба к зубу, как среднее арифметическое значение: Wm = Ввиду погрешностей обработки, у одного зубчатого колеса длина общей нормали изменяется от зуба к зубу. Для размещения смазки и исключения заклинивания требуется увеличивать или уменьшать толщину зуба. Теоретическое зацепление считается двухпрофильным, когда контакт идет по обеим сторонам зуба. Реальная передача имеет однопрофильное зацепление, т.е. по рабочим профилям – контакт, а по нерабочим – зазор. Таблица 7.1 – Геометрические параметры зубчатого колеса при m = 1, α = 20 °С
Величина бокового зазора зависит от условий эксплуатации: температуры, смазки, нагрузки, условий загрязнения и других требований (см. п. 7.3). У зубчатого колеса различают окружной шаг по делительной окружности: и шаг зацепления или основной шаг (шаг по основной окружности): Pb = Pt cos α = π т cos α. 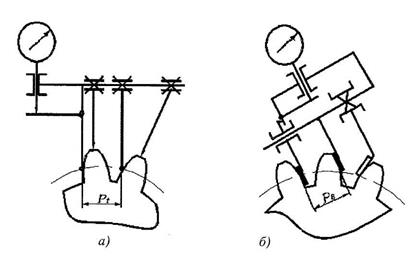 Рисунок 7.1 – Схема измерения шаговых параметров зубчатого колеса: а – окружного шага; б – шага зацепления Контроль окружного шага может быть выполнен накладным шагомером или универсальным зубоизмерительным прибором. Базирующие наконечники опираются на наружный (или внутренний) диаметр (рисунок 7.1, а). Широко используется метод измерения от «первого шага», принятого за номинальное значение с определением отклонений от него. Измерив по всей окружности Z раз, можно построить график и определить накопленную погрешность окружного шага. Шаг зацепления (основной шаг) контролируется в плоскости, касательной к основному цилиндру (рисунок 7.1, б). Настройка прибора производиться на ноль по блоку кольцевых мер длины, равному номинальному значению шага зацепления. Метод измерения относительный, так как прибор показывает погрешность шага зацепления: Дата добавления: 2015-05-08 ; просмотров: 2146 | Нарушение авторских прав Касательную к основной окружности зубчатого колеса, которая пересекает zw зубьев его и является нормалью к обеим крайним эвольвентам, называют общей нормалью. Расстояние между разноименными боковыми поверхностями зубьев цилиндрического колеса по общей нормали к этим поверхностям называют длиной общей нормали W (рис. 2). Длина общей нормали не зависит от того, в каких точках профилей зубьев эта нормаль пересекает две встречные эвольвенты. Изменение длины общей нормали пропорционально изменению смещения исходного контура xm зуборезного инструмента. Важно также, что контроль размера w не связан с какой-либо вспомогательной базой для установки мерительного инструмента. Указанные свойства общей нормали показывают преимущество данного способа контроля толщины зуба колеса. Этот размер можно измерять штангенциркулем, микрометром, специальной предельной скобой. 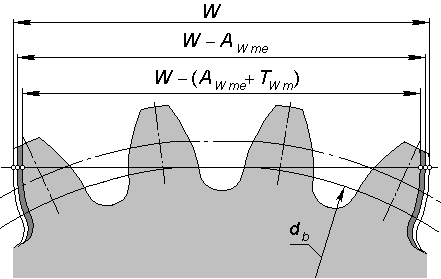 Длину общей нормали для цилиндрических колес с внешними прямыми зубьями рассчитывают по следующей формуле [ 2 ] 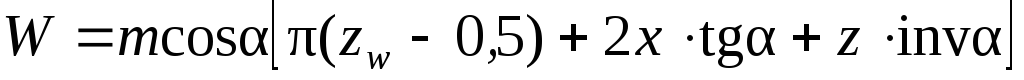 , ,где m – модуль, мм; a – угол профиля исходного контура, по стандарту ГОСТ 13755-81 a =20 0 ; zw – число зубьев в длине общей нормали; x – коэффициент смещения; z – число зубьев контролируемого колеса; inv a – эвольвентный угол, соответствующий углу профиля a, для прямозубых колес inv a = tg a — a. Длину общей нормали для цилиндрических колес с внешними косыми зубьями рассчитывают по аналогичной формуле 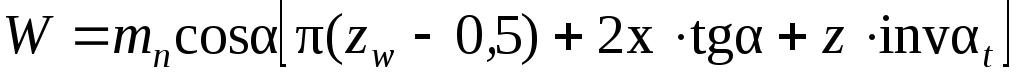 , ,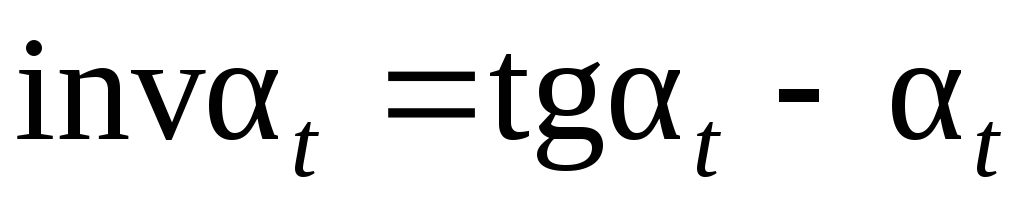 , а торцовый угол профиля исходного контура , а торцовый угол профиля исходного контура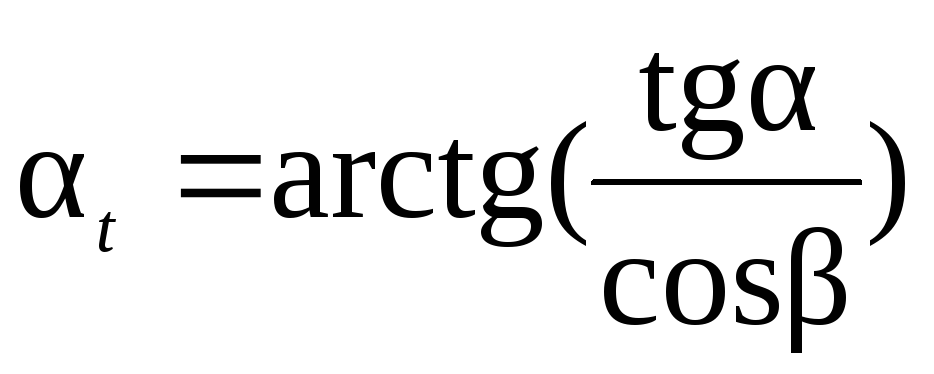 . Здесь – задаваемый чертежом зубчатого колеса делительный угол наклона линии зуба. . Здесь – задаваемый чертежом зубчатого колеса делительный угол наклона линии зуба.Для косозубого колеса длину общей нормали измеряют под основным углом наклона линии зуба b к торцу колеса, а возможность замера проверяют при достаточной ширине зубчатого венца b по условию Число зубьев в длине общей нормали zw для цилиндрических колес с прямыми зубьями должно удовлетворять условию 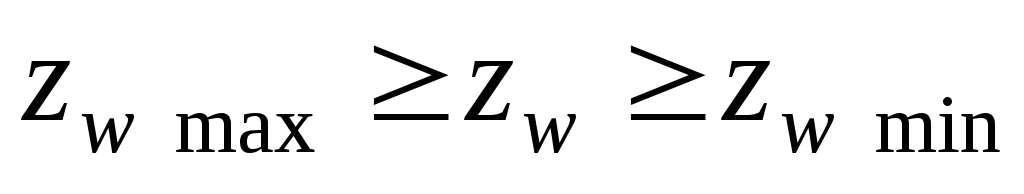 , ,когда 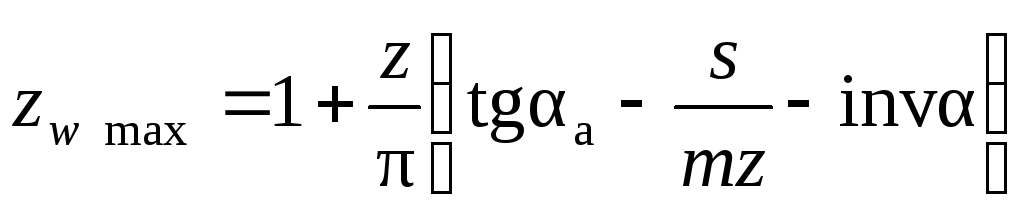 , ,  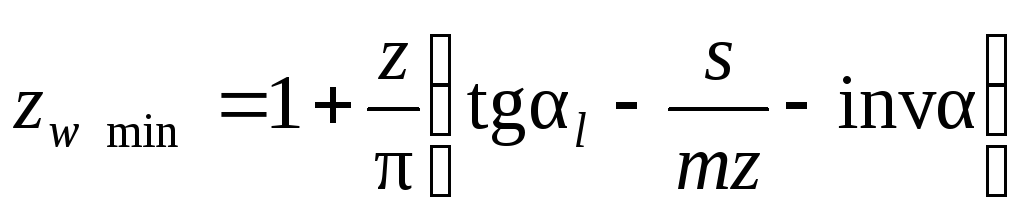 , ,Здесь a — угол профиля в точке на окружности вершин зубьев; l — угол профиля в граничной точке. При небольших коэффициентах смещения (x 1) для определения zw можно пользоваться упрощенной формулой 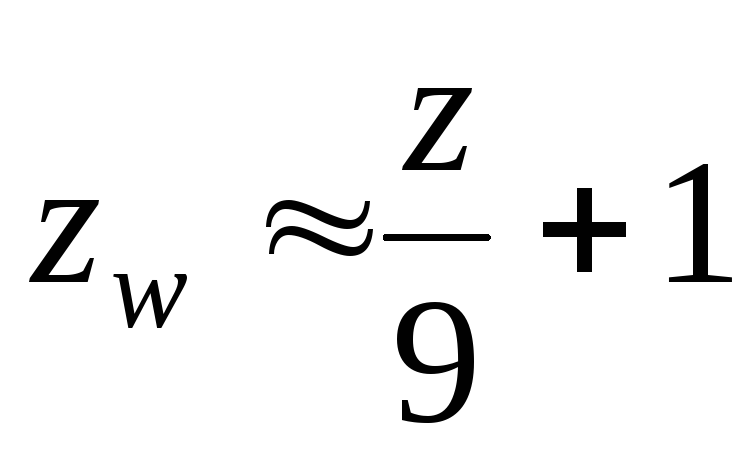 с округлением полученного значения до ближайшего целого значения. 1.3. Допуски на измерительные размеры цилиндрических зубчатых колес Рассмотренные выше формулы для вычисления номинальных измерительных размеров цилиндрических зубчатых колес гарантируют беззазорное зацепление колес в передаче. В реальных зубчатых передачах должен быть обеспечен гарантированный боковой зазор с целью устранения заклинивания зубьев при работе под нагрузкой в результате температурных деформаций деталей передачи, а также для размещения слоя смазки на рабочих профилях зубьев. Боковой зазор в зацеплении необходим также для компенсации погрешностей изготовления и монтажа передачи. Он определяется в основном величиной межосевого расстояния aw передачи и толщиной s зубьев колес. Стандартом на эвольвентные зубчатые цилиндрические передачи (ГОСТ 1643-81) установлено восемь видов допусков на боковой зазор: h, d, c, b, a, z, y, x (обозначения допусков расположены в порядке возрастания величины допуска). Принятая величина гарантированного бокового зазора является основой для назначения вида сопряжения зубчатых колес. Этим же стандартом предусмотрено шесть видов сопряжения: H – нулевой зазор, E – малый зазор, C и D – уменьшенный зазор, B – нормальный зазор, A – увеличенный зазор. Сопряжения видов Н, Е и С требуют повышенной точности изготовления зубьев колес. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности передачи, а также при наличии крутильных колебаний валов передачи. Чаще всего в среднем машиностроении используют передачи с видами сопряжения В и С. При отсутствии специальных требований к зубчатой передаче с каждым видом сопряжения употребляется определенный вид допуска на боковой зазор, обозначаемый строчной буквой, аналогичной букве вида сопряжения (например, А — а, В — в, С — с и т. д.). Поле допуска на измерительный размер зубчатого колеса всегда направлено в тело зуба, поэтому предельные отклонения измерительного размера (верхнее и нижнее) всегда имеют отрицательные значения [ 1 ].  Таблица 1
Таблица 2
Таблица 3
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
