Расшифровка маркировки, область применения (агрессивное воздействие среды, давление, температура)
 Скачать 7.79 Mb. Скачать 7.79 Mb.
|
|
41. Основы массопередачи. Классификация процессов массообмена. Массообмен, массоотдача, массопередача. Диффузионный и конвективный механизмы массообмена. Равновесие и движущая сила массопередачи. Технологические процессы, скорость протекания которых определяется скоростью переноса вещества из одной фазы в другую, называются массообменными, а аппараты, в которых происходят эти процессы, – массообменными аппаратами. В разделительном аппарате могут производиться разнообразные процессы. Основными и важнейшими из них являются абсорбция, ректификация, экстракция, кристаллизация, адсорбция, сушка, ионнообменные процессы и мембранное разделение. Абсорбцией называется процесс разделения, основанный на избирательном поглощении газов или паров жидкими поглотителями – адсорбентами. В процессе абсорбции имеет место переход вещества или группы веществ из газовой (паровой) фазы в жидкую. Обратный процесс называется десорбцией. Ректификацией называется процесс разделения смеси жидкостей, имеющих различные температуры кипения при соответствующем давлении, на чистые или обогащенные составляющие в результате противоточного движения потоков пара и жидкости. В процессе ректификации имеет место переход вещества или группы веществ из жидкой фазы в паровую, и наоборот. Экстракцией называется процесс разделения, основанный на извлечении растворенного в одной жидкости вещества или группы веществ другой жидкостью, которая не смешивается или только частично смешивается с первой. Процесс применяется в тех случаях, когда из раствора необходимо извлечь растворенное вещество или группу веществ. В этом процессе имеет место переход вещества из одной жидкой фазы в другую жидкую фазу. Адсорбцией называется процесс разделения, основанный на избирательном поглощении газов, паров или растворенных в жидкостях веществ, твердым пористым поглотителем – адсорбентом, способным поглощать одно или несколько веществ из их смеси. В этом процессе вещества переходят из газовой или жидкой фаз в твердую. Обратный процесс называется десорбцией. Ионнообменный процесс представляет собой процесс извлечения вещества из раствора, основанный на способности некоторых твердых веществ (ионитов) обменивать свои подвижные ионы на ионы извлекаемого вещества. Процесс применяется для извлечения веществ из растворов, имеющих низкую концентрацию.В этом процессе вещества переходят из жидкой фазы в твердую. Сушкой называется процесс удаления влаги из твердых влажных материалов путем ее испарения. В этом процессе имеет место переход влаги из твердого влажного материала в паровую или газовую фазу. Кристаллизацией называется процесс разделения, основанный на выделении вещества в виде твердой фазы (кристаллов) из жидкой фазы. Процесс имеет место в тех случаях, где требуется получение веществ повышенной чистоты. В этом процессе происходит переход вещества из жидкой фазы в твердую фазу. Обратный процесс – растворение. Мембранное разделение основано на способности определенных тонких пленок (полупроницаемых мембран) пропускать одни вещества и задерживать другие. В этом процессе вещества переходят через полупроницаемую мембрану из исходной жидкости или газа в жидкую или газовую фазу, находящуюся за мембраной. Из краткой характеристики следует, что для всех массообменных процессов характерным является переход вещества из одной фазы в другую, или массопередача. Одну фазу обозначим буквой G, другую L, а распределяемый компонент М. Поскольку все массообменные процессы обратимы, то распределяемое вещество может переходить в зависимости от концентрации этого вещества в распределяющих фазах из фазы Gв фазуLи наоборот. Представим для первой группы процессов массопередачи, что распределяемое вещество находится вначале только в фазе G и имеет концентрацию  . В фазе L в начальный момент распределяемого вещества нет и, следовательно, концентрация его в этой фазе . В фазе L в начальный момент распределяемого вещества нет и, следовательно, концентрация его в этой фазе  =0. =0.Если распределяющие фазы привести в соприкосновение, начнется переход распределяемого вещества из фазы Gв фазу L, и в жидкой фазе появится распределяемый компонент с концентрацией, отличной от нуля. С момента появления вещества М в фазе Lначинается обратный переход его в фазу G. До некоторого момента времени число частиц М, переходящих в единицу времени через единицу поверхности фазового контакта из фазы G в фазу L, больше, чем число частиц, переходящих обратно из фазы L в фазу G. Через определенный промежуток времени скорости перехода распределяемого вещества из фазы G в фазу L и обратно становятся одинаковыми. Такое состояние называется равновесным. В состоянии равновесия существует строго определенная зависимость между концентрациями распределяемого вещества в фазах, которые при равновесии системы называются равновесными. Любой концентрации  соответствует равновесная концентрация соответствует равновесная концентрация  , и наоборот, любой концентрации , и наоборот, любой концентрации  соответствует равновесная концентрация соответствует равновесная концентрация 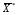 , т. е. имеют место зависимости вида , т. е. имеют место зависимости вида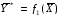 или или  . .Условия равновесия и равновесные зависимости могут быть выражены не только через концентрации, но и через другие параметры, например, энтальпии, химический потенциал. Движущей силой массопередачи является разность между рабочей и равновесной концентрациями или наоборот. Движущую силу можно выражать либо через концентрации распределяемого вещества в фазе G, либо L. В этой связи уравнения массопередачи, записанные по фазам, имеют вид  , , . (1.7) . (1.7)Индексы у коэффициента скорости процесса 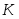 показывают, какие концентрации приняты для выражения движущей силы. В общем случае показывают, какие концентрации приняты для выражения движущей силы. В общем случае  и и    , но всегда выполняется равенство , но всегда выполняется равенство . (1.8) . (1.8)42. Уравнение массоотдачи, коэффициент массоотдачи. Уравнение массопередачи, коэффициент массопередачи. Материальный баланс массопередачи. Уравнение рабочей линии.      43 Средняя движущая сила массопередачи. Расчет средней движущей силы массопередачи. Число единиц переноса. Высота единицы переноса. Дифференциальное уравнение конвективной диффузии. Движущей силой массообменных процессов является разность между рабочей и равновесной концентрациями или наоборот. Это зависит от того, которая из указанных концентраций больше. Движущую силу можно выражать либо через концентрации распределяемого вещества в фазе G, либо L. В этой связи уравнения массопередачи, записанные по фазам, имеют вид  , , . (1.7) . (1.7)Индексы у коэффициента скорости процесса  показывают, какие концентрации приняты для выражения движущей силы. В общем случае показывают, какие концентрации приняты для выражения движущей силы. В общем случае  и и    , но всегда выполняется равенство , но всегда выполняется равенство . (1.8) . (1.8)В этой связи для всего процесса массообмена, протекающего в пределах изменения концентраций от начальных до конечных, должна быть определена средняя движущая сила по газовой фазе  или жидкой – или жидкой – 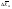 . .С учетом средней движущей силы процесса основное уравнение массопередачи для всей поверхности контакта фаз может быть записано в виде  , (1.9) , (1.9) . (1.10) . (1.10)При определении движущей силы возможны два случая: – зависимость между равновесными концентрациями не линейна и определяется функциональной зависимостью самого общего вида типа 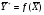 ; ;– зависимость между равновесными концентрациями линейная – (  – представляет собой постоянную величину). – представляет собой постоянную величину).Определим среднюю движущую силу по фазе G для случая перехода распределяемого компонента из газовой в жидкую фазу. Для элемента поверхности имеем  ; ;  . . Из сопоставления предыдущих равенств получим 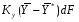 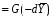 для элементарной поверхности фазового контакта имеем 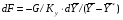 . .После интегрирования в пределах 0 –F и 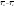 получим получим . (1.11) . (1.11)Изменим границы интегрирования с целью исключения отрицательного знака перед интегралом и вставим равенство для  : : . (1.12) . (1.12)При выражении движущей силы для жидкой фазы получим аналогичное выражение: 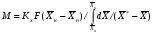 . (1.13) . (1.13)При сравнении уравнений (1.9) и (1.10) с уравнениями (1.12) и (1.13) составим выражения для средних движущих сил по газовой и жидкой фазам:  , (1.14) , (1.14) . (1.15) . (1.15)Интегралы, стоящие в правой части равенств (1.14) и (1.15), называют числами единиц переноса – сокращенно ЧЕП. Отсюда выражение для ЧЕП в газовой фазе имеет  , ,а выражение для ЧЕП в жидкой фазе:  . .Число единиц переноса, как следует из уравнений (1.14) и (1.15), можно определять по средней движущей силе процесса:  , , . .Физический смысл ЧЕП состоит в том, что эта величина характеризует изменение рабочей концентрации фазы, приходящееся на единицу движущей силы. Числа единиц переноса выражаются интегралами, которые не могут быть решены аналитически, так как вид функции  или или 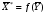 в каждом конкретном случае различен. В связи с этим число единиц переноса в каждом конкретном случае различен. В связи с этим число единиц переноса  и и  определяют методом графического или численного интегрирования. определяют методом графического или численного интегрирования.При графическом интегрировании (рис. 1.5) задаются рядом значений  , промежуточных между величинами , промежуточных между величинами  и и  . .  Рис. 1.5. К расчету числа единиц переноса методом графического интегрирования Строят кривую зависимости 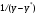 от от  . Измеряют площадь, ограниченную крайними ординатами, соответствующими . Измеряют площадь, ограниченную крайними ординатами, соответствующими  и и 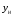 , и осью абсцисс (площадь , и осью абсцисс (площадь  , заштрихованная на рисунке). После этого находят величину искомого интеграла с учетом масштабов , заштрихованная на рисунке). После этого находят величину искомого интеграла с учетом масштабов  и и  осей ординат и абсцисс: осей ординат и абсцисс:  Аналогично, пользуясь графиком зависимости 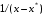 от от  , определяют величину , определяют величину  . .Достаточно часто за основную характеристику аппарата принимают его высоту. Обозначим площадь поперечного сечения и высоту аппарата, соответственно f и H, тогда  . Из уравнения (1.11) после изменения пределов интегрирования и решения относительно высоты аппарата для газовой фазы получим . Из уравнения (1.11) после изменения пределов интегрирования и решения относительно высоты аппарата для газовой фазы получим . .Комплекс  имеет размерность длины [м] и физический смысл, состоящий в том, что он представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП). Обозначим имеет размерность длины [м] и физический смысл, состоящий в том, что он представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП). Обозначим  , , . .Тогда уравнения массопередачи по фазам можно записать следующим образом:  , , . .Высота, эквивалентная единице переноса, по смыслу соответствует величине, обратной объемному коэффициенту массопередачи, а число единиц переноса – величине, обратной движущей силе процесса. Чем выше интенсивность массопередачи в аппарате, тем меньше в нем величина ВЕП. Значения ВЕП определяются по эмпирическим формулам для различных типов аппаратов. Отметим также, что ВЕП используется только для расчета аппаратов с постоянным поперечным сечением рабочей части. Дифференциальное уравнение массоотдачи (конвективной диффузии). Согласно теории диффузионного пограничного слоя распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией. Рассматриваемая система состоит из двух частей: ядра и пограничного диффузионного слоя, включающего в себя достаточно тонкий ламинарный подслой. В ядре перенос вещества осуществляется преимущественно токами жидкости в условиях достаточной турбулентности. Концентрация распределяемого компонента в ядре турбулизированного потока фазы принимается постоянной (  .) .)По мере приближения к пограничному диффузионному слою турбулентный перенос затухает и с приближением к границе раздела фаз в ламинарном подслое начинает превалировать перенос за счет молекулярной диффузии. Соответственно этому появляется градиент концентрации распределяемого компонента, увеличивающийся по мере приближения к границе. При конвективной диффузии бесконечно малый элемент потока перемещается из одной точки пространства в другую. В этом случае изменение концентрации распределяемого компонента может быть выражено субстанциональной производной, которая учитывает изменение ее во времени и изменения, связанные с перемещением элемента из одной точки пространства в другую  . (1.21) . (1.21)В этом равенстве  представляет собой локальное изменение концентрации распределяемого компонента, а комплекс представляет собой локальное изменение концентрации распределяемого компонента, а комплекс  – конвективное изменение концентрации. – конвективное изменение концентрации.Если в уравнении молекулярной диффузии    . (1.17) заменить локальное изменение концентрации . (1.17) заменить локальное изменение концентрации  полным полным 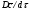 , то можно получить дифференциальное уравнение конвективной диффузии: , то можно получить дифференциальное уравнение конвективной диффузии: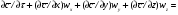  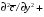  (1.22) (1.22)44 Основы технологического проектирования массообменных аппаратов. Расчет диаметра массообменных аппаратов. Расчет диаметра противоточных колонн. Гидродинамические режимы течения жидкости в противоточных насадочных и тарельчатых колоннах. Явление уноса.   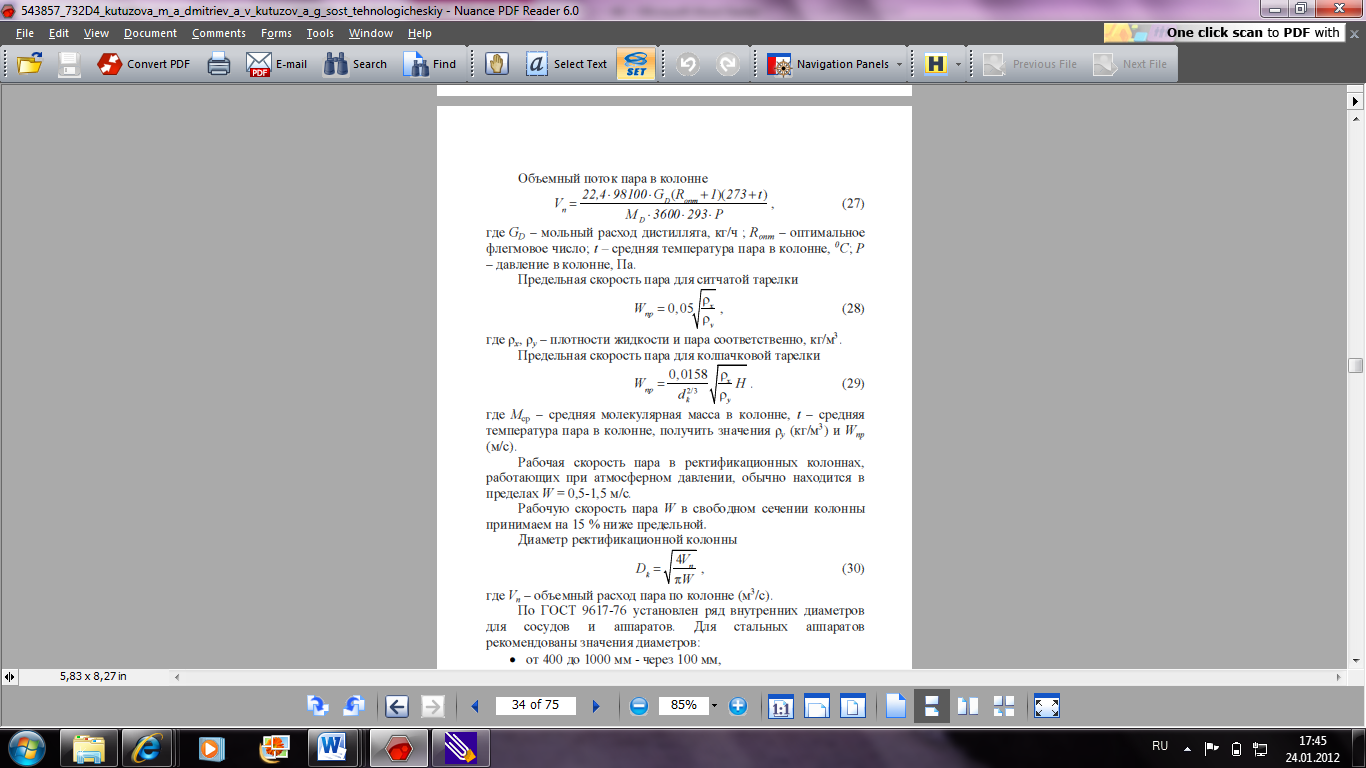  |
