Расшифровка маркировки, область применения (агрессивное воздействие среды, давление, температура)
 Скачать 7.79 Mb. Скачать 7.79 Mb.
|
|
8. Сосуды высокого давления (толстостенные). Причины разделения сосудов на тонко и толстостенные. Напряжения, возникающие в толстостенной цилиндрической оболочке под действием внутреннего избыточного давления, построение эпюр напряжений. Анализ формул и эпюр. К аппаратам высокого давления (толстостенные) относят аппараты, работающие под давлением свыше 10 МПа. Толщина стенки корпуса такого аппарата превышает 10% его внутреннего диаметра, т.е. коэффициент толстостенности (отношение наружного диаметра к внутреннему) β = Dн/D>1,2. Обычно аппараты высокого давления изготавливают по возможности меньшего диаметра, что позволяет получить относительно небольшое усилие от внутреннего давления на крышку аппарата и тем самым обеспечить конструктивное совершенство ее элементов уплотнения. Наиболее употребительные отношения диаметра корпуса к его высоте D/H: 1:10 и 1:15. Толщина стенки толстостенных сосудов может достигать 600 мм при D = 1м. Корпуса аппаратов в зависимости от способа их изготовления бывают литые, кованые, сварные и многослойные. Для толстостенных оболочек нельзя применять распределение σt по толщине стенки равномерным и пренебрегать радиальным напряжением, т.к. давление может достигать порядка 600 МПа и тогда σr = 600 МПа (на внутренних волокнах), что значительно больше допускаемых напряжений и соизмеримо с σt. В этом случ. напряж. сост. материала оболочек – объёмное (трехосное). Основные причины, по которым аппараты подраздел.на тонко- и толстостенные:
– для тонкостенных – двухосное (σr ≈0; σm≠0; σt≠0 ); – для толстостенных – объёмное (σr ≠0; σm≠0; σt≠0); 2. различный характер распределения тангенциальных напряжений но толщине стенки: - для тонкостенных - равномерное; - для толстостенных - неравномерное. Основными признаками деления сосудов на тонко- и толстостенные являются соотношение толщины стенки S к внутреннему диаметру Dв значение давлений, Т.е. - для тонкостенных а) S-C/ Dв ≤0,1 (при Dв> 200 мм) или β = Dн/ Dв<1,2, где β - коэф. толстостенности; б) Р≤10 МПа (условное разделение)  - для толстостенных а) S-C/ Dв>0,1; β>1,2; б) Р>10 МПа Цель расчета толстостенных аппаратов заключается в получении формул для нахождения напряжений σr; σm; σt. В цил.обечайке без днищ возникают радиаль. и тангенц. Напряжения: 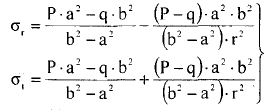 Здесь r – текущий радиус, т.е. значение, при котором необходимо рассчитать напряжение. Величина r может выбираться в пределах от r = a до r = b. Если цилиндрическая обечайка имеет днища, то при действии на них внутреннего и наружного давлений возникает меридиональная сила U и соответственно меридиональное напряжение σm. 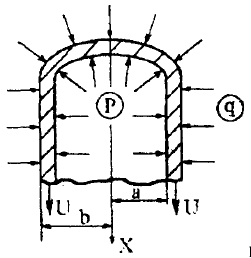 Обычно q = 0, тогда уравнения упрощаются: 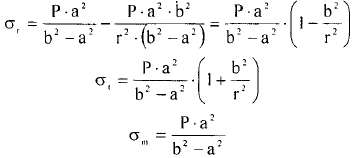 Сравнивая σm с суммой напряжений (σt+ σr), получим зависимость, связывающую все 3 напряжения между собой, т.е. Рассмотрим распределение напряжений по толщине стенки в сечении, например 1-1. Для этого проанализируем формулы 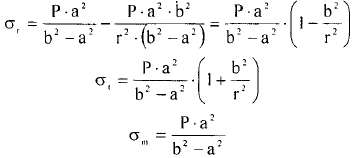 Как видно, σr, σt для какого то конкретного аппарата (при заданных a,b,P) зависит от текущего радиуса, т.е.  А σm – постоянно по толщине стенки. Сопоставим между собой σr и σt. Для этого определим эти напряжения при r=a и r=b: а) r=a 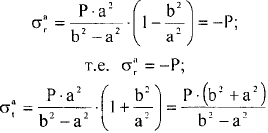 Т.к. (b2+a2)>( b2-a2), то при r=a σt>0 и | σtа|>| σrа|, а меридиональное напряжение равно 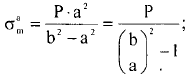 Так как для толстостенных аппаратов Где β – коэффициент толстостенности, то, например при β=1,5, значение меридионального напряжение при r=a составит Таким образом, анализ напряжений, действующих на внутр. Волокнах, показывает, что б) r=b,  Чтобы определить на сколько отличаются тангенциальные напряжения при r=b и r=a найдём величину σtа - σtb: Таким образом, σtа - σtb = Р. Сравнение т.ж. показывает, что σtb> σmb. Строим эпюры  Таким образом, анализ изменения этих напряжений по толщине стенки показывает, что по абсолютному значению σt и σr максимальны на внутренних волокнах, σm – постоянны по S. При давлении Р, не изменяющемся вдоль меридиана (равномерном газовом давлении), эпюры напряжений одинаковы по высоте аппарата. Анализ распределения напряжений по толщине стенки показывает, что наиболее опасные – внутренние волокна. Для них условие прочности по 3 теории прочности может быть записано след.образом: Т.к. σtа> σmа> σrа, то σ1= σt , σ2 = σm, σ3 = σr, тогда условие прочности перепишется в виде σt - σr ≤ [σ] при r = a При r = а напряжения σt и σr соответственно равны Подставив эти значения в условие прочности, получим Заменив в последней формуле b на Dн/2 и а на Dв/2, получим 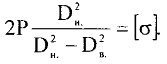 Произведя ряд преобразований: 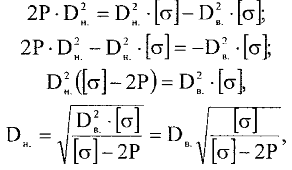 Получим уравнение для расчёта толщины стенки толстостенного аппарата: 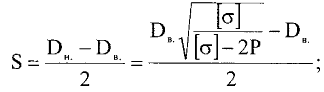  9. Толщина стенки однослойного (монолитного) цилиндрического сосуда, находящегося под воздействием внутреннего избыточного давления (без вывода). Анализ формулы. Методы повышения несущей способности однослойных сосудов. Условие оптимальности. Толщина стенки многослойных сосудов. 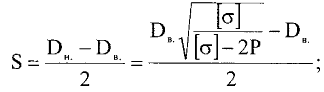  Для толстостенных сосудов давление P достигает больших значений, соизмеримых с допускаемыми напряжениями, и при значениях 2P> 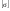 , уравнение не имеет решения. Необходимо повысить несущую способность одним из нижеприведенных способов. , уравнение не имеет решения. Необходимо повысить несущую способность одним из нижеприведенных способов.Многослойные цилиндры создаются путем надевания одного цилиндра на другой в горячем состоянии, с натягом. Каждый последующий цилиндр имеет внутренний радиус несколько меньше внешнего радиуса цилиндра, на который он одет. Разница между обоими радиусами составляет натяг. Охлаждаясь, внешний цилиндр, надетый на внутренний с натягом в горячем состоянии, сжимает внутренний цилиндр. На поверхности раздела двух цилиндров возникает так называемое монтажное давление - Рм, под действием которого внутренний цилиндр сжимается, а внешний - растягивается, т.е. оболочка 1 нагружена наруж. давлением, а 2-внутренним. Анализ формул и эпюр распределения напряжений по толщине стенки толстостенного аппарата показывает что: наиболее нагружены внутренние волокна, т.к  и и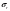 имеют максимальные значения; напряжения по мере удаления от внутренней поверхности снижаются весьма быстро. имеют максимальные значения; напряжения по мере удаления от внутренней поверхности снижаются весьма быстро.Увеличить несущую способность это значит сконструировать таким образом чтобы при меньшей толщине стенки аппарат мог воспринимать большую нагрузку (давление). Это может быть достигнуто путем: а) уменьшения напряжений на внутренних волокнах; и б) более равномерного распределения их по толщине стенки. Методы увеличения несущей способности: 1) создание многослойных сосудов; 2) метод автофреттирования (автокрепления, самокрепления). Автофреттирование – использование остаточных деформаций для повышения прочности однослойных сосудов. При повышении внутреннего давления однослойного цилиндра напряжения возврастают. Если напряжения на внутренних слоях будут превосходить предел текучести материал начнет течь. А слои где напряжения ниже предела текучести останутся упругими. Если не доводя до разрыва будем уменьшать давление, та часть стенки которая пришла в пластическое состояние будет иметь остаточные деформации и ее радиус будет стремиться оставаться несколько больше первоначального. Наружные слои будут стремиться вернуться в первоначальное состояние (т.к упругие), но им будут препятствовать внутренние слои. Поэтому внешние слои останутся, немного растянутыми, т. е наблюдается картина надевания сосудов друг на друга с натягом и создании монтажного давления. Если после этого нагрузить сосуд рабочим давлением напряжения, возникающие от него будут складываться алгебраически с напряжениями, возникающими при автофреттаже. В результате более равномерное распределение напряжений. Сосуд считается спроектированным оптимально, если эквивалентные напряжения на внутренних радиусах каждого цилиндра равны между собой, т.е. равномерное распределение напряжений по толщине стенки. Для двухслойного сосуда условие оптимальности: 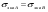 . Гадолин определил: . Гадолин определил:  с-радиус сопряжения; а- внутренний радиус, b- наружный радиус. с-радиус сопряжения; а- внутренний радиус, b- наружный радиус.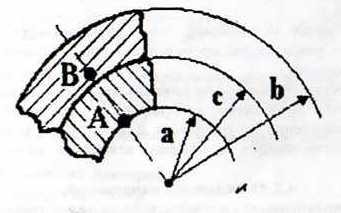 Соотношение Гадолина справедливо если двухслойный цилиндр изготовлен из одного материала. Если слоев больше то условие Гадолина примет вид: 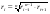 n-число слоев, n-число слоев, 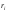 - радиус сопряжения i-го слоя. - радиус сопряжения i-го слоя.Толщина стенки по 3 теории прочности: 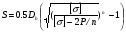 По 4: 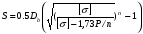 Для двухслойных сосудов при расчете напряжений может применятся метод, согласно которому отдельно определяются напряжения от внутреннего давления для монососуда и от монтажного давления для двухслойного, а затем путем суммирования эпюр, находятся напряжения в составном сосуде.при числе слоев более 2 этот метод применять трудно и напряжения могут быть найдены по методу начальных параметров. 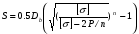 - для многослойного (n-число слоев). - для многослойного (n-число слоев).10. Механические колебания валов. Критическая скорость вала с одним грузом (анализ формулы динамического прогиба). Условие виброустойчивости. Явление самоцентрирования. Колебаниями (колебательным движением) называют все виды движения (или изменения состояния), которые обладают какой-либо степенью повторяемости во времени. Колебания наз-ся периодическими, если значения величин, изменяющиеся в процессе колебаний, повторяются через равные промежутки времени. Колебания характеризуются несколькими параметрами, среди которых: период, частота, циклическая (круговая) частота. Различают колебания: - материальных объектов, все три измерения которых сравнимы между собой (фундаменты машин); - оболочек (тонкостенных цилиндров, сфер) и тонкостенных пластин, т.е. тел, два измерения которых значительны по сравнению с третьим (толщиной); - стержней, т.е. тел, в которых одно измерение (длина) весьма велико по сравнению с двумя другими. Валы относятся к стержням. Различают 3 типа колебания стержней: 1) продольные колебания – сечения стержней колеблются вдоль оси стержня около положения равновесия; 2) поперечные колебания или колебания изгиба – сечения стержня смещаются нормально к его оси поочередно по одну и другую сторону от положения равновесия, поворачиваясь при этом вокруг своих нейтральных осей; 3) крутильные колебания – сечения стержня поворачиваются на некоторый угол φ, оставаясь в своей плоскости, вокруг оси стержня попеременно в одну и другую стороны. Валы машин обычно совершают поперечные колебания. Величина динамического прогиба: 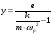 где 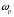 - рабочая угловая скорость вращения вала; - рабочая угловая скорость вращения вала;k – коэффициент жесткости вала, то есть сила, вызывающая прогиб, равный единице. Угловая скорость собственных (свободных) колебаний невесомого вала с одной сосредоточенной массой: 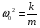 Тогда: Тогда: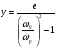 Угловая скорость колебаний вала, при которой прогибы значительно возрастают и вращающиеся валы становятся динамически неустойчивыми, наз-ся критической ωкр. Из уравнения видно, что для вала с одним диском ωкр равна угловой скорости свободных колебаний: 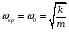 Эту формулу обычно приводят к более удобному для расчета виду: 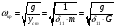 где  - единичный прогиб или коэффициент влияния, то есть Yст от единичной поперечной силы; - единичный прогиб или коэффициент влияния, то есть Yст от единичной поперечной силы;g – ускорение свободного падения; Ycт- статический прогиб вала под массой m=G/g Следовательно, вращение вала с рабочей скоростью, равной критической или близкой к ней, недопустимо. Рабочая скорость должна быть либо больше (для гибких валов), либо меньше (для жестких валов) критической угловой скорости. Рекомендуется принимать: - для жестких валов: ωр 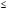 0,7ωкр 0,7ωкр- для гибких валов: ωр>1,3ωкр Эти условия наз-ся условиями виброустойчивости валов. В зависимости от соотношения рабочей угловой скорости ωр и критической ωкр: - жесткие при ωр< ωкр; - гибкие при ωр> ωкр: Величина динамического прогиба:  Если величина 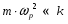 , а это происходит, когда , а это происходит, когда 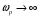 , то , то 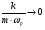 , тогда получаем, что y= -e , тогда получаем, что y= -eто есть при  прогиб значительно уменьшается и стремится к величине эксцентриситета «e», а точки вала под нагрузками располагаются на оси вращения. прогиб значительно уменьшается и стремится к величине эксцентриситета «e», а точки вала под нагрузками располагаются на оси вращения. Вал, как говорят, самоцентрируется. Практически речь идет не о беско нечной скорости, а о скорости, значительно превышающей критическую. Подобное самоцентрирование валов крайней важно, тк при этом прогиб, а с ним и центробежные силы относительно оси вращения, уменьшаются: 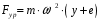 будет же: 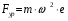 Вал работает спокойно, прогибы стремятся к нулю и напряжения изгиба снижаются. Поэтому, когда речь идет о быстровращающихся валах, целесообразно работать на гибких валах. |
