Расшифровка маркировки, область применения (агрессивное воздействие среды, давление, температура)
 Скачать 7.79 Mb. Скачать 7.79 Mb.
|
|
11.Особенности расчета валов с несколькими массами. Понятие о точном методе расчета критических скоростей. Приближенные методы. Если вал представляет собой многомассовую систему, состоящую, например, из nсосредоточенных масс, то он имеет n собственных угловых скоростей (частот) и, в простейшем случае, n критических скоростей. Следовательно, задача определения критической скорости вала, нагруженного несколькими сосредоточенными массами, сводится к определению частот его собственных колебаний. Если сосредоточенных масс более двух, то точное решение такой задачи очень сложно. В практических случаях часто приходится сталкиваться с необходимостью определения частоты собственных колебаний систем, имеющих несколько степеней свободы. Представим балку, находящуюся под действием нескольких сил P1; P2; P3 … при 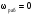 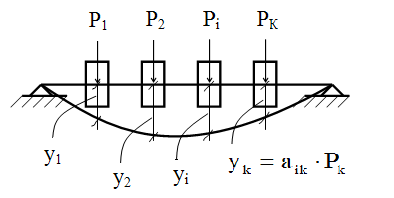 Рисунок 9.10 – Схема балки под действием нескольких сил Перемещение при деформации балки в месте приложения и по направлению действия каждой из этих сил обозначим y1; y2; yi; yk. Пусть   Рисунок 9.11 – Схема единичного прогиба балки Из курса сопротивления материалов известно, что прогиб По аналогии прогибы в направлении действия сил  (9.32) (9.32)Точный метод определения критических частот вала. Рассмотрим вал с двумя дисками при  Рисунок 9.12 – Схема прогиба вала с двумя грузами при При вращении на вал действуют центробежные силы В соответствии с (9.32) можно записать  (9.35) (9.35)Подставим значение сил в (9.35)  (9.36) (9.36)Раскроем скобки и систему уравнений (9.36) перепишем следующим образом:  (9.37) (9.37)Сгруппируем и введем обозначение членов уравнения  (9.38) (9.38)Полученные уравнения представляют систему из двух неоднородных уравнений с двумя неизвестными. Эти уравнения удобно решить с помощью определителей. Каждое решение может быть представлено в виде дроби, знаменателем которой является определитель, составленный из коэффициентов при неизвестных, а числитель – тот же определитель, в котором коэффициенты при искомом неизвестном заменены свободными членами A1 и A2 , то есть  ; ;  . (9.40) . (9.40)Как было сказано ранее резонанс наступает тогда, когда прогибы стремятся к бесконечности, то есть  . (9.41) . (9.41)Раскроем определитель Полагая Решение этого квадратного уравнения имеет вид  , (9.45) , (9.45)При При Когда число масс, то есть число степеней свободы 4 и больше, то решить систему уравнений без ЭВМ невозможно ( Приближенные методы определения критической угловой скорости вала с несколькими сосредоточенными массами На практике обычно в таких случаях используются приближенные методы расчета критических угловых скоростей  (8) (8)Валы быстроходных машин обычно проектируются как жесткие, реже применяются гибкие валы, работающие между первой и второй критическими скоростями Рисунок 10. 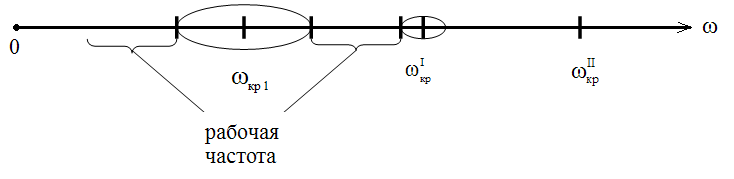 Метод Донкерли В методе Донкерли используется принцип независимости воздействия отдельных масс на колебания вала (принцип суперпозиции). Формула Донкерли, по которой определяется наименьшее возможное значение основной частоты  , (9) , (9)где  – критическая угловая скорость вала, когда он нагружен только одним грузом массой mi; – критическая угловая скорость вала, когда он нагружен только одним грузом массой mi;i – число масс на валу. Метод Донкерли дает заниженное значение 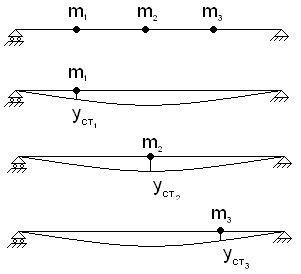  Рисунок 11 – Расчетная схема и первая (низшая) критическая скорость вала, нагруженного тремя сосредоточенными массами, определяемая по методу Донкерли. по таблице для однопролетного и консольного валов на неподатливых подшипниках представлены значения коэффициентов Энергетический метод Релея В основе энергетического метода лежит принцип постоянства энергии, согласно которому максимальная потенциальная энергия деформации при вращении вала После раскрытия данного равенства получено одно из выражений для расчета нижней критической частоты  , (11) , (11)где  (12) (12) Рисунок 12- Расчетная схема и первая (низшая) критическая скорость вала, нагруженного тремя сосредоточенными массами (метод Релея). Критическая частота, получаемая по методу Релея, всегда выше действительной частоты ( т.е частоты, найденной точным методом).. Действительная частота находится между частотой, определенной по формуле Донкерли Рассмотренные выше методы определения первой критической скорости вращения валов, в которых прогибы рассчитываются аналитически, просты и удобны в случае валов постоянного сечения и с небольшим числом нагрузок. При расчете балок переменного сечения со многими сосредоточенными массами Методы в этом случае называются графо-аналитическими. В литературе приводится еще ряд методов для расчета валов переменного сечения. В практике химического машиностроения получил распространение так называемый метод приведения, основанный на исследованиях академика Ю. А. Шиманского /4/, который является достаточно простым, точным и универсальным, так как может быть применен как при расчете валов переменного, так и постоянного сечения, с одной или несколькими сосредоточенными массами, с учетом или без учета массы вала. 12. Колебания валов. Гироскопический эффект. Влияние различных факторов на критическую скорость Колебаниями (колебательным движением) называют все виды движения (или изменения состояния), которые обладают какой-либо степенью повторяемости во времени. Колебания называются периодическими, если значения величин, изменяющиеся в процессе колебаний, повторяются через равные промежутки времени. Колебания характеризуются несколькими параметрами, среди которых: период, частота, циклическая (круговая) частота. При вращении валы совершают колебания, которые состоят из суммы двух колебаний – вынужденных, вызванных периодически изменяющейся центробежной силой 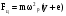 , приложенной в центре масс „с” (рисунок 6), и свободных, которые возникают под влиянием импульса, сообщенного валу этой же силой. Причиной появления силы , приложенной в центре масс „с” (рисунок 6), и свободных, которые возникают под влиянием импульса, сообщенного валу этой же силой. Причиной появления силы 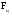 является остаточный дисбаланс (эксцентриситет) „е”, то есть смещение центра масс деталей (в данном случае в качестве детали выступает диск - это может быть, например, рабочее колесо центробежного насоса) от геометрической оси вращения вала, который существует всегда, как бы точно не изготавливались вращающиеся детали (валы, диски, роторы и так далее) и как бы тщательно они не были сбалансированы. Силу является остаточный дисбаланс (эксцентриситет) „е”, то есть смещение центра масс деталей (в данном случае в качестве детали выступает диск - это может быть, например, рабочее колесо центробежного насоса) от геометрической оси вращения вала, который существует всегда, как бы точно не изготавливались вращающиеся детали (валы, диски, роторы и так далее) и как бы тщательно они не были сбалансированы. Силу 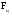 уравновешивает противоположно направленная и приложенная к точке „0” крепления диска массой „m” к валу сила упругости уравновешивает противоположно направленная и приложенная к точке „0” крепления диска массой „m” к валу сила упругости 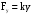 . Из условия равновесия сил на ось у получим . Из условия равновесия сил на ось у получим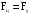 , (1) , (1)Подставив значение 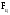 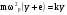 , (2) , (2)где 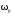 – рабочая угловая скорость вращения вала; – рабочая угловая скорость вращения вала;y – динамический прогиб вала под массой m; k – коэффициент жесткости вала, то есть сила, вызывающая прогиб, равный единице. Из уравнения (2) находим величину динамического прогиба: 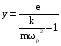 . (3) . (3)Ранее было получено, что величина 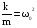 , где , где 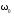 – угловая скорость собственных (свободных) колебаний невесомого вала с одной сосредоточенной массой (без учета сил трения), тогда: – угловая скорость собственных (свободных) колебаний невесомого вала с одной сосредоточенной массой (без учета сил трения), тогда: . (4) . (4)Анализ уравнения (4) показывает, что при увеличении рабочей скорости и приближении ее к частоте собственных колебаний вала, т.е. при 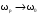 прогиб вала (амплитуда) неограниченно возрастает и стремиться к бесконечности, т.е. прогиб вала (амплитуда) неограниченно возрастает и стремиться к бесконечности, т.е. 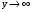 . . Случай совпадения частоты вынужденных колебаний с частотой свободных колебаний называется резонансом. В действительных условиях при наличии трения амплитуды при резонансе остаются конечными, но достигают значительной величины. Резонанс представляет собой большую опасность для конструкции и его следует избегать. Одна из основных задач расчета конструкции на вибрацию состоит в определении собственных частот колебаний и выявлении опасных резонансных частот. Резонансы обычно устраняют изменением собственной частоты системы; в ряде случаев оказывается возможным изменить частоту возбуждающей силы. Угловая скорость колебаний вала, при которой прогибы значительно возрастают и вращающиеся валы становятся динамически неустойчивыми, называется критической – 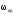 . Из уравнения (4) видно, что для вала с одним диском . Из уравнения (4) видно, что для вала с одним диском 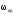 равна угловой скорости собственных колебаний, то есть: равна угловой скорости собственных колебаний, то есть: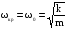 . (5) . (5)Обычно формулу (5) приводят к более удобному для расчета виду: 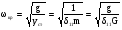 , (6) , (6)где 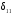 – единичный прогиб или коэффициент влияния, то есть – единичный прогиб или коэффициент влияния, то есть 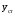 от единичной поперечной силы; от единичной поперечной силы;g – ускорение свободного падения; 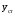 – статический прогиб вала под массой – статический прогиб вала под массой 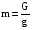 ; ;G – вес вала. Из сказанного очевидно, что вращение вала с рабочей скоростью, равной критической или близкой к ней, недопустимо. Рабочая скорость должна быть либо больше (для гибких валов), либо меньше (для жестких) критической угловой скорости. Рекомендуется принимать 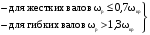 (7) (7) Условия (7) называются условиями виброустойчивости валов. |
