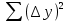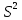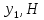диссертация. Разработка методов расчёта внутритрубных элементов для локального ремонта подводных переходов трубопроводов
 Скачать 4.08 Mb. Скачать 4.08 Mb.
|
|
2.7.3. Экспериментальное исследование деформации модели внутренней гильзы из материала с эффектом памяти формы Экспериментальная установка (рис.2.23) предназначена для исследования формообразования и изменения геометрических параметров в  Рис.2.23. Общий вид экспериментальной установки процессе деформации ремонтного кольца из NiTi в «плоской модели трубопровода» [93,126]. Установка представляет собой плиту ДСП, на которой крепятся датчики, измерительное оборудование и «плоская модель трубопровода». При проведении эксперимента использовались следующие приборы: 1) тензодатчик LPS (контроль данных производился при помощи прецизионного датчика «Микросим 06-А»); 2) -прецизионный тензоизмеритель МО600-А «Микросим 06А»; 3) -датчик перемещения, цена деления 0,01 мм;  Рис. 2.24. Тензодатчик с упорными осями. 4) проволока NiTi сплава с памятью формы, температура срабатывания 41-470С, диаметр 2 мм, химический состав - никель 55,2%, титан 44,8%, углерод 0,037%, кислород 0,10%, азот 0,009%, водород 0,0072% (приложение 2.2). Все измерения проводились при температуре 30 градусов Цельсия. Стенд выполнен из двух параллельных дисков из оргстекла, между которыми устанавливается модель гильзы из СПФ. Нижнее стекло является основой и имеет форму цельного диска толщиной 5 мм и диаметром 530 мм, среднее кольцо имеет толщину 2 мм и выполнено в виде секторов, расчлененных между собой и закрепленных с шагом в 2 мм. Верхний диск фиксирует испытуемый образец и представляет собой кольцо из оргстекла толщиной 2 мм с внешним и внутренним диаметрами 530 мм и 380 мм соответственно. В этой же последовательности диски из оргстекла соединены друг с другом. 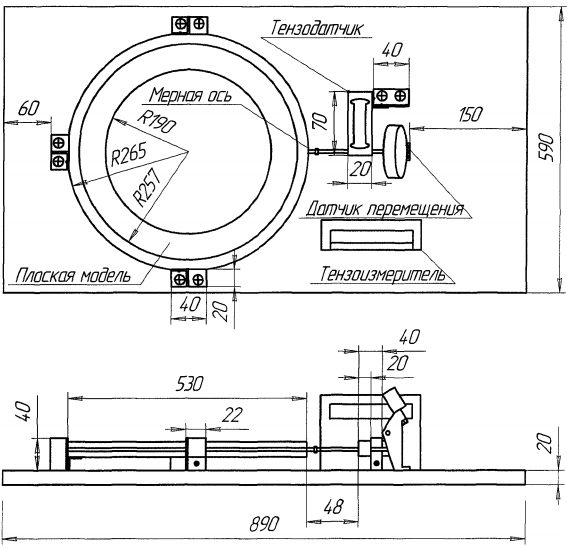 Рис 2.25. Схема экспериментальной установки Конструкция установки обеспечивает не только прямой доступ к испытуемому образцу, но и его визуальное наблюдение. Датчик усилий установлен так, чтобы измерительная ось, имеющая ход в 30 мм, входила в измерительное отверстие на плоской модели перпендикулярно касательной к исследуемому образцу (рис. 2.24). При этом диск модели вращается вокруг своей оси. С противоположной стороны от датчика усилий установлен датчик перемещений, в который упирается ось, вкручиваемая в тензодатчик и имеющая диапазон регулировки 28 мм. Вторичный прибор тензодатчика имеет подставку и может выноситься со станины. Для проведения экспериментов была использована проволока из сплава с памятью формы N1X1 с температурой мартенситного превращения от 41 до 47 V . Образец изготавливался из проволоки круглого сечения, что позволило не учитывать деформации кручения. На первом этапе происходит подготовка образцов, т.е. придание ремонтному элементу конечной формы. Для этого сплав подвергается термической обработке и деформируется. Контроль температуры происходит при помощи электронного термометра, погрешность измерений которого составляет 0,1 градусов Цельсия. На втором этапе эксперимента при низких температурах (ниже нуля) модель ремонтной вставки деформируется до размера меньше внутреннего диаметра трубопровода. Количество гофр при деформации элемента выбирается исходя из пороговых значений деформации и минимального размера образца в деформированном состоянии. Все изменения геометрии проволочной вставки проводятся при температуре, обеспечивающей протекание полного мартенситного превращения с целью обеспечения полного восстановления исходной формы, заданной во время проведения первого этапа эксперимента. При деформации образцов для «плоской модели трубопровода» использовалось вспомогательное устройство, представляющее собой станину с установленными на ней упорами, при помощи которых задавался профиль исследуемого образца. При гофрировании ремонтного элемента деформация в любой его точке не превышала 8 %, что обеспечивало восстановление первоначальной формы СПФ. Соотношение диаметров ремонтной вставки в развернутом и гофрированном состоянии определялось экспериментально или расчётным путём доводилось до значения 1,8. На следующем этапе проволочная конструкция устанавливается между дисками оргстекла, моделируя работу ремонтной вставки во внутренней полости трубопровода. При температуре воды 41-48 градусов Цельсия, плоская модель погружается в ванну. Такая схема позволяет равномерно и одновременно нагреть образец до необходимой температуры. При достижении сплавом температуры срабатывания, проволочная модель начинает расправляться. В первую очередь касание внутренней полости ремонтируемого участка происходит в точках А (рис.2.2б) Создав себе опорную поверхность образец переходит в промежуточное состояние, при котором кривизна между точками касания меняет знак. Пройдя точку, характеризующую бесконечную кривизну, испытуемый элемент упруго «срабатывает» по всему контуру ремонтируемой поверхности. 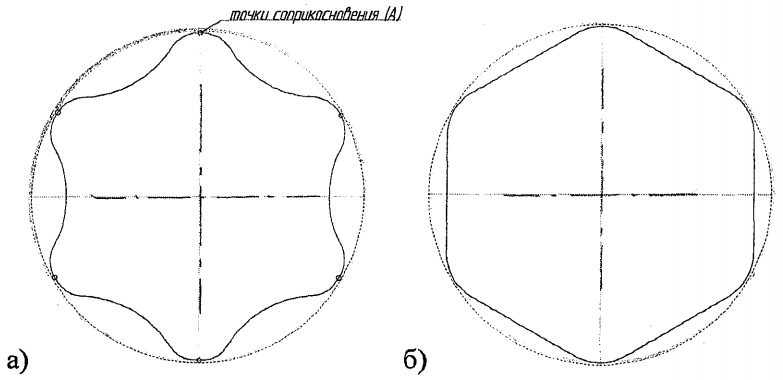 Рис. 2.26 Схема раскрытия ремонтного элемента Далее «плоская модель» извлекается из ванны и устанавливается на «основу» экспериментальной установки. Создав необходимый температурный режим, проводится измерение усилий прижатия проволоки к внутренней поверхности «плоской модели» по всему её контуру. Замеры проводятся по всему контуру плоской модели. Датчик перемещений устанавливается в центре плоской модели, на основании обеспечивающем его вращение по всем контуру. Усилие прижатия измеряется в каждой точке ввода мерного штока. Полученные данные заносятся в программный комплекс Microsoft Excel (Табл. 2.8.) и обрабатываются в программном комплексе Statistica. Для проверки воспроизводимости опытов проведено несколько серий параллельных опытов. Приняты следующие обозначения: перемещение участка проволоки, к которому прикладывается усилие-х; результаты измерений - у. Опыт проводился в трех повторностях. План и результаты эксперимента сведены в таблицу 2.3. Усилия замерялись в точках, соответствующих участкам «выпуклости» гофрированной проволоки. После проведения опыта в табл. 2.3 занесены его результаты (уь у г и Уз.). Обработка результатов проводилась в следующей последовательности: 1. Среднеарифметическое из m повторностей 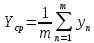 (2.32) (2.32)2. Квадраты отклонений 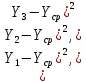 3. По каждой строчке плана сумма квадратов отклонений: 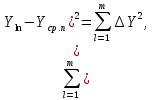 (2.33) (2.33)4. Построчная дисперсия 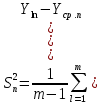 (2.34) (2.34)5. Сумма построчных дисперсий 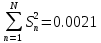 (2.35) (2.35)6. Расчетное значение критерия Кохрена Таблица 2.3 Эксперимент для проверки воспроизводимости опытов
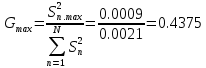 (2.36) (2.36)Для определения табличного значения критерия Кохрена найдем число степеней свободы: 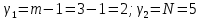 Из табл. 2.4. 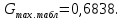 Условие Условие 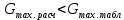 (0,4375<0,6838) выполняется, поэтому опыты можно считать воспроизводимыми. (0,4375<0,6838) выполняется, поэтому опыты можно считать воспроизводимыми.
Значение G-критерия (Кохрена) для уровня значимости α=0,05 чисел степеней свободы 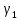 и и  Для проверки гипотезы нормального распределения поставлена серия из 20 опытов для значений 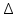 =5 мм. Полученные значения перемещений точки проволоки, к которой прикладывалась нагрузка, приведена в табл. 2.8. =5 мм. Полученные значения перемещений точки проволоки, к которой прикладывалась нагрузка, приведена в табл. 2.8.Таблица 2.5 Вычисление выборочных характеристик
Среднее значение выборки 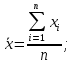 (2.37) (2.37)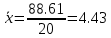 Дисперсия эмпирического распределения (второй центральный момент) 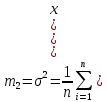 (2.38) (2.38)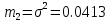 (см. табл. 2.5.). (см. табл. 2.5.).Несмещенная оценка (дисперсия теоретического распределения) 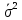 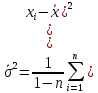 (2.39) (2.39)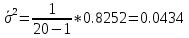 Выборочные среднеквадратические отклонения 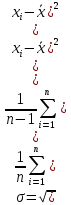 (2.40) (2.40)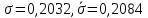 Первый центральный момент 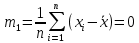 Третий центральный момент 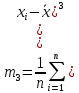 Четвертый центральный момент 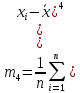 Коэффициент вариации 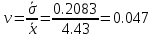 (2.47) (2.47)Систематических погрешностей выявлено не было. При исключении грубых погрешностей использовался метод вычисления максимального относительного отклонения (так как объем выборки небольшого объема п меньше 25). 1. Наиболее отклоняющееся от среднего значение 4,87. Тогда наибольшее отклонение 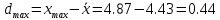 2. Статистика 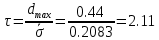 3. Квантиль распределения статистики т при уровне значимости 0,05 для п=20 равен 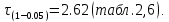 Значение 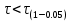 (2,11<2.62) поэтому значение 4,87 можно оставить для дальнейшей обработки данных. (2,11<2.62) поэтому значение 4,87 можно оставить для дальнейшей обработки данных.Проверка гипотезы о нормальном распределении случайных погрешностей эксперимента проведена в программном комплексе 8ТАТ18Т1СА с помощью критерия Колмогорова-Смирнова, а также по критерию Пирсона. Гистограмма частот приведена на рис. 2.27. На основе проведенного анализа можно сделать вывод, что случайные ошибки эксперимента подчиняются нормальному закону распределения. 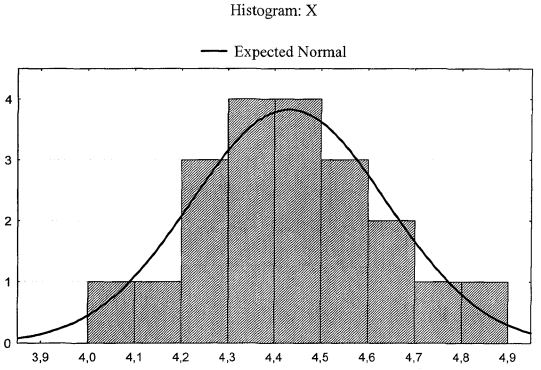 X <= Category Boundary Рис. 2.27. Гистограмма частот Таблица 2.6 Квантили распределения максимального относительного отклонения 
Для определения количества повторностей измерений зададимся надежностью результатов опытов α=0,95 и допустимой ошибкой 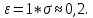 Тогда необходимое количество повторностей опытов примем равным 7 (табл. 2.7.). Тогда необходимое количество повторностей опытов примем равным 7 (табл. 2.7.).Таблица 2.5 Необходимое количество повторностей
По данным таблицы строится диаграмма, описывающая поведение проволочного элемента при его деформации на стенде «плоская модель» по критерию внутреннего прогиба (рис.2.28.). На диаграмме показаны значения отклонений при потере устойчивости кольца для всех сорока восьми положений. На графике явно выражен перегиб в области нулевой кривизны, которая формируется на расстоянии 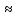 7 миллиметров от начального положения кольца. 7 миллиметров от начального положения кольца. График средних значений показан на рис.2.29. Как видно из графиков усилий, возникающих при деформации кольца, достаточно для установки его в проектное положение даже без учёта давления перекачиваемого продукта, которое в реальных условиях сопоставимо с усилиями, возникающими при деформации гильзы. Данные эксперимента заносятся таблично в программный комплекс Microsoft Excel для обработки и построения графических зависимостей. Таблица 2.8
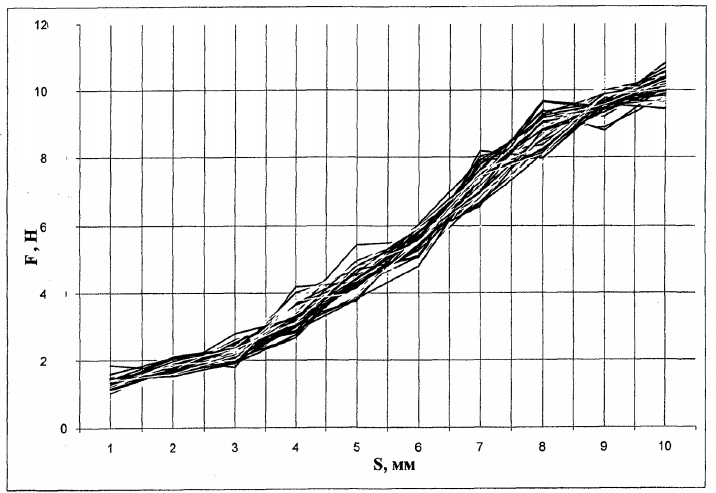 Рис. 2.28 Усилие деформации элемента из СПФ 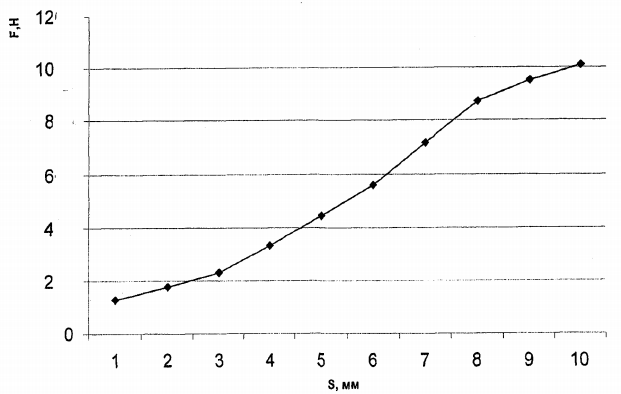 Рис. 2.29 Усилие деформации элемента из СПФ В результате экспериментов было выявлено, что распределение усилий по внутренней поверхности неравномерно, а увеличение нормального давления происходит в точках с «первоначальным касанием проволочного элемента. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||